10.6: Параметричні рівняння
- Page ID
- 59372
- Параметризувати криву.
- Усунути параметр.
- Знайдіть прямокутне рівняння для кривої, визначеної параметрично.
- Знайти параметричні рівняння для кривих, визначених прямокутними рівняннями.
Розглянемо шлях, яким слідує місяць, коли він обертається навколо планети, яка одночасно обертається навколо Сонця, як показано на малюнку\(\PageIndex{1}\). У будь-який момент Місяць розташовується в певному місці щодо планети. Але як нам писати і вирішувати рівняння положення Місяця, коли відстань від планети, швидкість місячної орбіти навколо планети, і швидкість обертання навколо Сонця все невідомі? Ми можемо вирішити тільки для однієї змінної за раз.
У цьому розділі ми розглянемо множини рівнянь, заданих\(x(t)\) і\(y(t)\)\(t\) де незалежна змінна часу. Ми можемо використовувати ці параметричні рівняння в ряді застосувань, коли ми шукаємо не тільки певну позицію, але і напрямок руху. Коли ми простежуємо послідовні значення\(t\), орієнтація кривої стає зрозумілою. Це одна з основних переваг використання параметричних рівнянь: ми можемо простежити рух об'єкта по шляху відповідно до часу. Ми починаємо цей розділ з погляду на основні складові параметричних рівнянь і те, що означає параметризація кривої. Потім ми дізнаємося, як усунути параметр, перевести рівняння кривої, визначеної параметрично, в прямокутні рівняння, і знайдемо параметричні рівняння для кривих, визначених прямокутними рівняннями.
Параметризація кривої
Коли об'єкт рухається вздовж кривої - або криволінійного шляху - у заданому напрямку та за заданий проміжок часу, положення об'єкта у площині задається координатою\(x\) - та координатою.\(y\) Однак обидва\(x\) і\(y\) змінюються з часом і так є функціями часу. З цієї причини додаємо ще одну змінну, параметр, від якої обидві\(x\) і\(y\) є залежними функціями. У прикладі в розділі відкривачка параметром є час,\(t\). \(x\)Положення Місяця в часі\(t\), представлено як функція\(x(t)\), а\(y\) положення Місяця в часі\(t\), представляється як функція\(y(t)\). Разом\(x(t)\) і\(y(t)\) називаються параметричними рівняннями, і генерують впорядковану пару\((x(t), y(t))\). Параметричні рівняння в першу чергу описують рух і напрямок.
Коли ми параметризуємо криву, ми переводимо єдине рівняння в двох змінних, таких як\(x\) і\(y\), в еквівалентну пару рівнянь у трьох змінних,\(x\),\(y\), і\(t\). Однією з причин, чому ми параметризуємо криву, є те, що параметричні рівняння дають більше інформації: зокрема, напрямок руху об'єкта з плином часу.
Коли ми графуємо параметричні рівняння, ми можемо спостерігати індивідуальну поведінку\(x\) і з\(y\). Існує ряд фігур, які не можуть бути представлені у формі\(y=f(x)\), а це означає, що вони не є функціями. Для прикладу розглянемо графік кола, заданий як\(r^2=x^2+y^2\). Розв'язування для\(y\) дає\(y=\pm \sqrt{r^2−x^2}\), або два рівняння:\(y_1=\sqrt{r^2−x^2}\) і\(y_2=−\sqrt{r^2−x^2}\). Якщо ми\(y_1\) графуємо і\(y_2\) разом, графік не пройде тест вертикальної лінії, як показано на малюнку\(\PageIndex{2}\). Таким чином, рівняння для графа кола не є функцією.
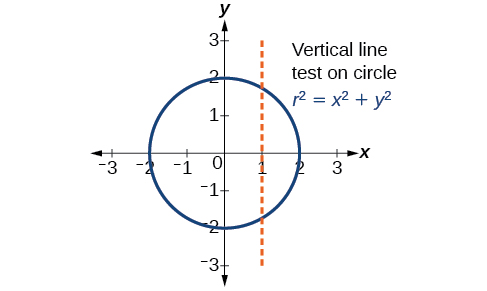
Однак, якби ми графували кожне рівняння самостійно, кожне з них пройшло б тест вертикальної лінії і, отже, представляло б функцію. У деяких випадках концепція розбиття рівняння для кола на дві функції схожа на концепцію створення параметричних рівнянь, оскільки ми використовуємо дві функції для отримання нефункції. Це стане зрозуміліше в міру просування вперед.
Припустимо,\(t\) це число на проміжку,\(I\). Множина впорядкованих пар\((x(t), y(t))\), де\(x=f(t)\) і\(y=g(t)\), утворює плоску криву на основі параметра\(t\). Рівняння\(x=f(t)\) і\(y=g(t)\) є параметричними рівняннями.
Параметризуємо криву\(y=x^2−1\) пускання\(x(t)=t\). Графік обох рівнянь.
Рішення
Якщо\(x(t)=t\), то знайти\(y(t)\) замінюємо змінну на\(x\) вираз, заданий в\(x(t)\). Іншими словами,\(y(t)=t^2−1\) .Складіть таблицю значень, схожу на Таблицю\(\PageIndex{1}\), і намалюйте графік.
| \(t\) | \(x(t)\) | \(y(t)\) |
|---|---|---|
| \ (t\) ">\(−4\) | \ (x (t)\) ">\(−4\) | \ (y (t)\) ">\(y(−4)={(−4)}^2−1=15\) |
| \ (t\) ">\(−3\) | \ (x (t)\) ">\(−3\) | \ (y (t)\) ">\(y(−3)={(−3)}^2−1=8\) |
| \ (t\) ">\(−2\) | \ (x (t)\) ">\(−2\) | \ (y (t)\) ">\(y(−2)={(−2)}^2−1=3\) |
| \ (t\) ">\(−1\) | \ (x (t)\) ">\(−1\) | \ (y (t)\) ">\(y(−1)={(−1)}^2−1=0\) |
| \ (t\) ">\(0\) | \ (x (t)\) ">\(0\) | \ (y (t)\) ">\(y(0)={(0)}^2−1=−1\) |
| \ (t\) ">\(1\) | \ (x (t)\) ">\(1\) | \ (y (t)\) ">\(y(1)={(1)}^2−1=0\) |
| \ (t\) ">\(2\) | \ (x (t)\) ">\(2\) | \ (y (t)\) ">\(y(2)={(2)}^2−1=3\) |
| \ (t\) ">\(3\) | \ (x (t)\) ">\(3\) | \ (y (t)\) ">\(y(3)={(3)}^2−1=8\) |
| \ (t\) ">\(4\) | \ (x (t)\) ">\(4\) | \ (y (t)\) ">\(y(4)={(4)}^2−1=15\) |
Див. Графіки на рисунку\(\PageIndex{3}\). Це може бути корисно використовувати функцію TRACE графічного калькулятора, щоб побачити, як точки генеруються у міру\(t\) збільшення.
Аналіз
Стрілки вказують напрямок, в якому формується крива. Зверніть увагу, що крива ідентична кривій\(y=x^2−1\).
Побудуйте таблицю значень і побудуйте параметричні рівняння:\(x(t)=t−3\),\(y(t)=2t+4\);\(−1≤t≤2\).
- Відповідь
-
\(t\) \(x(t)\) \(y(t)\) \ (t\) ">\(-1\) \ (x (t)\) ">\(-4\) \ (y (t)\) ">\(2\) \ (t\) ">\(0\) \ (x (t)\) ">\(-3\) \ (y (t)\) ">\(4\) \ (t\) ">\(1\) \ (x (t)\) ">\(-2\) \ (y (t)\) ">\(6\) \ (t\) ">\(2\) \ (x (t)\) ">\(-1\) \ (y (t)\) ">\(8\) 
Малюнок\(\PageIndex{4}\)
Знайдіть пару параметричних рівнянь, які моделюють графік\(y=1−x^2\), використовуючи параметр\(x(t)=t\). Намалюйте деякі точки і накидайте графік.
Рішення
Якщо\(x(t)=t\) і\(t\) підставляємо\(x\) в\(y\) рівняння, то\(y(t)=1−t^2\). Наша пара параметричних рівнянь
\[\begin{align*} x(t) &=t \\ y(t) &= 1−t^2 \end{align*}\]
Для побудови графіків рівнянь спочатку ми будуємо таблицю значень, подібну до таблиці\(\PageIndex{2}\). Ми можемо вибирати значення навколо\(t=0\), від\(t=−3\) до\(t=3\). Значення в\(x(t)\) стовпці будуть такими ж, як і в\(t\) стовпці, тому що\(x(t)=t\). Обчисліть значення для стовпця\(y(t)\).
| \ (т) | \(x(t)=t\) | \(y(t)=1−t^2\) |
|---|---|---|
| \ (t) ">\ (−3\) | \ (x (t) =т\) ">\(−3\) | \ (y (t) =1−t^2\) ">\(y(−3)=1−{(−3)}^2=−8\) |
| \ (t) ">\ (−2\) | \ (x (t) =т\) ">\(−2\) | \ (y (t) =1−t^2\) ">\(y(−2)=1−{(−2)}^2=−3\) |
| \ (t) ">\ (−1\) | \ (x (t) =т\) ">\(−1\) | \ (y (t) =1−t^2\) ">\(y(−1)=1−{(−1)}^2=0\) |
| \ (t) ">\ (0\) | \ (x (t) =т\) ">\(0\) | \ (y (t) =1−t^2\) ">\(y(0)=1−0=1\) |
| \ (t) ">\ (1\) | \ (x (t) =т\) ">\(1\) | \ (y (t) =1−t^2\) ">\(y(1)=1−{(1)}^2=0\) |
| \ (t) ">\ (2\) | \ (x (t) =т\) ">\(2\) | \ (y (t) =1−t^2\) ">\(y(2)=1−{(2)}^2=−3\) |
| \ (t) ">\ (3\) | \ (x (t) =т\) ">\(3\) | \ (y (t) =1−t^2\) ">\(y(3)=1−{(3)}^2=−8\) |
Графік\(y=1−t^2\) являє собою параболу, звернену вниз, як показано на малюнку\(\PageIndex{5}\). Ми зіставили криву через інтервал\([−3, 3]\), показаний у вигляді суцільної лінії зі стрілками, що вказують орієнтацію кривої відповідно до\(t\). Орієнтація відноситься до контуру, що простежується вздовж кривої з точки зору збільшення значень\(t\). Оскільки ця парабола симетрична щодо лінії\(x=0\), значення значень\(x\) відображаються по осі y.
Параметризуйте криву, задану\(x=y^3−2y\).
- Відповідь
-
\(x(t)=t^3−2t\)
\(y(t)=t\)
Об'єкт рухається з постійною швидкістю по прямому шляху\((−5, 3)\)\((3, −1)\) в одній площині за чотири секунди. Координати вимірюються в метрах. Знайти параметричні рівняння для положення об'єкта.
Рішення
Параметричні рівняння - це прості лінійні вирази, але нам потрібно розглядати цю задачу поетапно. X -значення об'єкта починається з\(−5\) метрів і йде в\(3\) метри. Це означає, що відстань\(x\) змінилася на\(8\) метри в\(4\) секундах, що є швидкістю\(\dfrac{8\space m}{4\space s}\), або\(2\space m/s\). Ми можемо записати x -координата як лінійну функцію щодо часу як\(x(t)=2t−5\). У шаблоні лінійної функції\(y=mx+b\),\(2t=mx\) і\(−5=b\).
Аналогічно,\(y\) -значення об'єкта починається з\(3\) і йде до\(−1\), що є зміною відстані\(y\)\(−4\) метрів в\(4\) секундах, що є швидкістю\(\dfrac{−4\space m}{4\space s}\), або\(−1\space m/s\). Ми також можемо записати y -координату як лінійну функцію\(y(t)=−t+3\). Разом це параметричні рівняння положення об'єкта, де\(x\) і\(y\) виражаються в метрах і\(t\) представляють час:
\[\begin{align*} x(t) &= 2t−5 \\ y(t) &= −t+3 \end{align*}\]
Використовуючи ці рівняння, ми можемо побудувати таблицю значень for\(t\)\(x\), і\(y\) (див. Таблицю\(\PageIndex{3}\)). У цьому прикладі ми обмежили значення\(t\) до невід'ємних чисел. Загалом, будь-яке значення\(t\) може бути використано.
| \(t\) | \(x(t)=2t−5\) | \(y(t)=−t+3\) |
|---|---|---|
| \ (t\) ">\(0\) | \ (x (t) =2t−5\) ">\(x=2(0)−5=−5\) | \ (y (t) =−t+3\) ">\(y=−(0)+3=3\) |
| \ (t\) ">\(1\) | \ (x (t) =2t−5\) ">\(x=2(1)−5=−3\) | \ (y (t) =−t+3\) ">\(y=−(1)+3=2\) |
| \ (t\) ">\(2\) | \ (x (t) =2t−5\) ">\(x=2(2)−5=−1\) | \ (y (t) =−t+3\) ">\(y=−(2)+3=1\) |
| \ (t\) ">\(3\) | \ (x (t) =2t−5\) ">\(x=2(3)−5=1\) | \ (y (t) =−t+3\) ">\(y=−(3)+3=0\) |
| \ (t\) ">\(4\) | \ (x (t) =2t−5\) ">\(x=2(4)−5=3\) | \ (y (t) =−t+3\) ">\(y=−(4)+3=−1\) |
З цієї таблиці ми можемо створити три графіки, як показано на малюнку\(\PageIndex{6}\).
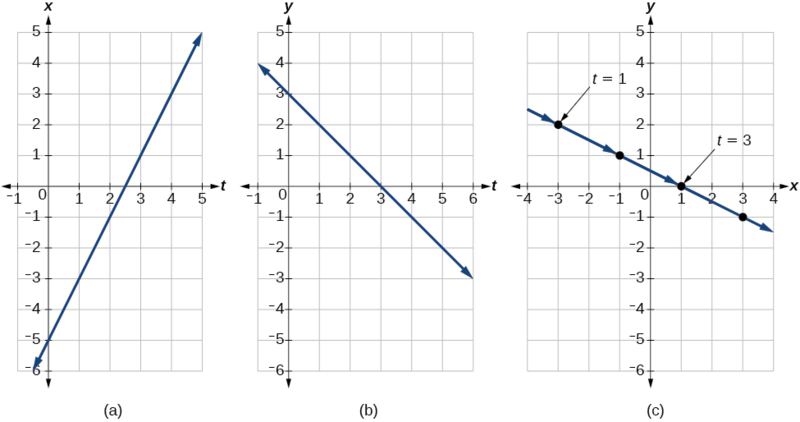
Аналіз
Знову ж таки, ми бачимо, що на малюнку\(\PageIndex{6}\) (c), коли параметр представляє час, ми можемо вказувати рух об'єкта по шляху стрілками.
Усунення параметра
У багатьох випадках ми можемо мати пару параметричних рівнянь, але виявимо, що простіше намалювати криву, якщо рівняння включає лише дві змінні, такі як\(x\) і\(y\). Усунення параметра - це метод, який може полегшити графікування деяких кривих. Однак, якщо ми стурбовані відображенням рівняння відповідно до часу, то потрібно буде вказати і орієнтацію кривої. Існують різні методи усунення параметра\(t\) з набору параметричних рівнянь; не кожен метод працює для кожного типу рівняння. Тут ми розглянемо методи для найбільш поширених типів рівнянь.
Усунення параметра з поліноміальних, експоненціальних та логарифмічних рівнянь
Для поліноміальних, експоненціальних або логарифмічних рівнянь, виражених у вигляді двох параметричних рівнянь, ми вибираємо рівняння, яке найбільш легко маніпулювати і вирішувати для\(t\). Підставляємо отриманий вираз for\(t\) в друге рівняння. Це дає одне рівняння в\(x\) і\(y\).
Задано\(x(t)=t^2+1\) і\(y(t)=2+t\), виключають параметр, а параметричні рівняння записують у вигляді декартового рівняння.
Рішення
Ми почнемо з рівняння для\(y\) тому, що лінійне рівняння легше вирішити для\(t\).
\[\begin{align*} y &= 2+t \\ y−2 &=t \end{align*}\]
Далі\(y−2\) замінюємо\(t\) в\(x(t)\).
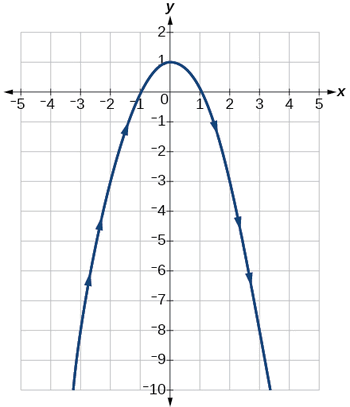
\[\begin{align*} x &= t^2+1 \\ x &= {(y−2)}^2+1 \;\;\;\;\;\;\;\; \text{Substitute the expression for }t \text{ into }x. \\ x &= y^2−4y+4+1 \\ x &= y^2−4y+5 \\ x &= y^2−4y+5 \end{align*}\]
Декартова форма є\(x=y^2−4y+5\).
Аналіз
Це рівняння для параболи, в якій в прямокутному\(x\) вираженні залежить від\(y\). З вершини кривої в\((1,2)\), графік змітається вправо. Див\(\PageIndex{7}\). Малюнок. У цьому розділі розглядаються множини рівнянь, заданих функціями\(x(t)\) і\(y(t)\), де\(t\) знаходиться незалежна змінна часу. Зверніть увагу, обидва\(x\) і\(y\) є функціями часу; так в цілому не\(y\) є функцією\(x\).
З огляду на наведені нижче рівняння, усуньте параметр і запишіть у вигляді прямокутного рівняння для\(y\) як функції\(x\).
\[\begin{align*} x(t) &= 2t^2+6 \\ y(t) &= 5−t \end{align*}\]
- Відповідь
-
\(y=5−\sqrt{\frac{1}{2}x−3}\)
Виключіть параметр і запишіть у вигляді декартового рівняння:\(x(t)=e^{−t}\) і\(y(t)=3e^t\),\(t>0\).
Рішення
Ізолювати\(e^t\).
\[\begin{align*} x &=e^{−t} \\ e^t &= \dfrac{1}{x} \end{align*}\]
Підставте вираз на\(y(t)\).
\[\begin{align*} y &= 3e^t \\ y &= 3 \left(\dfrac{1}{x}\right) \\ y &= \dfrac{3}{x} \end{align*}\]
Декартова форма є\(y=\dfrac{3}{x}\).
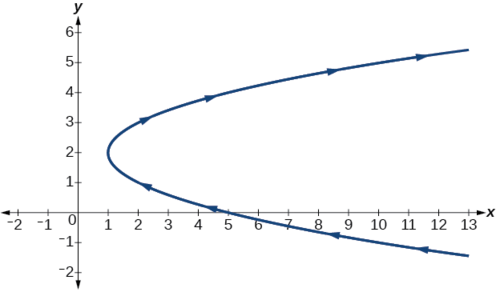
Аналіз
Графік параметричного рівняння наведено на малюнку\(\PageIndex{8a}\). Домен обмежений\(t>0\). Декартове рівняння,\(y=\dfrac{3}{x}\) показано на малюнку\(\PageIndex{8b}\) і має лише одне обмеження на область,\(x≠0\).
Виключіть параметр і запишіть у вигляді декартового рівняння:\(x(t)=\sqrt{t}+2\) і\(y(t)=\log(t)\).
Рішення
Вирішити перше рівняння для\(t\).
\[\begin{align*} x &= \sqrt{t}+2 \\ x−2 &= \sqrt{t} \\ {(x−2)}^2 &= t \;\;\;\;\;\;\;\; \text{Square both sides.} \end{align*}\]
Потім підставляємо вираз для\(t\) у\(y\) рівняння.
\[\begin{align*} y &= \log(t) \\ y &= \log{(x−2)}^2 \end{align*}\]
Декартова форма є\(y=\log{(x−2)}^2\).
Аналіз
Щоб бути впевненим, що параметричні рівняння еквівалентні декартовому рівнянню, перевірте області. Параметричні рівняння обмежують область\(x=\sqrt{t}+2\) до\(t>0\); ми обмежуємо домен\(x\) на\(x>2\). Область параметричного рівняння\(y=\log(t)\) обмежена\(t>0\); ми обмежуємо область\(y=\log{(x−2)}^2\) на\(x>2\).
Виключіть параметр і запишіть у вигляді прямокутного рівняння.
\[\begin{align*} x(t) &= t^2 \\ y(t) &= \ln t\text{, } t>0 \end{align*}\]
- Відповідь
-
\(y=\ln \sqrt{x}\)
Усунення параметра з тригонометричних рівнянь
Усунення параметра з тригонометричних рівнянь - це пряма заміна. Ми можемо використовувати декілька знайомих тригонометричних ідентичностей та теорему Піфагора.
По-перше, ми використовуємо ідентичності:
\[\begin{align*} x(t) &= a \cos t \\ y(t) &= b \sin t \end{align*}\]
Рішення для\(\cos t\) і\(\sin t\), у нас є
\[\begin{align*} \dfrac{x}{a} &= \cos t \\ \dfrac{y}{b} &= \sin t \end{align*}\]
Потім скористайтеся теоремою Піфагора:
\({\cos}^2 t+{\sin}^2 t=1\)
Заміна дає
\({\cos}^2 t+{\sin}^2 t={\left(\dfrac{x}{a}\right)}^2+{\left(\dfrac{y}{b}\right)}^2=1\)
Виключіть параметр із заданої пари тригонометричних рівнянь, де\(0≤t≤2\pi\) і накидайте графік.
\[\begin{align*} x(t) &=4 \cos t \\ y(t) &=3 \sin t \end{align*}\]
Рішення
Рішення для\(\cos t\) і\(\sin t\), у нас є
\[\begin{align*} x &=4 \cos t \\ \dfrac{x}{4} &= \cos t \\ y &=3 \sin t \\ \dfrac{y}{3} &= \sin t \end{align*}\]
Далі використовуйте піфагорійську ідентичність і зробіть заміни.
\[\begin{align*} {\cos}^2 t+{\sin}^2 t &= 1 \\ {\left(\dfrac{x}{4}\right)}^2+{\left(\dfrac{y}{3}\right)}^2 &=1 \\ \dfrac{x^2}{16}+\dfrac{y^2}{9} &=1 \end{align*}\]
Графік рівняння наведено на малюнку\(\PageIndex{9}\).
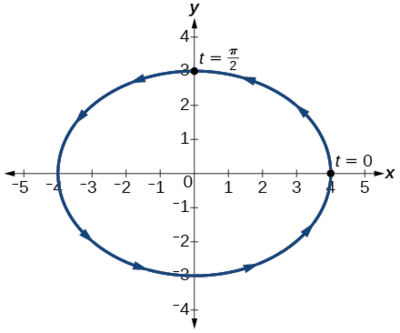
Аналіз
Застосовуючи загальні рівняння для конічних перерізів (введені в аналітичній геометрії), ми можемо ідентифікувати\(\dfrac{x^2}{16}+\dfrac{y^2}{9}=1\) як еліпс з центром\((0,0)\). Зверніть увагу,\(t=0\) що коли координати\((4,0)\), і коли\(t=\dfrac{\pi}{2}\) координати є\((0,3)\). Це показує орієнтацію кривої зі збільшенням значень\(t\).
Виключіть параметр із заданої пари параметричних рівнянь і запишіть у вигляді декартового рівняння:\(x(t)=2 \cos t\) і\(y(t)=3 \sin t\).
- Відповідь
-
\(\dfrac{x^2}{4}+\dfrac{y^2}{9}=1\)
Пошук декартових рівнянь з кривих, визначених параметрично
Коли нам дається набір параметричних рівнянь і потрібно знайти еквівалентне декартове рівняння, ми по суті «усуваємо параметр». Однак існують різні методи, які ми можемо використовувати для перезапису набору параметричних рівнянь як декартового рівняння. Найпростіший метод - встановити одне рівняння, рівне параметру, наприклад\(x(t)=t\). При цьому\(y(t)\) може бути будь-який вираз. Для прикладу розглянемо наступну пару рівнянь.
\[\begin{align*} x(t) &=t \\ y(t) &= t^2−3 \end{align*}\]
Переписування цього набору параметричних рівнянь є питанням підміни\(x\)\(t\). Таким чином, декартове рівняння є\(y=x^2−3\).
Використовуйте два різні методи, щоб знайти декартове рівняння, еквівалентне заданому набору параметричних рівнянь.
\[\begin{align*} x(t) &= 3t−2 \\ y(t) &= t+1 \end{align*}\]
Рішення
Спосіб 1. Для початку розв'яжемо\(x\) рівняння для\(t\). Тоді ми можемо підставити результат у\(y\) рівняння.
\[\begin{align*} x &= 3t−2 \\ x+2 &= 3t \\ \dfrac{x+2}{3} &= t \end{align*}\]
Тепер підставляємо вираз для\(t\) в\(y\) рівняння.
\[\begin{align*} y &= t+1 \\ y & = \left(\dfrac{x+2}{3}\right)+1 \\ y &= \dfrac{x}{3}+\dfrac{2}{3}+1 \\ y &= \dfrac{1}{3}x+\dfrac{5}{3} \end{align*}\]
Спосіб 2. Вирішити\(y\) рівняння для\(t\) і підставити цей вираз в\(x\) рівняння.
\[\begin{align*} y &= t+1 \\ y−1 &=t \end{align*}\]
Зробіть заміну, а потім вирішуйте для\(y\).
\[\begin{align*} x &= 3(y−1)−2 \\ x &= 3y−3−2 \\ x &= 3y−5 \\ x+5 &= 3y \\ \dfrac{x+5}{3} &= y \\ y &= \dfrac{1}{3}x+\dfrac{5}{3} \end{align*}\]
Задані параметричні рівняння запишіть як декартове рівняння:\(x(t)=t^3\) і\(y(t)=t^6\).
- Відповідь
-
\(y=x^2\)
Пошук параметричних рівнянь для кривих, визначених прямокутними рівняннями
Хоча ми щойно показали, що існує лише один спосіб інтерпретації набору параметричних рівнянь як прямокутного рівняння, існує кілька способів інтерпретації прямокутного рівняння як набору параметричних рівнянь. Будь-яка стратегія, яку ми можемо використовувати для пошуку параметричних рівнянь, є дійсною, якщо вона створює еквівалентність. Іншими словами, якщо ми виберемо вираз для представлення\(x\), а потім підставимо його в\(y\) рівняння, і він створює той самий графік у тій же області, що і прямокутне рівняння, то набір параметричних рівнянь є дійсним. Якщо область стає обмеженою в наборі параметричних рівнянь, а функція не допускає тих же значень для\(x\) області прямокутного рівняння, то графіки будуть іншими.
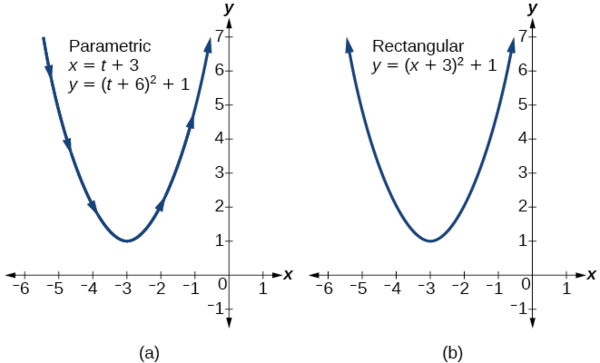
Знайти набір еквівалентних параметричних рівнянь для\(y={(x+3)}^2+1\).
Рішення
Очевидним вибором було б дозволити\(x(t)=t\). Потім\(y(t)={(t+3)}^2+1\). Але давайте спробуємо щось більш цікаве. Що робити, якщо ми дозволимо\(x=t+3\)? Тоді у нас є
\[\begin{align*} y &= {(x+3)}^2+1 \\ y &= {((t+3)+3)}^2+1 \\ y &= {(t+6)}^2+1 \end{align*}\]
Сукупність параметричних рівнянь дорівнює
\[\begin{align*} x(t) &= t+3 \\ y(t) &= {(t+6)}^2+1 \end{align*}\]
Див\(\PageIndex{10}\). Малюнок.
Отримайте доступ до цих онлайн-ресурсів для додаткової інструкції та практики з параметричними рівняннями.
- Вступ до параметричних рівнянь
- Перетворення параметричних рівнянь у прямокутну форму
Ключові концепції
- Параметризація кривої передбачає переклад прямокутного рівняння в двох змінних,\(x\) і\(y\), у два рівняння в трьох змінних\(x\),,\(y\), і\(t\). Найчастіше більше інформації отримують з безлічі параметричних рівнянь. Див. розділ Приклад\(\PageIndex{1}\)\(\PageIndex{2}\), Приклад та Приклад\(\PageIndex{3}\).
- Іноді рівняння простіше графувати при написанні в прямокутній формі. Виключаючи\(t\), рівняння в\(x\) і\(y\) є результатом.
- Для усунення\(t\) вирішуємо одне з рівнянь для\(t\), і підставляємо вираз у друге рівняння. Див. Приклад\(\PageIndex{4}\)\(\PageIndex{5}\), Приклад\(\PageIndex{6}\), Приклад та Приклад\(\PageIndex{7}\).
- Знаходження прямокутного рівняння для кривої, визначеної параметрично, в основному те саме, що і усунення параметра. \(t\)Розв'яжіть for в одному з рівнянь і підставити вираз у друге рівняння. Див\(\PageIndex{8}\). Приклад.
- Існує нескінченна кількість способів вибору набору параметричних рівнянь для кривої, визначеної як прямокутне рівняння.
- Знайдіть вираз для\(x\) такого, щоб область множини параметричних рівнянь залишилася такою ж, як і вихідне прямокутне рівняння. Див\(\PageIndex{9}\). Приклад.
