8.4: Додатки

Last updated
Save as PDF

Page ID: 58828

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

1.4 Програми
Тригонометрія часто використовується для того, що називається «непрямим вимірюванням». Це метод вимірювання недоступних відстаней за допомогою співвідношення між довжинами і кутами всередині трикутника. Два простих приклади цього процесу - вимірювання висоти високого дерева та вимірювання відстані через водойму. В обох випадках, хоча можна виміряти відстань безпосередньо, часто набагато простіше використовувати непряме вимірювання.

В одному прикладі непрямого вимірювання кут піднесення об'єкта може бути використаний для створення прямокутного трикутника, в якому відомий один кут і одна сторона. Інші сторони трикутника потім можуть бути вирішені для. У задачах у цьому тексті кут піднесення зазвичай буде вказано у задачі. Для того щоб реально виміряти кут піднесення об'єкта, можна використовувати простий транспортир.

Якщо ви хотіли виміряти висоту високого дерева, яке сидить на рівній землі, ви можете використовувати для цього спеціально модифікований транспортир. Виміряти кут піднесення допоможе модифікація транспортира шляхом прив'язки ваги до кінця струни і пров'язування іншого кінця струни через отвір в транспортирі. Як тільки транспортир буде готовий, тримайте його догори дном і приціліть верхівку дерева по прямому краю транспортира. Вага, що звисає вниз, покаже доповнення до кута піднесення. Іншими словами, якщо кут$20^{\circ},$ піднесення є, то струна розмітить вимір$70^{\circ}$ на транспортирі.

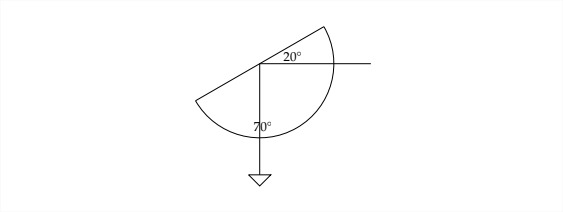
$clipboard_e13b0c9aa39c42f791e750fadf27ced45.png$

Тісно пов'язаним з поняттям кута піднесення є кут западини. Це кут, який утворюється при погляді вниз на щось зверху.

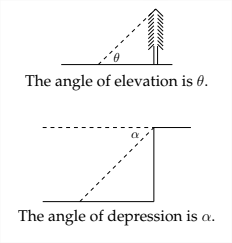
$clipboard_e06498bfd1d9482316539f4089e0412bc.png$

У ситуації, в якій вимірюється кут западини, кут піднесення і кут западини є чергуються внутрішніми кутами, що робить їх рівними.

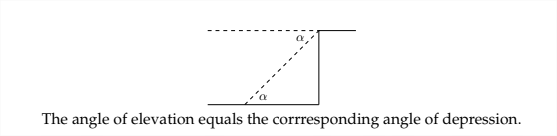
$clipboard_ea27b958c116f82e8e5ce27111e5c8a87.png$

Приклад 1$100 \mathrm{ft}$ Відступаючи по рівній землі від основи дерева, лісник вимірює кут піднесення до вершини дерева як$65^{\circ} .$ Яка висота дерева?
Ситуація, описана в задачі, створює діаграму, подібну до наведеної нижче:
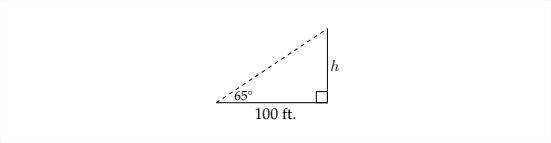
$clipboard_eef227133fd7b4c2d6401b9dc822fdce8.png$
оскільки це прямокутний трикутник, ми можемо використовувати відповідне тригонометричне співвідношення, щоб знайти висоту дерева. У цьому випадку
\ [ \ tan 65^ {\ circ} =\ frac {h} {100}
\] $100 * \tan 65^{\circ}=h$
$214.45 \approx h$
Отже, дерево має висоту близько 214,45 футів.
Приклад 2
Від вершини будівлі заввишки 125 футів кут западини перехрестя
є$34^{\circ} .$ Наскільки далеко від основи будівлі знаходиться перехрестя?
Як і в попередньому прикладі, часто корисно намалювати схему.
$clipboard_e15cc6cb037d1820dc2cd7e865eb970c7.png$

Знову ж таки, кут піднесення буде дорівнює відповідному куту западини, тому ми можемо використовувати трикутник, як показано нижче, для вирішення проблеми:
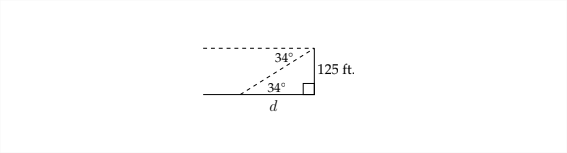
$clipboard_ee5e37044178743df9aadcfd19e7fa82f.png$
У цій задачі
\ [ \ tan 34^ {\ circ} =\ frac {125} {d}
\] Помножте з обох сторін на $d$
\ [ d *\ tan 34^ {\ circ} =125
\] Потім розділіть з обох сторін на$\tan 34^{\circ}$
\ [ \ begin {масив} {c}
\ frac {d\ tan 34^ {\ circ}} {\ tan 34^ {\ circ}} =\ frac {125} {\ tan 34^ {\ circ}}\
d\ приблизно 185.32
\ кінець {масив}
\]

Приклад 3.
Іноді проблема включає як кут піднесення, так і кут западини.

Від даху будинку 20 футів від землі кут піднесення верхньої частини багатоквартирного будинку$63^{\circ}$ і кут западини до основи будівлі є$24^{\circ} .$ Наскільки далеко від будинку знаходиться житловий будинок? Наскільки високий багатоквартирний будинок?

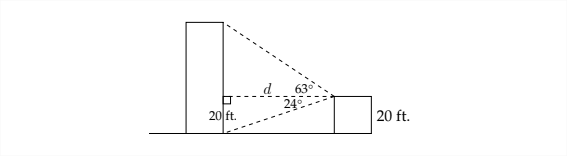
$clipboard_e6ee9f53eee59451645654fdaf6636fca.png$

Якщо спочатку працювати над нижнім трикутником, то ми знаємо, що висота трикутника є$20 \mathrm{ft}$ і кут протилежний цій стороні$24^{\circ} .$ Так, можна сказати, що:
\ [ \ begin {array} {c}
\ tan 24^ {\ circ} =\ frac {20} {d}\\
d=\ frac {20} {\ tan 24^ {\ circ}}\\
d\ приблизно 45\ mathrm {ft}
\ end {array}
\] Тепер, коли ми знаємо, що житловий будинок знаходиться на відстані 45 футів, ми можемо використовувати верхній трикутник для визначення висоти будівлі.

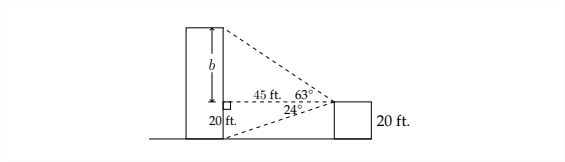
$clipboard_e3fb422c849ddcb22cdf677173370e8c5.png$

\ [ \ почати {масив} {c}
\ tan 63^ {\ circ} =\ frac {b} {45}\
45 *\ tan 63^ {\ circ} =b\
88.3\ mathrm {ft}. \ приблизно b\\
20+88.3=108.3\ mathrm {ft}
\ end {array}
\] оскільки змінна представляє$b$ лише ту частину будівлі, яка знаходиться у другому трикутнику, нам потрібно додати 20 футів,$b$ щоб знайти фактичну висоту будівлі.

Проблеми з підшипником та напрямком
Деякі застосування тригонометрії пов'язані з судноплавною навігацією. Одним із поширених методів, що використовуються для опису напрямку в цьому типі проблеми, є те, що відомо як підшипник. Підшипник описує напрямок відхиленням кута від півночі або півдня. Наприклад, напрямок, який ми зазвичай описуємо як північний схід, знаходиться рівно на півдорозі між північчю та сходом. Підшипник для північного сходу буде$N 45^{\circ} E$, і читається як «Сорок п'ять градусів на схід від півночі».

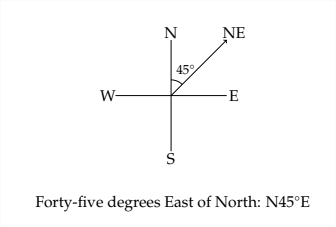
$clipboard_e64a69e0dcd5b759673704ac2da5e0ced.png$

Ось кілька прикладів того, як виглядає підшипник на діаграмі N-S-E-W.

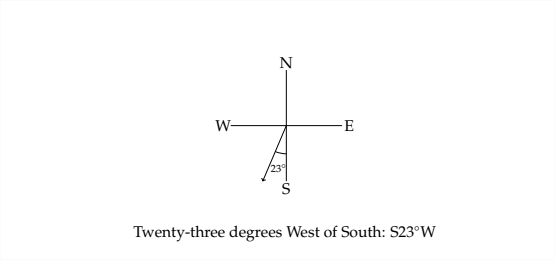
$clipboard_ee7caa1975ccdc5fb8f5a94df3023fe3b.png$

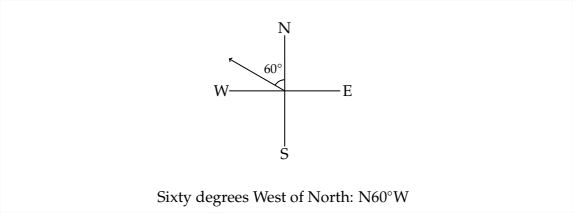
$clipboard_eba2b44a573a0337fd7d76ab16a969e6e.png$

Приклад 4
Санта-Роза, штат Каліфорнія, знаходиться в 7 милі на північ від парку Rohnert. Bodega Bay знаходиться в 19 милі на захід від парку Rohnert (як ворона летить). Що являє собою підшипник Санта Роса з Бодега Бей?
По-перше, було б корисно намалювати діаграму для представлення ситуації:

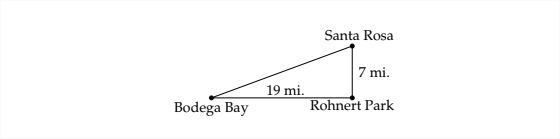
$clipboard_eeb44764ed9416885826cfb817488a521.png$

Щоб відповісти на питання нам знадобиться ще одна схема:

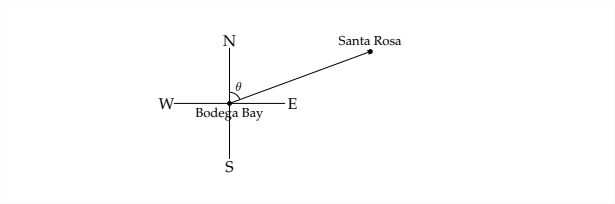
$clipboard_ec41d58665fc17d7bf1b0b32f1a0dece0.png$

Якби ми знали кут$\theta$, то можна було б зробити висновок, що підшипник Санта-Рози з затоки Бодега знаходиться в$\theta$ градусах на схід від півночі. З попередньої діаграми:
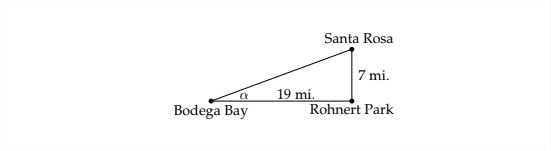
$clipboard_ebebd55c5df0dfbbc08824d491978cd6b.png$
ми бачимо, що ми не можемо знайти$\theta$ безпосередньо, але ми можемо знайти доповнення$\theta$
\ [\ tan \ alpha=\ frac {7} {19}
\]\ [ $\alpha \approx 20.2^{\circ}$
\ text {Отже,}\ theta\ приблизно 90^ {\\ circ} -20.2^ {\ circ}\ приблизно 69.8^ {\ circ}
\] Це означає, що підшипник Санта-Рози з затоки Бодега знаходиться$N 69.8^{\circ} E$, або на$69.8^{\circ}$ схід
від півночі.

Вправи 1.4
Круглі відповіді до найближчого$10^{t h}$
1. Від вершини маяка 180 футів над рівнем моря кут западини до корабля в океані є$28^{\circ} .$ Як далеко знаходиться корабель від основи маяка?
2. Вертоліт, який 700 футів у повітрі вимірює кут депресії до посадкового майданчика,$24^{\circ} .$ як далеко знаходиться посадковий майданчик від точки безпосередньо під поточне положення вертольота?
3. Дерево 88 футів кидає тінь довжиною 135 футів. Який кут піднесення сонця?
4. $\quad$Дріт 275 футів хлопець прикріплений до верхньої частини вежі зв'язку. Якщо дріт робить кут$53^{\circ}$ із землею, наскільки висока вежа?
5. Жінка, що стоїть на пагорбі, бачить будівлю, яка, як вона знає, має висоту 55 футів. Кут западини до нижньої частини будівлі дорівнює$27^{\circ}$ і кут підйому до вершини будівлі -$35^{\circ} .$ Знайти пряму відстань від жінки до будівлі.

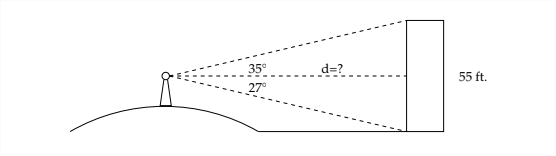
$clipboard_eab9902075f71f01de6d92facf3b98859.png$

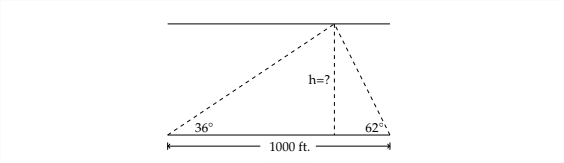
6. Щоб виміряти висоту хмарного покриву в аеропорту, прожектор світиться вгору під$62^{\circ} .$ кутом Спостерігач 1000 футів вимірює кут піднесення до прожектора, щоб бути$36^{\circ} .$ Знайдіть висоту хмарного покриву.
$clipboard_eff5f5f00f8e7d4c2803f8e250457c947.png$
7. На рівні землі водонапірна вежа знаходиться в 430 футах від основи будівлі. Від одного з верхніх поверхів будівлі кут піднесення до вершини водонапірної вежі$15^{\circ}$ і кут западини до нижньої частини водонапірної вежі є$28^{\circ} .$ Наскільки висока водонапірна вежа? Наскільки високо від землі знаходиться спостерігач?
8. Невеликий літак летить на висоті 7000 футів, слідуючи прямій дорозі прямо під ним. Автомобіль перед літаком бачиться з кутом натискання$72^{\circ}$ і автомобіль позаду літака видно з кутом натискання$48^{\circ} .$ Наскільки далеко один від одного автомобілі?
9. Від точки на підлозі кут піднесення до вершини дверного отвору становить 43". Кут піднесення до стелі безпосередньо над дверним отвором дорівнює$56^{\circ} .$ Якщо стеля на 10 футів вище підлоги, наскільки високий дверний отвір? Наскільки далеко перед дверним отвором були виміряні кути піднесення?
10. Чоловік, що стоїть на даху будівлі висотою 70 футів, дивиться на сусідню будівлю. Кут западини до даху будівлі по сусідству є$36^{\circ}$ Кут западини до нижньої частини будівлі по сусідству є$65^{\circ} .$ Наскільки висока будівля по сусідству?
11. Човен залишає гавань і проїжджає 30 миль у напрямку Човен повертається,$90^{\circ}$ а потім рухається в напрямку$S 52^{\circ} W$ 12 миль.$N 38^{\circ} W$ У той час, як далеко знаходиться човен від гавані і що несе човен від входу в гавань?

12. Людина, що йде в пустелі, подорожує 1,6 милі в напрямку$S 57^{\circ} E .$ Він потім повертає$90^{\circ}$ і продовжує ходити на 3,2 милі в напрямку У$N 33^{\circ} E .$ той час, як далеко він знаходиться від своєї відправної точки і що його несе від початкової точки?
13. Мадрас, штат Орегон, знаходиться в 26 милі на північ від Редмонда. Прайнвіль належить на схід від Редмонда і$S 34^{\circ} 42^{\prime} E$ від Мадраса. Як далеко Прайнвiлль від Редмонда?
14. Реймонд, штат Вашингтон, знаходиться в 22 милі на південь від Абердіна. Монтесано знаходиться на схід від Абердіна і$N 26^{\circ} 34^{\prime} E$ від Раймонда. Як далеко Монтесано від Раймонда?
15. Човен їздить на курсі підшипника$S 41^{\circ} 40^{\prime} W$ для 84 миль. Як далеко на південь і наскільки далеко на захід знаходиться човен від початкової точки?
16. Човен їздить на курсі підшипника$N 17^{\circ} 10^{\prime} E$ протягом 10 миль. Як далеко північ і наскільки далеко на схід знаходиться човен від своєї відправної точки?