7.2: Системи лінійних рівнянь - дві змінні
- Page ID
- 59742
- Розв'яжіть системи рівнянь шляхом побудови графіків.
- Вирішити системи рівнянь шляхом підстановки.
- Вирішити системи рівнянь шляхом додавання.
- Визначте неузгоджені системи рівнянь, що містять дві змінні.
- Висловіть розв'язок системи залежних рівнянь, що містить дві змінні.
Виробник скейтборду представляє нову лінійку дощок. Виробник відстежує його витрати, тобто суму, яку він витрачає на виробництво дощок, та його дохід, який він заробляє за рахунок продажів своїх дощок. Як компанія може визначити, чи отримує прибуток своєю новою лінією? Скільки скейтборд повинні бути вироблені і продані, перш ніж прибуток можливий? У цьому розділі ми розглянемо лінійні рівняння з двома змінними, щоб відповісти на ці та подібні питання.

Вступ до систем рівнянь
Для того, щоб дослідити такі ситуації, як виробник скейтборду, нам потрібно визнати, що ми маємо справу з більш ніж однією змінною і, ймовірно, більше одного рівняння. Система лінійних рівнянь складається з двох або більше лінійних рівнянь, що складаються з двох або більше змінних, таких, що всі рівняння в системі розглядаються одночасно. Щоб знайти унікальний розв'язок системи лінійних рівнянь, ми повинні знайти числове значення для кожної змінної в системі, яке буде задовольняти всі рівняння в системі одночасно. Деякі лінійні системи можуть не мати рішення, а інші можуть мати нескінченну кількість рішень. Для того, щоб лінійна система мала унікальне рішення, має бути принаймні стільки рівнянь, скільки змінних. Незважаючи на це, це не гарантує унікального рішення.
У цьому розділі ми розглянемо системи лінійних рівнянь в двох змінних, які складаються з двох рівнянь, що містять дві різні змінні. Для прикладу розглянемо наступну систему лінійних рівнянь у двох змінних.
\[\begin{align*} 2x+y &= 15 \\ 3x–y &= 5 \end{align*}\]
Розв'язком системи лінійних рівнянь у двох змінних є будь-яка впорядкована пара, яка задовольняє кожне рівняння незалежно. У цьому прикладі впорядкована пара\((4,7)\) є розв'язком системи лінійних рівнянь. Ми можемо перевірити рішення, підставивши значення в кожне рівняння, щоб побачити, чи задовольняє впорядкована пара обом рівнянням. Незабаром ми будемо досліджувати методи пошуку такого рішення, якщо воно існує.
\[\begin{align*} 2(4)+(7) &=15 \text{ True} \\ 3(4)−(7) &= 5 \text{ True} \end{align*}\]
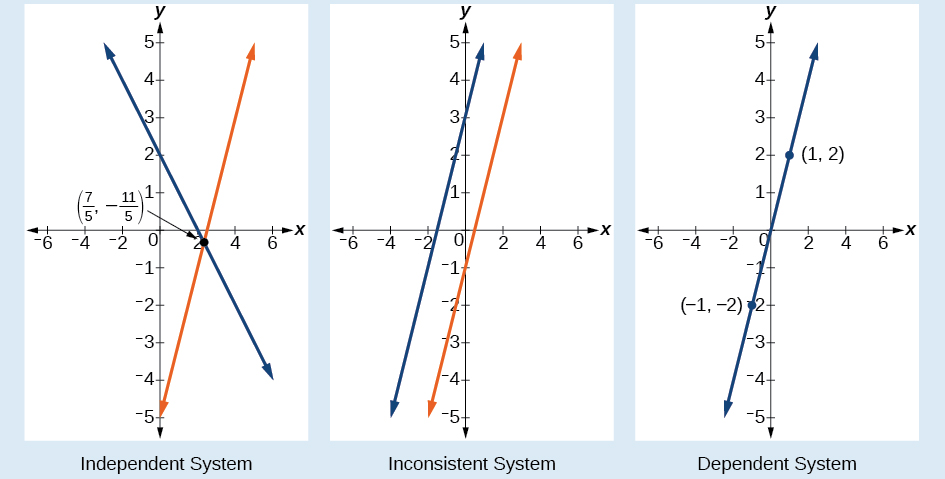
Крім розгляду кількості рівнянь і змінних, ми можемо класифікувати системи лінійних рівнянь за кількістю розв'язків. Послідовна система рівнянь має принаймні одне рішення. Послідовна система вважається незалежною системою, якщо вона має єдине рішення, наприклад приклад, який ми щойно досліджували. Дві лінії мають різний нахил і перетинаються в одній точці площини. Послідовна система вважається залежною системою, якщо рівняння мають однаковий нахил і однакові y -перехоплення. Іншими словами, лінії збігаються, тому рівняння представляють одну і ту ж лінію. Кожна точка на лінії являє собою пару координат, яка задовольняє системі. Таким чином, існує нескінченна кількість рішень.
Інший тип системи лінійних рівнянь - це непослідовна система, яка є тією, в якій рівняння представляють дві паралельні лінії. Лінії мають однаковий нахил і різні y- перехоплення. Немає точок, спільних для обох ліній; отже, немає рішення для системи.
Існує три типи систем лінійних рівнянь у двох змінних і три типи розв'язків.
- Незалежна система має рівно одну пару рішень\((x,y)\). Точка, де дві лінії перетинаються, є єдиним рішенням.
- Непослідовна система не має рішення. Зверніть увагу, що дві лінії паралельні і ніколи не перетинаються.
- Залежна система має нескінченно багато рішень. Лінії збігаються. Вони є однією лінією, тому кожна пара координат на лінії є рішенням обох рівнянь.
Рисунок\(\PageIndex{2}\) порівнює графічні зображення кожного типу системи.
- Підставте впорядковану пару в кожне рівняння в системі.
- Визначте, чи є істинні твердження результатом підстановки в обох рівняннях; якщо так, то впорядкована пара є розв'язком.
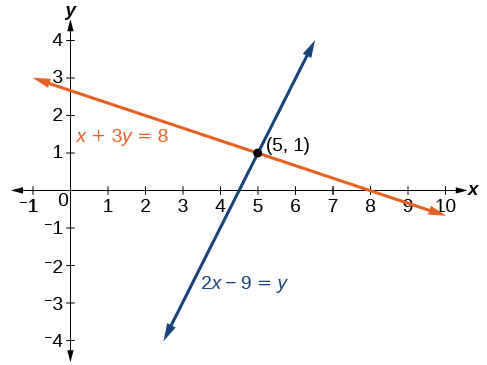
Визначте, чи\((5,1)\) є впорядкована пара розв'язком заданої системи рівнянь.
\[\begin{align*} x+3y &= 8 \\ 2x−9 &= y \end{align*}\]
Рішення
Підставити впорядковану пару\((5,1)\) в обидва рівняння.
\[ \begin{align*} (5)+3(1) &= 8 \\ 8 &= 8 \text{ True} \\ 2(5)−9 &= (1) \\ 1 &= 1 \text{ True} \end{align*}\]
Впорядкована пара\((5,1)\) задовольняє обом рівнянням, тому вона є рішенням системи.
Аналіз
Ми можемо чітко бачити рішення шляхом побудови графіка кожного рівняння. Оскільки розв'язок є впорядкованою парою, яка задовольняє обидва рівняння, це точка на обох лініях і, отже, точка перетину двох прямих. Див\(\PageIndex{3}\). Малюнок.
Визначте, чи\((8,5)\) є впорядкована пара рішенням наступної системи.
\[\begin{align*} 5x−4y &= 20 \\ 2x+1 &= 3y \end{align*}\]
- Відповідь
-
Чи не рішення.
Розв'язування систем рівнянь методом графування
Існує безліч методів розв'язання систем лінійних рівнянь. Для системи лінійних рівнянь у двох змінних ми можемо визначити як тип системи, так і рішення шляхом побудови системи рівнянь на одному наборі осей.
Розв'яжіть наступну систему рівнянь шляхом побудови графіків. Визначте тип системи.
\[\begin{align*} 2x+y &= −8 \\ x−y &= −1 \end{align*}\]
Рішення
Вирішити перше рівняння для\(y\).
\[\begin{align*} 2x+y &= −8 \\ y &= −2x−8 \end{align*}\]
Розв'яжіть друге рівняння для\(y\).
\[\begin{align*} x−y &= −1 \\ y &= x+1 \end{align*}\]
Графік обох рівнянь на тому ж наборі осей, що і на рис\(\PageIndex{4}\).
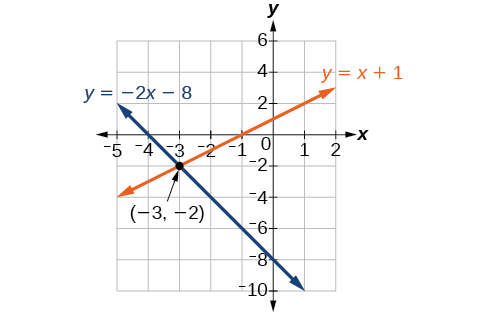
Лінії, здається, перетинаються в точці\((−3,−2)\). Ми можемо перевірити, щоб переконатися, що це рішення системи, підставивши впорядковану пару в обидва рівняння.
\[\begin{align*} 2(−3)+(−2) &= −8 \\ −8 &= −8 \text{ True} \\ (−3)−(−2) &= −1 \\ −1 &= −1 \text{ True} \end{align*}\]
Рішенням системи є впорядкована пара\((−3,−2)\), тому система незалежна.
Розв'яжіть наступну систему рівнянь шляхом побудови графіків.
\[\begin{align*} 2x−5y &= −25 \\ −4x+5y &= 35 \end{align*}\]
- Відповідь
-
Рішення системи - впорядкована пара\((−5,3)\).
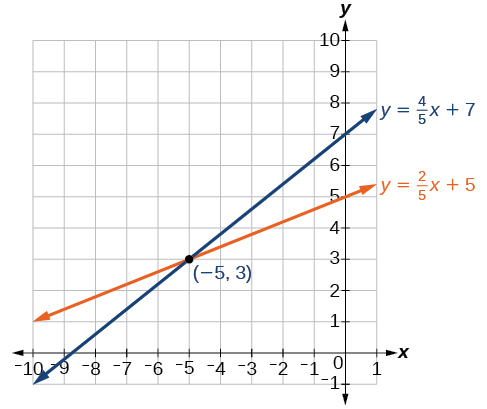
Малюнок\(\PageIndex{5}\)
Чи можна використовувати графіки, якщо система непослідовна або залежна?
Так, в обох випадках ми все ще можемо графікувати систему, щоб визначити тип системи та рішення. Якщо дві лінії паралельні, система не має рішення і є непослідовною. Якщо дві лінії ідентичні, система має нескінченні рішення і є залежною системою.
Розв'язування систем рівнянь шляхом заміщення
Розв'язування лінійної системи в двох змінних за допомогою графіків працює добре, коли рішення складається з цілих значень, але якщо наше рішення містить десяткові дроби або дроби, це не найточніший метод. Ми розглянемо ще два методи розв'язання системи лінійних рівнянь, які є більш точними, ніж графічне. Одним з таких методів є рішення системи рівнянь методом заміщення, в якому вирішуємо одне з рівнянь для однієї змінної, а потім підставляємо результат у друге рівняння для вирішення другої змінної. Нагадаємо, що ми можемо вирішити тільки для однієї змінної одночасно, саме тому метод підстановки є і цінним, і практичним.
- Розв'яжіть одне з двох рівнянь для однієї зі змінних з точки зору іншої.
- Підставляємо вираз для цієї змінної в друге рівняння, потім вирішуємо для залишилася змінної.
- Підставте це рішення в будь-яке з вихідних рівнянь, щоб знайти значення першої змінної. Якщо можливо, напишіть рішення як впорядковану пару.
- Перевірте рішення в обох рівняннях.
Вирішити наступну систему рівнянь шляхом підстановки.
\[\begin{align*} −x+y &= −5 \\ 2x−5y &= 1 \end{align*}\]
Рішення
Спочатку вирішимо перше рівняння для\(y\).
\[\begin{align*} −x+y &=−5 \\ y &= x−5 \end{align*}\]
Тепер ми можемо підставити вираз\(x−5\) для\(y\) у другому рівнянні.
\[\begin{align*} 2x−5y &= 1 \\ 2x−5(x−5) &= 1 \\ 2x−5x+25 &= 1 \\ −3x &= −24 \\ x &= 8 \end{align*}\]
Тепер підставляємо\(x=8\) в перше рівняння і вирішуємо для\(y\).
\[\begin{align*} −(8)+y &= −5 \\ y &= 3 \end{align*}\]
Наше рішення є\((8,3)\).
Перевірте рішення шляхом підстановки\((8,3)\) в обидва рівняння.
\[\begin{align*} −x+y &= −5 \\ −(8)+(3) &= −5 \text{ True} \\ 2x−5y &= 1 \\ 2(8)−5(3) &= 1 \text{ True} \end{align*}\]
Вирішити наступну систему рівнянь шляхом підстановки.
\[\begin{align*} x &= y+3 \\ 4 &= 3x−2y \end{align*}\]
- Відповідь
-
\((−2,−5)\)
Чи можна використовувати метод підстановки для розв'язання будь-якої лінійної системи у двох змінних?
Так, але метод працює найкраще, якщо одне з рівнянь містить коефіцієнт\(1\) або\(–1\) так, що нам не доведеться мати справу з дробами.
Розв'язування систем рівнянь у двох змінних методом додавання
Третім методом розв'язання систем лінійних рівнянь є метод додавання. У цьому методі ми додаємо два долі з однаковою змінною, але протилежними коефіцієнтами, щоб сума дорівнювала нулю. Звичайно, не всі системи налаштовані з двома долями однієї змінної, що мають протилежні коефіцієнти. Часто ми повинні налаштувати одне або обидва рівняння множенням так, щоб одна змінна була усунена шляхом додавання.
- Запишіть обидва рівняння з x - і y -змінними на лівій стороні знака рівності і константами праворуч.
- Напишіть одне рівняння над іншим, вибудовуючи відповідні змінні. Якщо одна зі змінних у верхньому рівнянні має протилежний коефіцієнт тієї ж змінної в нижньому рівнянні, складіть рівняння разом, виключивши одну змінну. Якщо ні, використовуйте множення на ненульове число, щоб одна зі змінних у верхньому рівнянні мала протилежний коефіцієнт тієї ж змінної в нижньому рівнянні, а потім додайте рівняння для усунення змінної.
- Вирішити отримане рівняння для залишилася змінної.
- Підставити це значення в одне з вихідних рівнянь і вирішити для другої змінної.
- Перевірте рішення, підставивши значення в інше рівняння.
Вирішити задану систему рівнянь шляхом додавання.
\[\begin{align*} x+2y &= −1 \\ −x+y &=3 \end{align*}\]
Рішення
Обидва рівняння вже встановлені рівною константі. Зверніть увагу, що коефіцієнт\(x\) у другому рівнянні\(–1\), протилежний коефіцієнту\(x\) в першому рівнянні,\(1\). Ми можемо додати два рівняння для усунення\(x\) без необхідності множення на константу.
\[\begin{align*} x+2y &= -1 \\ \underline{-x+y}& = \underline{3} \\ 3y&= 2 \\ \end{align*}\]
Тепер, коли ми усунули\(x\), ми можемо вирішити отримане рівняння для\(y\).
\[\begin{align*} 3y &= 2 \\ y &=\dfrac{2}{3} \end{align*}\]
Потім ми підставляємо це значення для\(y\) одного з вихідних рівнянь і вирішуємо для\(x\).
\[\begin{align*} −x+y &= 3 \\ −x+\dfrac{2}{3} &= 3 \\ −x &= 3−\dfrac{2}{3} \\ −x &= \dfrac{7}{3} \\ x &= −\dfrac{7}{3} \end{align*}\]
Рішення цієї системи є\(\left(−\dfrac{7}{3},\dfrac{2}{3}\right)\).
Перевірте рішення в першому рівнянні.
\[\begin{align*} x+2y &= −1 \\ \left(−\dfrac{7}{3}\right)+2\left(\dfrac{2}{3}\right) &= \\ −\dfrac{7}{3}+\dfrac{4}{3} &= −\dfrac{3}{3} \\ −1 &= −1 \;\;\;\;\;\;\;\; \text{True} \end{align*}\]
Аналіз
Ми отримуємо важливий погляд на системи рівнянь, розглядаючи графічне зображення. Див. Рисунок,\(\PageIndex{6}\) щоб знайти, що рівняння перетинаються при розв'язанні. Нам не потрібно запитувати, чи може бути друге рішення, оскільки спостереження за графіком підтверджує, що система має рівно одне рішення.
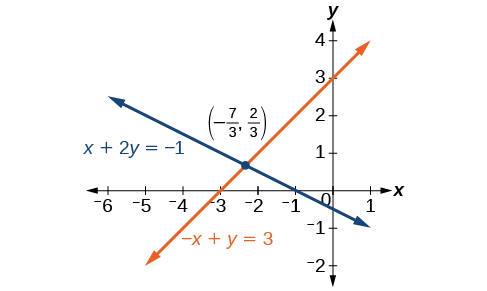
Вирішити задану систему рівнянь методом додавання.
\[\begin{align*} 3x+5y &= −11 \\ x−2y &= 11 \end{align*}\]
Рішення
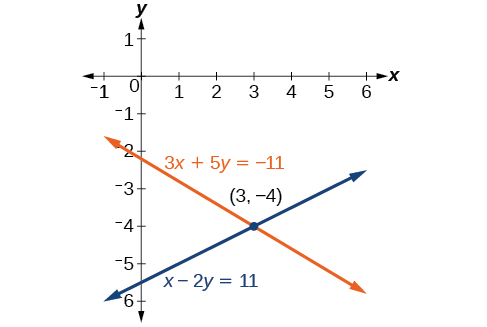
Додавання цих рівнянь, як представлено, не усуне змінну. Однак ми бачимо, що перше рівняння має\(3x\) в ньому, а друге рівняння має\(x\). Так що, якщо ми помножимо друге рівняння на\(−3\), х -членів буде додати до нуля.
\[\begin{align*} x−2y &= 11 \\ −3(x−2y) &=−3(11) \;\;\;\;\;\;\;\; \text{Multiply both sides by }−3. \\ −3x+6y &= −33 \;\;\;\;\;\;\;\;\; \text{Use the distributive property.} \end{align*}\]
Тепер давайте додамо їх.
\[\begin{align*} 3x+5y &= -11 \\ \underline{-3x+6y }& = \underline{-33} \\ 11y&= -44 \\ y&= -4 \end{align*}\]
Для останнього кроку підставляємо\(y=−4\) в одне з вихідних рівнянь і вирішуємо для\(x\).
\[\begin{align*} 3x+5y &= −11 \\ 3x+5(−4) &= −11 \\ 3x−20 &= −11 \\ 3x &= 9 \\ x &= 3 \end{align*}\]
Наше рішення - замовлена пара\((3,−4)\). Див\(\PageIndex{7}\). Малюнок. Перевірте рішення у вихідному другому рівнянні.
\[\begin{align*} x−2y &= 11 \\ (3)−2(−4) &= 3+8 \\ &= 11 \;\;\;\;\;\;\;\;\;\; \text{True} \end{align*}\]
Вирішити систему рівнянь шляхом додавання.
\[\begin{align*} 2x−7y &= 2 \\ 3x+y &= −20 \end{align*}\]
- Відповідь
-
\((−6,−2)\)
Вирішити задану систему рівнянь у двох змінних шляхом додавання.
\[\begin{align*} 2x+3y &= −16 \\ 5x−10y &= 30 \end{align*}\]
Рішення
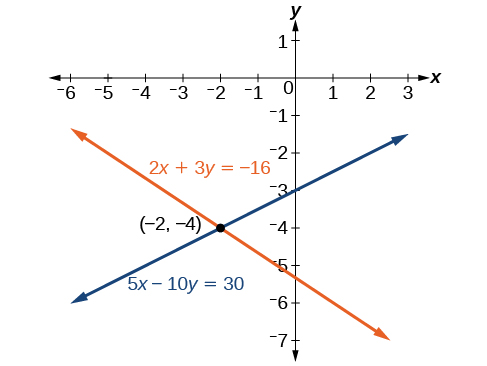
Одне рівняння має,\(2x\) а інше має\(5x\). Найменш поширене кратне,\(10x\) тому нам доведеться помножити обидва рівняння на постійну, щоб усунути одну змінну. Давайте усунемо,\(x\) множивши перше рівняння на,\(−5\) а друге рівняння на\(2\).
\[\begin{align*} −5(2x+3y) &= −5(−16) \\ −10x−15y &= 80 \\ 2(5x−10y) &= 2(30) \\ 10x−20y &= 60 \end{align*}\]
Потім ми складаємо два рівняння разом.
\[\begin{align*} -10x-15y &= 80 \\ \underline{10x-20y}& = \underline{60} \\ -35y&= 140 \\ y&= -4 \end{align*}\]
Підставити\(y=−4\) в початкове перше рівняння.
\[ \begin{align*} 2x+3(−4) &=−16 \\ 2x−12 &= −16 \\ 2x &= −4 \\ x &=−2 \end{align*}\]
Рішення є\((−2,−4)\). Перевірте це в іншому рівнянні.
\[\begin{align*} 5x−10y &= 30 \\ 5(−2)−10(−4) &= 30 \\ −10+40 &= 30 \\30 &=30 \end{align*}\]
Див\(\PageIndex{8}\). Малюнок.
Вирішити задану систему рівнянь у двох змінних шляхом додавання.
\[ \begin{align*} \dfrac{x}{3}+\dfrac{y}{6} &= 3 \\ \dfrac{x}{2}−\dfrac{y}{4} &= 1 \end{align*}\]
Рішення
Спочатку очистіть кожне рівняння дробів, множивши обидві сторони рівняння на найменш спільний знаменник.
\[\begin{align*} 6\left(\dfrac{x}{3}+\dfrac{y}{6}\right) &= 6(3) \\ 2x+y &= 18 \\ 4\left(\dfrac{x}{2}−\dfrac{y}{4}\right) &= 4(1) \\ 2x−y &= 4 \end{align*}\]
Тепер помножте друге рівняння на\(−1\) так, щоб ми могли усунути x -змінну.
\[\begin{align*} −1(2x−y) &= −1(4) \\ −2x+y &= −4 \end{align*}\]
Додайте два рівняння, щоб усунути\(x\) -змінну і вирішити отримане рівняння.
\[\begin{align*} 2x+y &= 18 \\ −2x+y &= −4 \\ 2y &= 14 \\ y &=7 \end{align*}\]
\(y=7\)Підставляємо в перше рівняння.
\[\begin{align*} 2x+(7) &= 18 \\ 2x &= 11 \\ x &= \dfrac{11}{2} \\ &= 7.5 \end{align*}\]
Рішення є\(\left(\dfrac{11}{2},7\right)\). Перевірте це в іншому рівнянні.
\[\begin{align*} \dfrac{x}{2}−\dfrac{y}{4} &= 1 \\ \dfrac{\dfrac{11}{2}}{2}−\dfrac{7}{4} &=1 \\ \dfrac{11}{4}−\dfrac{7}{4} &=1 \\ \dfrac{4}{4} &=1 \end{align*}\]
Вирішити систему рівнянь шляхом додавання.
\[\begin{align*} 2x+3y &= 8 \\ 3x+5y &= 10 \end{align*}\]
- Відповідь
-
\((10,−4)\)
Виявлення неузгоджених систем рівнянь, що містять дві змінні
Тепер, коли у нас є кілька методів розв'язання систем рівнянь, ми можемо використовувати методи для виявлення неузгоджених систем. Нагадаємо, що непослідовна система складається з паралельних ліній, які мають однаковий нахил, але різні y-перехоплення. Вони ніколи не перетинаються. При пошуку рішення неузгодженої системи ми придумаємо помилкове твердження, наприклад\(12=0\).
Вирішити наступну систему рівнянь.
\[\begin{align*} x &= 9−2y \\ x+2y &= 13 \end{align*}\]
Рішення
Ми можемо підійти до цієї проблеми двома способами. Оскільки одне рівняння вже вирішено для\(x\), найбільш очевидним кроком є використання підміни.
\[\begin{align*} x+2y &= 13 \\ (9−2y)+2y &= 13 \\ 9+0y &= 13 \\ 9 &= 13 \end{align*}\]
Зрозуміло, що це твердження є протиріччям, тому що\(9≠13\). Тому система не має рішення.
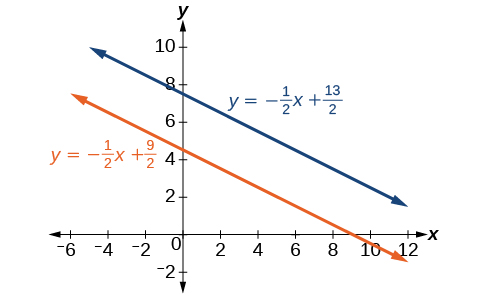
Другий підхід полягає в тому, щоб спочатку маніпулювати рівняннями так, щоб вони обидва були у формі перехоплення нахилу. Першим рівнянням маніпулюємо наступним чином.
\[\begin{align*} x &= 9−2y \\ 2y &= −x+9 \\ y &= −\dfrac{1}{2}x+\dfrac{9}{2} \end{align*}\]
Потім ми перетворюємо друге рівняння, виражене у форму перехоплення нахилу.
\[\begin{align*} x+2y &= 13 \\ 2y &= −x+13 \\ y &= −\dfrac{1}{2}x+\dfrac{13}{2} \end{align*}\]
Порівнюючи рівняння, ми бачимо, що вони мають однаковий нахил, але різні\(y\) -перехоплення. Тому лінії паралельні і не перетинаються.
\[\begin{align*} y &= −\dfrac{1}{2}x+\dfrac{9}{2} \\ y &= −\dfrac{1}{2}x+\dfrac{13}{2} \end{align*}\]
Аналіз
Запис рівнянь у формі перехоплення нахилу підтверджує, що система непослідовна, оскільки всі лінії в кінцевому підсумку перетинаються, якщо вони не паралельні. Паралельні лінії ніколи не перетинаються; таким чином, дві лінії не мають спільних точок. Графіки рівнянь в даному прикладі наведені на рис\(\PageIndex{9}\).
Розв'яжіть наступну систему рівнянь у двох змінних.
\[\begin{align*} 2y−2x &= 2 \\ 2y−2x &= 6 \end{align*}\]
- Відповідь
-
Немає рішення. Це непослідовна система.
Висловлення розв'язку системи залежних рівнянь, що містить дві змінні
Нагадаємо, що залежна система рівнянь в двох змінних - це система, в якій два рівняння представляють одну і ту ж лінію. Залежні системи мають нескінченну кількість рішень, оскільки всі точки на одній лінії також знаходяться на іншій лінії. Після використання підстановки або додавання отримане рівняння буде ідентичністю, наприклад\(0=0\).
Знайти розв'язок системи рівнянь за допомогою методу додавання.
\[\begin{align*} x+3y &= 2 \\ 3x+9y &= 6 \end{align*}\]
Рішення
За допомогою методу додавання ми хочемо усунути одну зі змінних шляхом додавання рівнянь. В даному випадку зупинимося на усуненні\(x\). Якщо помножити обидві сторони першого рівняння на\(−3\), то ми зможемо усунути змінну x.
\[\begin{align*} x+3y &= 2 \\ (−3)(x+3y) &= (−3)(2) \\ −3x−9y &= −6 \end{align*}\]
Тепер додаємо рівняння.
\[\begin{align*} -3x-9y &= -6 \\ \underline{+\space 3x+9y}& = \underline{6} \\ 0&= 0 \\ \end{align*}\]
Ми бачимо, що буде нескінченна кількість розв'язків, які задовольняють обидва рівняння.
Аналіз
Якщо ми переписали обидва рівняння у формі перехоплення нахилу, ми могли б знати, як виглядатиме рішення перед додаванням. Давайте розглянемо, що відбувається при перетворенні системи в форму ухил-перехоплення.
\[ \begin{align*} x+3y &= 2 \\ 3y &= −x+2 \\ y &= −\dfrac{1}{3}x+\dfrac{2}{3} \\ 3x+9y &= 6 \\ 9y &=−3x+6 \\ y &= −\dfrac{3}{9}x+\dfrac{6}{9} \\ y &= −\dfrac{1}{3}x+\dfrac{2}{3} \end{align*}\]
Див\(\PageIndex{10}\). Малюнок. Зверніть увагу, що результати однакові. Загальним рішенням системи є\(\left(x, −\dfrac{1}{3}x+\dfrac{2}{3}\right)\).
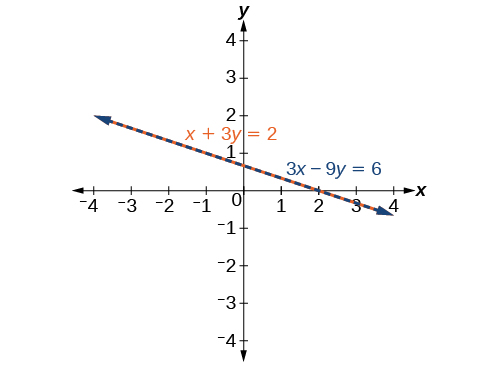
Розв'яжіть наступну систему рівнянь у двох змінних.
\[\begin{align*} y−2x &= 5 \\ −3y+6x &= −15 \end{align*}\]
- Відповідь
-
Система залежить, тому існують нескінченні рішення форми\((x,2x+5)\).
Використання систем рівнянь для дослідження прибутку
Використовуючи те, що ми дізналися про системи рівнянь, ми можемо повернутися до проблеми виготовлення скейтборду на початку розділу. Функція доходу виробника скейтборду - це функція, яка використовується для розрахунку суми грошей, яка надходить у бізнес. Він може бути представлений рівнянням\(R=xp\), де\(x\) =кількість і\(p\) =ціна. Функція доходу показана помаранчевим кольором на малюнку\(\PageIndex{11}\).
Функція витрат - це функція, яка використовується для розрахунку витрат на ведення бізнесу. Він включає постійні витрати, такі як оренда та зарплата, та змінні витрати, такі як комунальні послуги. Функція витрат показана синім кольором на рис\(\PageIndex{11}\). \(x\)Вісь -представляє кількість у сотнях одиниць. \(y\)-вісь являє собою або вартість, або дохід у сотнях доларів.
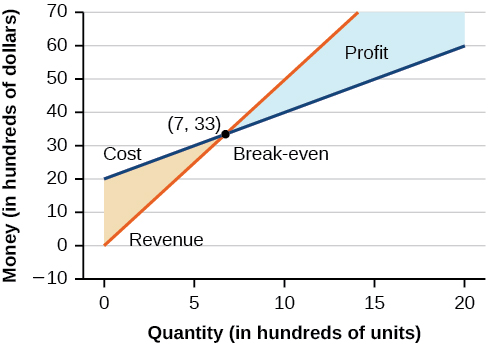
Точка, в якій дві лінії перетинаються, називається точкою беззбитковості. З графіка ми бачимо, що якщо виробляються\(700\) одиниці, вартість є\($3,300\) і дохід також\($3,300\). Іншими словами, компанія ламається, навіть якщо вони виробляють і продають\(700\) одиниці. Вони ні заробляють гроші, ні втрачають гроші.
Затінена область праворуч від точки беззбитковості представляє величини, за які компанія отримує прибуток. Затінена область зліва представляє величини, за які компанія зазнає збитків. Функція прибутку - це функція доходу мінус функція витрат, записана як\(P(x)=R(x)−C(x)\). Зрозуміло, що знання кількості, за яку вартість дорівнює доходу, має велике значення для бізнесу.
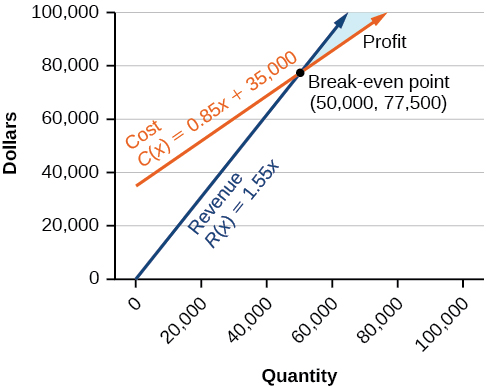
Враховуючи функцію витрат\(C(x)=0.85x+35,000\) та функцію доходу\(R(x)=1.55x\), знайдіть точку беззбитковості та функцію прибутку.
Рішення
Запишіть систему рівнянь, використовуючи\(y\) для заміни позначення функцій.
\[\begin{align*} y &= 0.85x+35,000 \\ y &= 1.55x \end{align*}\]
Підставляємо вираз\(0.85x+35,000\) з першого рівняння в друге рівняння і вирішуємо для\(x\).
\[\begin{align*} 0.85x+35,000 &= 1.55x \\ 35,000 &= 0.7x \\ 50,000 &= x \end{align*}\]
Потім ми\(x=50,000\) підставляємо або функцію витрат, або функцію доходу.
\(1.55(50,000)=77,500\)
Точка беззбитковості є\((50,000,77,500)\).
Функція прибутку знаходить за формулою\(P(x)=R(x)−C(x)\).
\[\begin{align*} P(x) &= 1.55x−(0.85x+35,000) \\ &=0.7x−35,000 \end{align*}\]
Функція прибутку є\(P(x)=0.7x−35,000\).
Аналіз
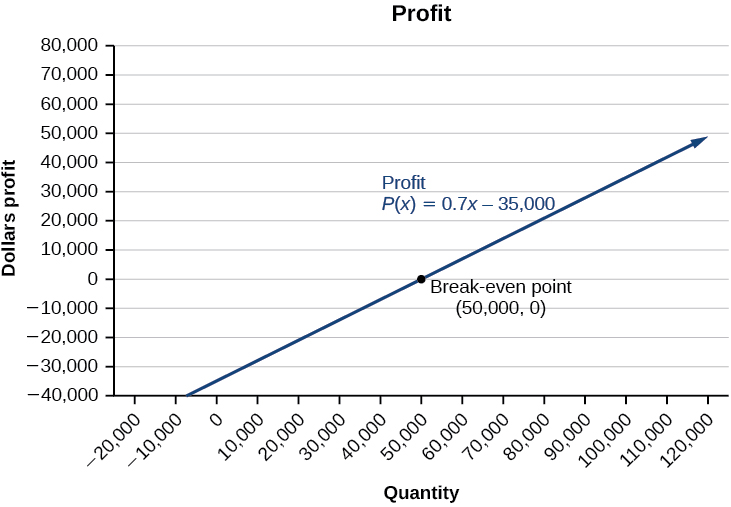
Витрати на виробництво\(50,000\) одиниць є\($77,500\), і виручка від реалізації\(50,000\) одиниць також\($77,500\). Щоб отримати прибуток, бізнес повинен виробляти і продавати більше\(50,000\) одиниць. Див\(\PageIndex{12}\). Малюнок.
Ми бачимо з графіка на малюнку\(\PageIndex{13}\), що функція прибутку має від'ємне значення до тих пір\(x=50,000\), поки графік не перетинає\(x\) вісь -. Потім графік перетворюється на позитивні\(y\) -значення і продовжує цей шлях, оскільки функція прибутку є прямою лінією. Це ілюструє, що точка беззбитковості для бізнесу виникає, коли функція прибутку є\(0\). Область зліва від точки беззбитковості представляє роботу в збиток.
Вартість квитка в цирк -\($25.00\) для дітей і\($50.00\) для дорослих. У певний день відвідуваність цирку є\(2,000\) і загальний дохід воріт становить\($70,000\). Скільки дітей і скільки дорослих купили квитки?
Рішення
Нехай\(c\) = кількість дітей і\(a\) = кількість дорослих в відвідуванні.
Загальна кількість людей - це\(2,000\). Ми можемо використовувати це, щоб написати рівняння для кількості людей у цирку того дня.
\(c+a=2,000\)
Дохід від усіх дітей можна знайти,\($25.00\) помноживши на кількість дітей,\(25c\). Дохід від усіх дорослих людей можна знайти,\($50.00\) помноживши на кількість дорослих особин,\(50a\). Загальний дохід становить\($70,000\). Ми можемо використовувати це, щоб написати рівняння доходу.
\(25c+50a=70,000\)
Тепер у нас є система лінійних рівнянь у двох змінних.
\(c+a=2,000\)
\(25c+50a=70,000\)
У першому рівнянні коефіцієнт обох змінних дорівнює\(1\). Ми можемо швидко вирішити перше рівняння для будь-якого\(c\) або\(a\). Ми вирішимо за\(a\).
\[\begin{align*} c+a &= 2,000 \\ a &= 2,000−c \end{align*}\]
Підставте вираз\(2,000−c\) у друге рівняння дляa і вирішіть для\(c\).
\[\begin{align*} 25c+50(2,000−c) &= 70,000 \\ 25c+100,000−50c &= 70,000 \\ −25c &= −30,000 \\ c &= 1,200 \end{align*}\]
Підставити\(c=1,200\) в перше рівняння, для якого потрібно вирішити\(a\).
\[\begin{align*} 1,200+a &= 2,000 \\ a &= 800 \end{align*}\]
Ми виявляємо, що\(1,200\) діти та\(800\) дорослі купували квитки в цирк того дня.
Харчування квитків в цирку обходиться\($4.00\) як для дітей, так і\($12.00\) для дорослих. Якщо квитки на\(1,650\) харчування були куплені на загальну суму\($14,200\), скільки дітей і скільки дорослих купили квитки на харчування?
- Відповідь
-
\(700\)діти,\(950\) дорослі
Отримайте доступ до цих онлайн-ресурсів для додаткових інструкцій та практики з системами лінійних рівнянь.
Ключові концепції
- Система лінійних рівнянь складається з двох або більше рівнянь, що складаються з двох або більше змінних, таких, що всі рівняння в системі розглядаються одночасно.
- Розв'язком системи лінійних рівнянь у двох змінних є будь-яка впорядкована пара, яка задовольняє кожне рівняння незалежно. Див\(\PageIndex{1}\). Приклад.
- Системи рівнянь класифікуються як незалежні з одним розв'язком, залежні з нескінченною кількістю розв'язків, або неузгоджені з відсутністю розв'язку.
- Одним із методів розв'язання системи лінійних рівнянь у двох змінних є графічне зображення. У цьому методі ми графуємо рівняння на одному і тому ж наборі осей. Див\(\PageIndex{2}\). Приклад.
- Інший метод розв'язання системи лінійних рівнянь - заміщення. У цьому методі вирішуємо для однієї змінної в одному рівнянні і підставляємо результат у друге рівняння. Див\(\PageIndex{3}\). Приклад.
- Третім методом розв'язання системи лінійних рівнянь є додавання, в якому ми можемо усунути змінну шляхом додавання протилежних коефіцієнтів відповідних змінних. Див\(\PageIndex{4}\). Приклад.
- Часто необхідно помножити одне або обидва рівняння на постійну, щоб полегшити усунення змінної при додаванні двох рівнянь разом. Див. розділ Приклад\(\PageIndex{5}\)\(\PageIndex{6}\), Приклад та Приклад\(\PageIndex{7}\).
- Будь-який метод розв'язання системи рівнянь призводить до помилкового твердження для неузгоджених систем, оскільки вони складаються з паралельних ліній, які ніколи не перетинаються. Див\(\PageIndex{8}\). Приклад.
- Рішення системи залежних рівнянь завжди буде істинним, оскільки обидва рівняння описують один і той же рядок. Див\(\PageIndex{9}\). Приклад.
- Системи рівнянь можуть бути використані для вирішення реальних проблем, які включають більше однієї змінної, наприклад, тих, що стосуються доходів, витрат і прибутку. Див. приклад\(\PageIndex{10}\) і приклад\(\PageIndex{11}\).
