4.2: Лінійні функції
- Page ID
- 59679
- Представляють лінійну функцію.
- Визначте, чи лінійна функція збільшується, зменшується або постійна.
- Інтерпретувати нахил як швидкість зміни.
- Запишіть та інтерпретуйте рівняння для лінійної функції.
- Графік лінійних функцій.
- Визначте, паралельні чи перпендикулярні лінії.
- Запишіть рівняння прямої паралельної або перпендикулярної заданій прямій.
Так само, як і у випадку з ростом рослини бамбука, існує багато ситуацій, які передбачають постійні зміни з часом. Розглянемо, наприклад, перший в світі комерційний поїзд маглев, Шанхайський поїзд MagLev (поїзд маглев), Шанхайський поїзд MagLev (рис.\(\PageIndex{1}\)). Вона з комфортом перевозить пасажирів для 30-кілометрової поїздки від аеропорту до станції метро всього за вісім хвилин.
Припустимо, що поїзд маглева повинен був проїхати велику відстань, і що поїзд підтримує постійну швидкість 83 метри в секунду протягом певного періоду часу, коли він знаходиться в 250 метрах від станції. Як ми можемо проаналізувати відстань поїзда від станції як функцію часу? У цьому розділі ми дослідимо своєрідну функцію, яка корисна для цієї мети, і використаємо її для дослідження реальних ситуацій, таких як відстань поїзда від станції в даний момент часу. Поїзд маглев повинен був подорожувати на велику відстань, і що поїзд підтримує постійну швидкість 83 метри в секунду протягом певного періоду часу один раз він знаходиться в 250 метрах від станції. Як ми можемо проаналізувати відстань поїзда від станції як функцію часу? У цьому розділі ми дослідимо своєрідну функцію, яка корисна для цієї мети, і використаємо її для дослідження реальних ситуацій, таких як відстань поїзда від станції в даний момент часу.
Представлення лінійних функцій
Функція, що описує рух поїзда, є лінійною функцією, яка визначається як функція з постійною швидкістю зміни, тобто поліном ступеня 1. Існує кілька способів представлення лінійної функції, включаючи форму слова, позначення функцій, табличну форму та графічну форму. Ми опишемо рух поїзда як функцію, використовуючи кожен метод.
Представлення лінійної функції у формі Word
Почнемо з опису лінійної функції словами. Для проблеми поїзда, яку ми щойно розглянули, наступне словоречення може бути використано для опису співвідношення функцій.
- Відстань поїзда від станції - це функція часу, протягом якого поїзд рухається з постійною швидкістю плюс його початкова відстань від станції, коли він почав рухатися з постійною швидкістю.
Швидкість - це швидкість зміни. Нагадаємо, що швидкість зміни - це міра того, наскільки швидко змінюється залежна змінна щодо незалежної змінної. Швидкість зміни для цього прикладу постійна, а це означає, що вона однакова для кожного вхідного значення. Зі збільшенням часу (введення) на 1 секунду відповідна відстань (вихід) збільшується на 83 метри. Поїзд почав рухатися з цією постійною швидкістю на відстані 250 метрів від станції.
Представлення лінійної функції в позначенні функцій
Інший підхід до представлення лінійних функцій полягає у використанні позначення функцій. Одним із прикладів позначення функції є рівняння, записане у формі, відомій як форма перехоплення нахилу прямої, де xis вхідне значення,\(m\) є швидкістю зміни і\(b\) є початковим значенням залежної змінної.
\[\begin{align*} &\text{Equation form } &y=mx+b \\[4pt] &\text{Equation notation } &f(x)=mx+b \end{align*}\]
У прикладі поїзда ми можемо використовувати позначення,\(D(t)\) в якому загальна відстань\(D\) є функцією часу\(t\). Швидкість,\(m\), становить 83 метра в секунду. Початкове значення залежної\(b\) змінної - початкова відстань від станції, 250 метрів. Ми можемо написати узагальнене рівняння для представлення руху поїзда.
\[D(t)=83t+250\]
Представлення лінійної функції в табличній формі
Третій метод представлення лінійної функції полягає у використанні таблиці. Взаємозв'язок між відстанню від станції і часом представлена на малюнку\(\PageIndex{2}\). З таблиці видно, що відстань змінюється на 83 метри за кожне збільшення часу на 1 секунду.
Ні. Вхідні дані представляють час, тому, хоча невід'ємні раціональні та ірраціональні числа можливі, негативні дійсні числа неможливі для цього прикладу. Вхідні дані складаються з невід'ємних дійсних чисел.
Представлення лінійної функції у графічному вигляді
Інший спосіб представлення лінійних функцій - візуально, використовуючи графік. Ми можемо використовувати зв'язок функції зверху\(D(t)=83t+250\), щоб намалювати графік, представлений на малюнку\(\PageIndex{3}\). Зверніть увагу, що графік є лінією. Коли ми будуємо лінійну функцію, графік завжди є лінією.
Швидкість зміни, яка є постійною, визначає ухил, або нахил лінії. Точка, в якій вхідне значення дорівнює нулю, є вертикальним перехопленням або y-перехопленням прямої. Ми бачимо з графіка на малюнку\(\PageIndex{3}\), що y-перехоплення в прикладі поїзда, який ми щойно бачили, є\((0,250)\) і представляє відстань поїзда від станції, коли він почав рухатися з постійною швидкістю.
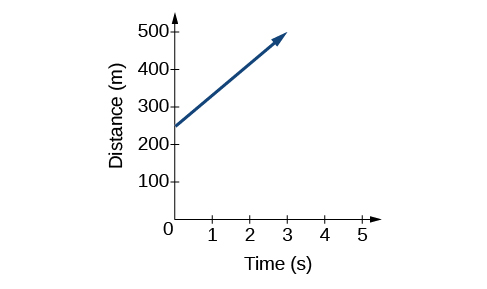
Зверніть увагу, що графік прикладу поїзда обмежений, але це не завжди так. Розглянемо графік прямої\(f(x)=2x+1\). Запитайте себе, які числа можна вводити в функцію, тобто яка область функції? Домен складається з усіх дійсних чисел, тому що будь-яке число може бути подвоєно, а потім додати його до продукту.
Лінійна функція - це функція, граф якої є лінією. Лінійні функції можуть бути записані у формі нахилу-перехоплення лінії
\[f(x)=mx+b\]
де\(b\) - початкове або початкове значення функції (при введенні,\(x=0\)), і\(m\) - постійна швидкість зміни, або нахил функції. Y-перехоплення знаходиться на\((0,b)\).
Тиск\(P\), в фунтах на квадратний дюйм (PSI) на дайвер на малюнку\(\PageIndex{4}\) залежить від її глибини нижче поверхні води\(d\), в футах. Це співвідношення може бути змодельовано рівнянням,\(P(d)=0.434d+14.696\). Повторюйте цю функцію словами.
Щоб перевстановити функцію словами, нам потрібно описати кожну частину рівняння. Тиск як функція глибини дорівнює чотириста тридцяти чотиритисячним разів глибини плюс чотирнадцять і шістсот дев'яносто шість тисячних.
Аналіз
Початкове значення, 14.696, - це тиск в PSI на дайвер на глибині 0 футів, що є поверхнею води. Швидкість зміни, або нахилу, становить 0,434 фунтів на квадратний дюйм на фут. Це говорить нам про те, що тиск на водолаза збільшується на 0,434 PSI за кожну ногу її глибина збільшується.
Визначення того, чи лінійна функція збільшується, зменшується або постійна
Лінійні функції, які ми використовували в двох попередніх прикладах, збільшувалися з часом, але не кожна лінійна функція робить. Лінійна функція може бути зростаючою, спадною або постійною. Для зростаючої функції, як у прикладі поїзда, вихідні значення збільшуються зі збільшенням вхідних значень. Графік зростаючої функції має позитивний нахил. Лінія з позитивним нахилом нахиляється вгору зліва направо, як на малюнку\(\PageIndex{5}\) (а). Для спадної функції нахил негативний. Вихідні значення зменшуються зі збільшенням вхідних значень. Лінія з негативним нахилом нахиляється вниз зліва направо, як на малюнку\(\PageIndex{5}\) (b). Якщо функція постійна, вихідні значення однакові для всіх вхідних значень, тому нахил дорівнює нулю. Лінія з ухилом нуля горизонтальна, як на малюнку\(\PageIndex{5}\) (в).
![Три графіки, що зображують зростаючу функцію, спадну функцію та постійну функцію.] Збільшення та зменшення функцій](https://math.libretexts.org/@api/deki/files/1061/CNX_Precalc_Figure_02_01_004abc.jpg)
Збільшення та зменшення функцій
Збільшення та зменшення функцій
Нахил визначає, чи є функція зростаючою лінійною функцією, спадною лінійною функцією або постійною функцією.
- \(f(x)=mx+b\)є зростаючою функцією, якщо\(m>0\).
- \(f(x)=mx+b\)є спадною функцією if\(m<0\).
- \(f(x)=mx+b\)є постійною функцією if\(m=0\).
Деякі недавні дослідження припускають, що підліток надсилає в середньому 60 текстів на день. Для кожного з наведених нижче сценаріїв знайдіть лінійну функцію, яка описує зв'язок між вхідним значенням і вихідним значенням. Потім визначте, чи є графік функції збільшенням, зменшенням або постійним.
- Загальна кількість текстів, які надсилає підліток, вважається функцією часу в днях. Вхідні дані - це кількість днів, а вивід - загальна кількість надісланих текстів.
- Підліток має ліміт 500 текстів на місяць у своєму плані даних. Вхідні дані - це кількість днів, а вивід - загальна кількість текстів, що залишилися за місяць.
- Підліток має необмежену кількість текстів у своєму тарифному плані вартістю 50 доларів на місяць. Вхідні дані - це кількість днів, а вихід - загальна вартість текстових повідомлень щомісяця.
Рішення
Проаналізуйте кожну функцію.
- Функцію можна представити як\(f(x)=60x\)\(x\) де - кількість днів. Нахил, 60, позитивний, тому функція збільшується. Це має сенс, оскільки загальна кількість текстів збільшується з кожним днем.
- Функцію можна представити як\(f(x)=500−60x\)\(x\) де - кількість днів. У цьому випадку нахил негативний, тому функція зменшується. Це має сенс, оскільки кількість текстів, що залишилися, зменшується з кожним днем, і ця функція представляє кількість текстів, що залишаються в плані даних через\(x\) дні.
- Функцію витрат можна представити як\(f(x)=50\) тому, що кількість днів не впливає на загальну вартість. Нахил дорівнює 0, тому функція постійна.
Розрахунок і інтерпретація нахилу
У прикладах, які ми бачили досі, у нас був передбачений нахил. Однак нам часто потрібно обчислити нахил заданих вхідних і вихідних значень. Задано два значення для вхідних даних\(x_2\),\(x_1\) і, і два відповідні значення для виводу,\(y_1\) і\(y_2\) —які можуть бути представлені безліччю точок,\((x_1,y_1)\) і\((x_2,y_2)\) —ми можемо обчислити нахил\(m\) наступним чином
\[\begin{align*} m &= \dfrac{\text{change in output (rise)}}{ \text{change in input (run)}} \\[4pt] &= \dfrac{{\Delta}y}{ {\Delta}x} = \dfrac{y_2−y_1}{x_2−x_1} \end{align*}\]
де\({\Delta}y\) - вертикальне зміщення і\({\Delta}x\) горизонтальне зміщення. Зверніть увагу в позначенні функції два відповідних значення для виводу\(y_1\) і\(y_2\) для функції\(f\),\(y_1=f(x_1)\) і\(y_2=f(x_2)\), так що ми могли б еквівалентно написати
\[m=\dfrac{f(x_2)-f(x_1)}{x_2-x_1} \nonumber\]
Малюнок\(\PageIndex{6}\) вказує на те, як розраховується нахил лінії між точками\((x_2,y_2)\),\((x_1,y_1)\) і,. Нагадаємо, що ухил вимірює крутизну. Чим більше абсолютне значення ухилу, тим крутіше лінія.
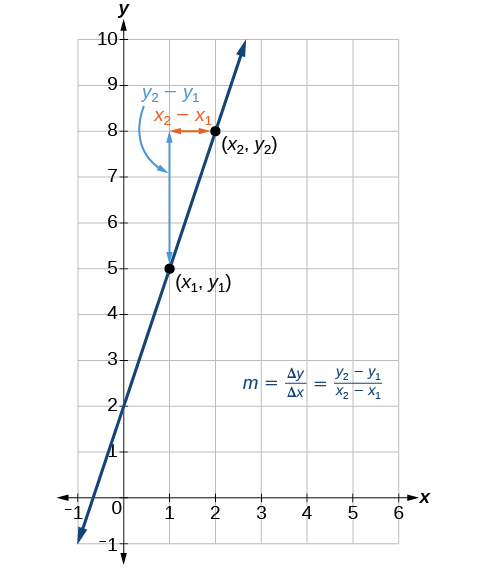
Чи завжди одиниці для нахилу\(\frac{\text{units for the output}}{ \text{units for the input}}\)?
Так. Подумайте про одиниці як про зміну вихідного значення для кожної одиниці зміни вхідного значення. Прикладом нахилу можуть бути милі на годину або долари на день. Зверніть увагу, що одиниці відображаються як співвідношення одиниць для виходу на одиниці для входу.
Нахил або швидкість зміни функції\(m\) можна обчислити відповідно до наступного:
\[m=\dfrac{\text{change in output (rise)}}{\text{change in input (run)}}=\dfrac{{\Delta}y}{{\Delta}x}=\dfrac{y_2-y_1}{x_2-x_1}\]
де\(x_1\) і\(x_2\) є вхідними значеннями,\(y_1\) і\(y_2\) є вихідними значеннями.
Задано дві точки з лінійної функції, обчислити і інтерпретувати нахил.
- Визначте одиниці для вихідних і вхідних значень.
- Обчисліть зміну вихідних значень і зміну вхідних значень.
- Інтерпретувати нахил як зміну вихідних значень на одиницю вхідного значення.
Якщо\(f(x)\) є лінійною функцією,\((3,−2)\) і\((8,1)\) є точками на лінії, знайдіть нахил. Ця функція збільшується або зменшується?
Рішення
Пари координат є\((3,−2)\) і\((8,1)\). Щоб знайти швидкість зміни, ділимо зміна виходу на зміну вхідних даних.
\[m=\dfrac{\text{change in output (rise)}}{\text{change in input (run)}}=\dfrac{1-(-2)}{8-3}=\dfrac{3}{5}\]
Ми також могли б написати нахил як\(m=0.6\). Функція збільшується тому, що\(m>0\).
Аналіз
Як зазначалося раніше, порядок, в якому ми записуємо точки, не має значення, коли ми обчислюємо нахил лінії до тих пір, поки перше вихідне значення, або y -координата, що використовується, відповідає першому вхідному значенню, або x -координата, використаному.
Якщо\(f(x)\) є лінійною функцією,\((2, 3)\) і\((0,4)\) є точками на лінії, знайдіть нахил. Ця функція збільшується або зменшується?
- Відповідь
-
\(m=\frac{4−3}{0−2} =\frac{1}{-2}=-\frac{1}{2}\); зменшується, тому що\(m<0\).
Населення міста збільшилося з 23 400 до 27 800 між 2008 і 2012 роками. Знайдіть зміну чисельності населення на рік, якщо припустити, що зміна була постійною з 2008 по 2012 рік.
Швидкість змін пов'язує зміну чисельності населення зі зміною в часі. Чисельність населення збільшилася\(27,800−23,400=4400\) людьми за чотирирічний часовий проміжок. Щоб знайти швидкість змін, поділіть зміну кількості людей на кількість років.
\[\dfrac{4,400 \text{ people}}{4 \text{ years}} =1,100 \dfrac{\text{people}}{\text{year}}\]
Так чисельність населення збільшилася на 1100 чоловік на рік.
Аналіз
Оскільки нам кажуть, що населення збільшилося, ми очікуємо, що схил буде позитивним. Тому цей позитивний нахил, який ми розрахували, є розумним.
Населення невеликого містечка збільшилася з 1442 до 1868 між 2009 і 2012 роками. Знайдіть зміну чисельності населення на рік, якщо припустити, що зміна була постійною з 2009 по 2012 рік.
- Відповідь
-
\(m=\frac{1,868−1,442}{2,012−2,009} = \frac{426}{3} =\text{ 142 people per year}\)
Написання форми точки-нахилу лінійного рівняння
До цих пір ми використовували форму перехоплення нахилу лінійного рівняння для опису лінійних функцій. Тут ми дізнаємося інший спосіб написання лінійної функції - точка-нахил форми.
\[y-y_1=m(x-x_1)\]
Форма точка-нахил походить від формули нахилу.
\[ \begin{align*} &m=\dfrac{y-y_1}{x-x_1} &\text{assuming }x{\neq}x_1 \\ &m(x-x_1)=\dfrac{y-y_1}{x-x_1}(x-x_1) &\text{Multiply both sides by }(x-x_1). \\ &m(x-x_1)=y-y_1 &\text{Simplify} \\ &y-y_1=m(x-x_1) &\text{Rearrange} \end{align*}\]
Майте на увазі, що форма перехоплення нахилу та форма точки-нахилу можуть бути використані для опису однієї і тієї ж функції. Ми можемо перейти від однієї форми до іншої, використовуючи базову алгебру. Наприклад, припустимо, нам дано рівняння у формі точки-нахилу,\(y−4=− \frac{1}{2}(x−6)\). Ми можемо перетворити його у форму перехоплення нахилу, як показано на малюнку.
\[\begin{align*} y-4&=-\dfrac{1}{2}(x-6) \\ y-4&=-\dfrac{1}{2}x+3 &\text{Distribute the }-\dfrac{1}{2}. \\ y&=-\dfrac{1}{2}x+7 &\text{Add 4 to each side.}\end{align*}\]
Тому та ж лінія може бути описана в ухилі-перехоплення вигляді як\(y=\dfrac{1}{2}x+7\).
Точково-нахильна форма лінійного рівняння набуває вигляду
\[y-y_1=m(x−x_1)\]
де\(m\) - ухил,\(x_1\) і\(y_1\) -\(y\) координати\(x\) і конкретної точки, через яку проходить лінія.
Написання рівняння прямої з використанням точки та нахилу
Форма точка-нахил особливо корисна, якщо ми знаємо одну точку та нахил лінії. Припустимо, наприклад, нам кажуть, що лінія має нахил 2 і проходить через точку\((4,1)\). Ми знаємо, що\(m=2\) і те\(x_1=4\) і\(y_1=1\). Ми можемо підставити ці значення в загальне рівняння точки-нахилу.
\[\begin{align*} y−y_1&=m(x−x_1) \\ y−1&=2(x−4) \end{align*}\]
Якщо ми хотіли потім переписати рівняння у формі перехоплення нахилу, ми застосовуємо алгебраїчні методи.
\[\begin{align*} y−1&=2(x−4) \\ y−1&=2x−8 &\text{Distribute the 2.} \\ y&=2x−7 &\text{Add 1 to each side.} \end{align*}\]
Обидва рівняння,\(y−1=2(x−4)\) і\(y=2x–7\), описують один і той же рядок. Див\(\PageIndex{7}\). Малюнок.
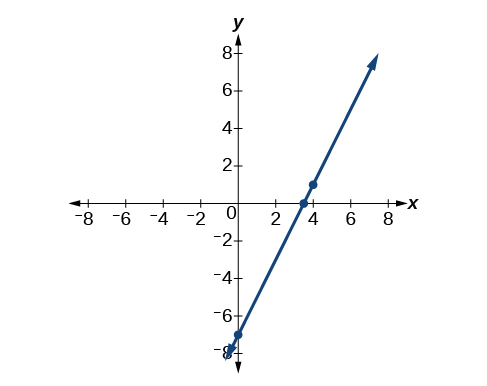
Напишіть точку-нахил форму рівняння прямої з нахилом 3, яка проходить через точку\((6,–1)\). Потім перепишіть його в ухил-перехоплення вигляді.
Рішення
Давайте розберемося, що ми знаємо з наданої інформації. Ухил дорівнює 3, так\(m=3\). Ми також знаємо один момент, тому знаємо\(x_1=6\) і\(y_1 =−1\). Тепер ми можемо підставити ці значення в загальне рівняння точки-нахилу.
\[\begin{align*} y-y_1&=m(x-x_1) \\ y−(−1)&=3(x−6) &\text{Substitute known values.} \\ y+1&=3(x−6) &\text{Distribute −1 to find point-slope form.} \end{align*}\]
Потім ми використовуємо алгебру, щоб знайти форму перехоплення нахилу.
\[\begin{align*} y+1&=3(x−6) \\ y+1&=3x−18 &\text{Distribute 3.} \\ y&=3x−19 &\text{Simplify to slope-intercept form.} \end{align*}\]
Запишіть точку-нахил форми рівняння прямої з нахилом —2, яка проходить через точку\((–2, 2)\). Потім перепишіть його в ухил-перехоплення вигляді.
- Відповідь
-
\(y−2=−2(x+2)\);\(y=−2x−2\)
Написання рівняння прямої з використанням двох точок
Точка-нахил форми рівняння також корисна, якщо ми знаємо будь-які дві точки, через які проходить лінія. Припустимо, наприклад, ми знаємо, що лінія проходить через точки\((0, 1)\) і\((3, 2)\). Ми можемо використовувати координати двох точок, щоб знайти нахил.
\[\begin{align*} m&=\dfrac{y_2-y_1}{x_2-x_1} \\ &=\dfrac{2-1}{3-0} \\ &=\dfrac{1}{3} \end{align*}\]
Тепер ми можемо використовувати знайдений нами нахил і координати однієї з точок, щоб знайти рівняння для лінії. Давайте використовувати\((0,1)\) для нашої точки зору.
\[\begin{align*} y-y_1&=m(x-x_1) \\ y-1&=\dfrac{1}{3}(x-0) \end{align*}\]
Як і раніше, ми можемо використовувати алгебру для перезапису рівняння у формі перехоплення нахилу.
\[\begin{align*} y-1&=\dfrac{1}{3}(x-0) \\ y-1&=\dfrac{1}{3}x &\text{Distribute the }\dfrac{1}{3}. \\ y&=\dfrac{1}{3}x+1 &\text{Add 1 to each side.} \end{align*}\]
Обидва рівняння описують лінію, показану на малюнку\(\PageIndex{8}\).
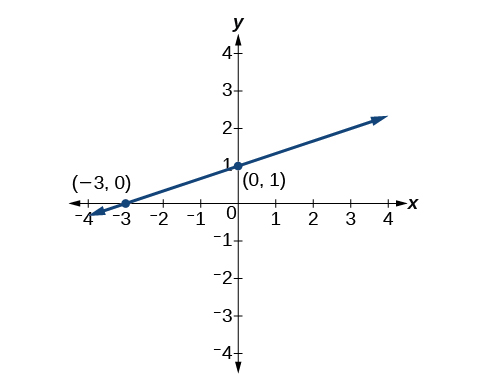
Напишіть точку-нахил форми рівняння прямої, яка проходить через точки\((5,1)\) і\((8, 7)\). Потім перепишіть його в ухил-перехоплення вигляді.
Почнемо з пошуку ухилу.
\[\begin{align*} m&=\dfrac{y_2-y_1}{x_2-x_1} \\ &=\dfrac{7-1}{8-5} \\ &=\dfrac{6}{3} \\ &= 2 \end{align*}\]
Отже\(m=2\). Далі підставляємо нахил і координати однієї з точок в загальне рівняння точка-нахил. Ми можемо вибрати будь-яку точку, але будемо використовувати\((5,1)\).
\[\begin{align*} y-y_1&=m(x-x_1) \\ y-1&=2(x-5) \end{align*}\]
Рівняння точки-нахилу прямої є\(y_2–1=2(x_2–5)\). Щоб переписати рівняння у вигляді нахилу-перехоплення, скористаємося алгеброю.
\[\begin{align*} y-1&=2(x-5) \\ y-1&=2x-10 \\ y&=2x-9 \end{align*}\]
Рівняння нахилу-перехоплення прямої є\(y=2x–9\).
\(\PageIndex{4}\): Напишіть точку-нахил форми рівняння прямої, яка проходить через точки\((–1,3)\) і\((0,0)\). Потім перепишіть його в ухил-перехоплення вигляді.
Рішення
\(y−0=−3(x−0)\);\(y=−3x\)
Написання та інтерпретація рівняння для лінійної функції
Тепер, коли ми написали рівняння для лінійних функцій як у формі нахилу, так і у формі точки-нахилу, ми можемо вибрати, який метод використовувати, виходячи з наданої нами інформації. Ця інформація може бути надана у вигляді графіка, точки і нахилу, двох точок і так далі. Подивіться на графік функції\(f\) на рис\(\PageIndex{9}\).
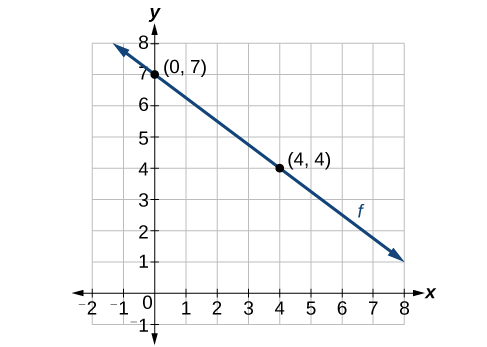
Нам не дається нахил лінії, але ми можемо вибрати будь-які дві точки на лінії, щоб знайти нахил. Давайте виберемо\((0,7)\) і\((4, 4)\). Ми можемо використовувати ці точки для розрахунку ухилу.
\[\begin{align*} m&=\dfrac{y_2-y_1}{x_2-x_1} \\ &=\dfrac{4-7}{4-0} \\&=-\dfrac{3}{4}\end{align*}\]
Тепер ми можемо підставити нахил і координати однієї з точок у форму точки-нахилу.
\[\begin{align*} y-y_1&=m(x-x_1) \\ y-4&=-\dfrac{3}{4}(x-4) \end{align*}\]
Якщо ми хочемо переписати рівняння у формі перехоплення нахилу, ми знайдемо
\[\begin{align*} y-4&=-\dfrac{3}{4}(x-4) \\ y-4 &=-\dfrac{3}{4}x+3 \\ y&=-\dfrac{3}{4}x+7\end{align*}\]
Якби ми хотіли знайти форму перехоплення нахилу без попереднього запису точки-нахилу форми, ми могли б розпізнати, що лінія перетинає вісь y, коли вихідне значення 7. Тому,\(b=7\). Тепер у нас є початкове значення\(b\) і нахил,\(m\) так що ми можемо замінити\(m\) і\(b\) в схил-перехоплення формі лінії.
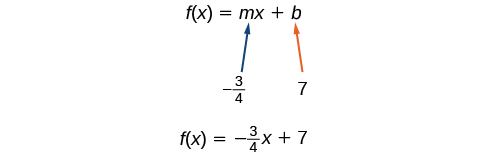
Таким чином, функція є\(f(x)=−\frac{3}{4}x+7\), і лінійне рівняння буде\(y=−\frac{3}{4}x+7\).
З огляду на графік лінійної функції, напишіть рівняння для представлення функції.
- Визначте дві точки на лінії.
- Використовуйте дві точки для розрахунку ухилу.
- Визначте, де лінія перетинає вісь y, щоб ідентифікувати перехоплення y шляхом візуального огляду.
- Підставте нахил і y-перехоплення у форму ухил-перехоплення рівняння прямої лінії.
Напишіть рівняння для лінійної функції за заданим графіком,\(f\) показаним на малюнку\(\PageIndex{11}\).
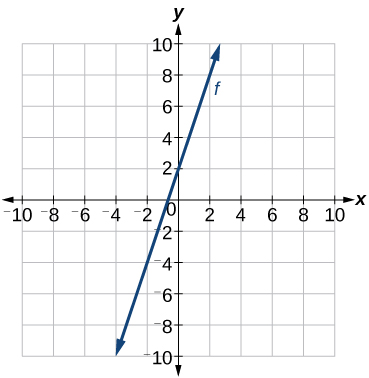
Рішення
Визначте дві точки на лінії, такі як\((0, 2)\) і\((−2,−4)\). Використовуйте точки для розрахунку ухилу.
\[\begin{align*} m&=\dfrac{y_2-y_1}{x_2-x_1} \\ &=\dfrac{4-2}{-2-0} \\ &=\dfrac{-6}{-2} \\ &=3 \end{align*}\]
Підставте нахил і координати однієї з точок у форму точки-нахилу.
\[\begin{align*} y-y_1&=m(x-x_1) \\ y-(-4)&=3(x-(-2)) \\ y+4 &= 3(x+2)\end{align*}\]
Ми можемо використовувати алгебру для перезапису рівняння у формі перехоплення нахилу.
\[\begin{align*} y+4&= 3(x+2) \\ y+4&= 3x+6 \\ y & = 3x + 2 \end{align*}\]
Аналіз
Це має сенс, тому що ми бачимо з малюнка\(\PageIndex{12}\), що лінія перетинає вісь y в точці\((0, 2)\), яка є перехопленням у, так\(b=2\).
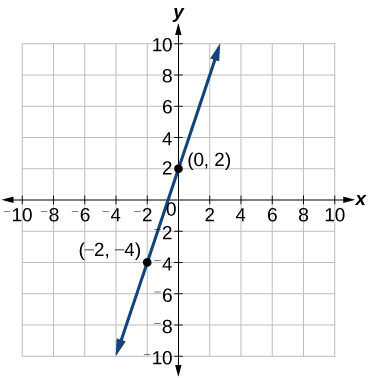
Припустимо, Бен починає компанію, в якій він несе фіксовану вартість у розмірі 1250 доларів на місяць за накладні витрати, що включає його оренду офісу. Його виробничі витрати складають $37,50 за одиницю. Напишіть лінійну функцію\(C\), де\(C(x)\) - вартість для\(x\) номенклатури, вироблених за даний місяць.
Рішення
Фіксована вартість присутня щомісяця, 1250 доларів. Витрати, які можуть варіюватися, включають вартість виробництва кожного елемента, що становить $37.50 для Бена. Змінна вартість, звана граничною вартістю, представлена 37,5. Вартість, яку несе Бен, - це сума цих двох витрат, представлених\(C(x)=1250+37.5x\).
Аналіз
Якщо Бен виробляє 100 найменувань в місяць, його щомісячна вартість представлена
\[\begin{align*} C(100)&=1250+37.5(100) \\ &=5000 \end{align*}\]
Тож його щомісячна вартість становила б 5000 доларів.
Якщо\(f\) є лінійною функцією, with\(f(3)=−2\), and\(f(8)=1\), знайти рівняння для функції у формі нахилу-перехоплення.
Рішення
Ми можемо записати задані точки, використовуючи координати.
\[\begin{align*} f(3)&= -2{\rightarrow}(3,2) \\ f(8)&=1{\rightarrow}(8,1) \end{align*}\]
Потім ми можемо використовувати точки для розрахунку нахилу.
\[\begin{align*} m&=\dfrac{y_2-y_1}{x_2-x_1} \\ &=\dfrac{1-(-2)}{8-3} \\ &=\dfrac{3}{5} \end{align*}\]
Підставте нахил і координати однієї з точок у форму точки-нахилу.
\[\begin{align*} y-y_1&=m(x-x_1) \\ y-(-2)&=\dfrac{3}{5}(x-3) \end{align*}\]
Ми можемо використовувати алгебру для перезапису рівняння у формі перехоплення нахилу.
\[\begin{align*} y+2&=\dfrac{3}{5}(x-3) \\ y+2&=\dfrac{3}{5}x-\dfrac{9}{5} \\ y&=\dfrac{3}{5}x-\dfrac{19}{5} \end{align*}\]
Якщо\(f(x)\) є лінійною функцією, with\(f(2)=–11\), and\(f(4)=−25\), знайти рівняння для функції у формі нахилу-перехоплення.
- Відповідь
-
\(y=−7x+3\)
Моделювання реальних задач з лінійними функціями
У реальному світі проблеми не завжди чітко викладені в терміні функції або представлені графіком. На щастя, ми можемо проаналізувати проблему, спочатку представивши її як лінійну функцію, а потім інтерпретувавши компоненти функції. Поки ми знаємо або можемо з'ясувати початкове значення та швидкість зміни лінійної функції, ми можемо вирішити багато різних видів реальних проблем.
Дано лінійну функцію\(f\) і початкове значення і швидкість зміни, оцінюють\(f(c)\).
- Визначте початкове значення і швидкість зміни (нахилу).
- Підставте значення на\(f(x)=mx+b\).
- Оцініть функцію за адресою\(x=c\).
Маркус в даний час має 200 пісень у своїй музичній колекції. Щомісяця він додає 15 нових пісень. Напишіть формулу для кількості пісень\(N\), в його збірці в залежності від часу\(t\), кількості місяців. Скільки пісень він буде володіти за рік?
Рішення
Початкове значення для цієї функції - 200, тому що в даний час він володіє 200 піснями\(N(0)=200\), так що це означає\(b=200\).
Кількість пісень збільшується на 15 пісень на місяць, тому швидкість зміни становить 15 пісень на місяць. Тому ми це знаємо\(m=15\). Ми можемо підставити початкове значення та швидкість зміни у форму нахилу перехоплення лінії.
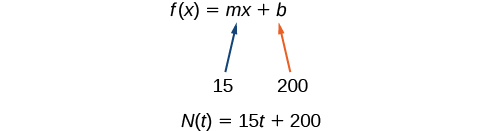
Ми можемо написати формулу\(N(t)=15t+200\).
За допомогою цієї формули ми можемо передбачити, скільки пісень у Маркуса буде за 1 рік (12 місяців). Іншими словами, ми можемо оцінити функцію за адресою\(t=12\).
\[\begin{align*} N(12)&=15(12)+200 \\ &=180+200 \\ &= 380 \end{align*}\]
Маркус матиме 380 пісень через 12 місяців.
Аналіз
Зверніть увагу, що\(N\) це зростаюча лінійна функція. Зі збільшенням вхідних даних (кількість місяців) збільшується і вихід (кількість пісень).
Працюючи продавцем страхових послуг, Ілля заробляє базову зарплату плюс комісію за кожним новим полісом. Тому тижневий дохід Іллі, я, залежить від кількості нових полісів\(n\), які він продає протягом тижня. Минулого тижня він продав 3 нових поліса, а за тиждень заробив 760 доларів. За тиждень до цього він продав 5 нових полісів і заробив 920 доларів. Знайдіть рівняння для\(I(n)\), і інтерпретуйте значення компонентів рівняння.
Рішення
Дана інформація дає нам дві пари введення-виведення:\((3,760)\) і\((5,920)\). Почнемо з пошуку швидкості змін.
\[\begin{align*} m&=\dfrac{920-760}{5-3} \\ &=\dfrac{$160}{2 \text{ policies}} \\ &=$80 \text{ per policy} \end{align*}\]
Відстеження одиниць може допомогти нам інтерпретувати цю кількість. Дохід збільшився на 160 доларів, коли кількість полісів збільшилася на 2, тому швидкість зміни становить 80 доларів за поліс. Тому Ілля заробляє комісію в розмірі 80 доларів за кожен проданий протягом тижня поліс.
Потім ми можемо вирішити для початкового значення.
\[\begin{align*} I(n)&=80n+b \\ 760&=80(3)+b \text{ when } n=3, I(3)=760 \\ 760-80(3)&=b \\ 520 & =b \end{align*}\]
Значення\(b\) є початковим значенням функції і представляє дохід Іллі\(n=0\), коли або коли нові поліси не продаються. Ми можемо трактувати це як базову зарплату Іллі за тиждень, яка не залежить від кількості проданих полісів.
Тепер ми можемо написати остаточне рівняння.
\[I(n)=80n+520 \nonumber\]
Наша остаточна інтерпретація полягає в тому, що базова зарплата Іллі становить 520 доларів на тиждень і він заробляє додаткову комісію 80 доларів за кожен проданий поліс.
рівняння для лінійної функції
Таблиця\(\PageIndex{1}\) пов'язує кількість щурів у популяції до часу, в тижнях. Використовуйте таблицю для написання лінійного рівняння.
| w, кількість тижнів | 0 | 2 | 4 | 6 |
|---|---|---|---|---|
| P (w), кількість щурів | 1000 | 1080 | 1160 | 1240 |
Рішення
З таблиці видно, що початкове значення для кількості щурів дорівнює 1000, так що\(b=1000\).
Замість того\(m\), щоб вирішувати, ми можемо сказати, дивлячись на таблицю, що населення збільшується на 80 за кожні 2 тижні, які проходять. Це означає, що швидкість зміни становить 80 щурів за 2 тижні, що можна спростити до 40 щурів на тиждень.
\[P(w)=40w+1000 \nonumber\]
Якби ми не помітили швидкість зміни з таблиці, ми все одно могли б вирішити для нахилу, використовуючи будь-які дві точки з таблиці. Наприклад, за допомогою\((2,1080)\) і\((6,1240)\)
\[\begin{align*} m&=\dfrac{1240-1080}{6-2} \\ &=\dfrac{160}{4} \\ &= 40\end{align*}\]
Чи завжди початкове значення вказано в таблиці значень, як Таблиця\(\PageIndex{1}\)?
Ні. Іноді початкове значення надається в таблиці значень, але іноді це не так. Якщо ви бачите вхід 0, то початкове значення буде відповідним виходом. Якщо початкове значення не передбачено, оскільки в таблиці немає вхідного значення, рівного 0, знайдіть нахил, підставте одну пару координат і нахил на\(f(x)=mx+b\), і вирішіть для\(b\).
\(\PageIndex{5}\): Молодому дереву було введено нову рослинну їжу, щоб перевірити його вплив на висоту дерева. Таблиця\(\PageIndex{2}\) показує висоту дерева, в футах,\(x\) місяців з моменту початку вимірювань. Напишіть лінійну функцію\(H(x)\)\(x\), де - кількість місяців з початку експерименту.
| \(x\) | 0 | 2 | 4 | 8 | 12 |
|---|---|---|---|---|---|
| \(H(x)\) | 12.5 | 13.5 | 14.5 | 16.5 | 18,5 |
Рішення
\(H(x)=0.5x+12.5\)
Ключові рівняння
- ухил-перехоплення форми лінії:\(f(x)=mx+b\)
- ухил:\(m=\dfrac{\text{change in output (rise)}}{\text{change in input (run)}}=\dfrac{{\Delta}y}{{\Delta}x}=\dfrac{y_2-y_1}{x_2-x_1}\)
- точково-похила форма лінії:\(y−y_1 =m(x-x_1)\)
Ключові концепції
- Впорядковані пари, задані лінійною функцією, представляють точки на прямій.
- Лінійні функції можуть бути представлені словами, позначеннями функцій, табличною формою та графічною формою.
- Швидкість зміни лінійної функції також відома як нахил.
- Рівняння у формі нахилу-перехоплення прямої включає нахил та початкове значення функції.
- Початкове значення, або y-перехоплення, є вихідним значенням, коли вхід лінійної функції дорівнює нулю. Це значення y точки, в якій лінія перетинає вісь y.
- Зростаюча лінійна функція призводить до графіка, який нахиляється вгору зліва направо і має позитивний нахил.
- Зниження лінійної функції призводить до графіка, який нахиляється вниз зліва направо і має негативний нахил.
- Постійна лінійна функція призводить до графіка, який є горизонтальною лінією.
- Аналіз нахилу в контексті задачі вказує, чи лінійна функція збільшується, зменшується чи постійна.
- Нахил лінійної функції можна обчислити шляхом ділення різниці між значеннями y на різницю відповідних x-значень будь-яких двох точок на прямій.
- Нахил і початкове значення можна визначити за допомогою графіка або будь-яких двох точок на лінії.
- Одним з типів позначення функції є форма ухил-перехоплення рівняння.
- Форма точка-нахил корисна для знаходження лінійного рівняння, якщо задано нахил прямої та однієї точки.
- Форма точка-нахил також зручна для знаходження лінійного рівняння при заданих двох точках, через які проходить пряма.
- Рівняння для лінійної функції можна записати, якщо\(b\) відомі нахил\(m\) і початкове значення.
- Лінійна функція може бути використана для вирішення реальних завдань.
- Лінійну функцію можна записати з табличної форми.
Виноски
1 www.chinahighlights.com/Шанг... glev-train.htm
2 www.cbsnews.com/8301-501465_1... ай-дослідження-говорить/
Глосарій
спадна лінійна функція
функція з негативним нахилом: Якщо\(f(x)=mx+b\), то\(m<0\).
збільшення лінійної функції
функція з позитивним нахилом: Якщо\(f(x)=mx+b\), то\(m>0\).
лінійна функція
функція з постійною швидкістю зміни, яка є поліномом ступеня 1, і графік якої є прямою лінією
точка-нахил форми
рівняння для рядка, що представляє лінійну функцію виду\ (y−y_1=m (x−x_1)
ухил
відношення зміни вихідних значень до зміни вхідних значень; міра крутизни рядка
ухил-перехоплення форма
рівняння для прямої, що представляє лінійну функцію у вигляді\(f(x)=mx+b\)
y-перехоплення
значення функції, коли вхідне значення дорівнює нулю; також відоме як початкове значення