2.4: Моделі та програми
- Page ID
- 59557
- Налаштуйте лінійне рівняння для вирішення реальної програми.
- Використовуйте формулу для вирішення реальної програми.
Джош сподівається отримати\(A\) в своєму класі алгебри коледжу. Він має бали\(75\),\(82\),\(95\),\(91\), і\(94\) на його перших п'яти тестах. Залишається тільки підсумковий іспит, а максимум балів, які можна заробити, є\(100\). Чи можливо Джош закінчити курс з\(A\)? Просте лінійне рівняння дасть Джошу свою відповідь.

Багато реальних додатків можуть бути змодельовані за допомогою лінійних рівнянь. Наприклад, пакет стільникового телефону може включати щомісячну плату за обслуговування плюс плату за хвилину розмови; це коштує виробнику віджетів певну суму, щоб виробляти х віджетів на місяць плюс щомісячні операційні збори; компанія з прокату автомобілів стягує щоденну плату плюс сума за милю. Це приклади додатків, з якими ми стикаємося щодня, які моделюються лінійними рівняннями. У цьому розділі ми налаштуємо і використовуємо лінійні рівняння для вирішення таких задач.
Налаштування лінійного рівняння для вирішення реальної програми
Щоб встановити або змоделювати лінійне рівняння відповідно до реального застосування, ми повинні спочатку визначити відомі величини та визначити невідому величину як змінну. Потім ми починаємо тлумачити слова як математичні вирази за допомогою математичних символів. Давайте скористаємося прикладом прокату автомобілів вище. При цьому відома вартість, наприклад\($0.10/mi\), множиться на невідому величину, кількість пройдених миль. Тому ми можемо писати\(0.10x\). Цей вираз представляє змінну вартість, оскільки вона змінюється відповідно до кількості пройдених миль.
Якщо кількість не залежить від змінної, ми зазвичай просто додаємо або віднімаємо її, відповідно до проблеми. Оскільки ці суми не змінюються, ми називаємо їх постійними витратами. Розглянемо агентство з прокату автомобілів, яке стягує\($0.10/mi\) плюс щоденну плату\($50\). Ми можемо використовувати ці величини для моделювання рівняння, яке можна використовувати для пошуку щоденної вартості оренди автомобіля\(C\).
\(C=0.10x+50 \tag{2.4.1}\)
При роботі з реальними програмами існують певні вирази, які ми можемо перевести безпосередньо в математику. У таблиці\(\PageIndex{1}\) наведено деякі поширені словесні вирази та їх еквівалентні математичні вирази.
| Вербальний | Переклад на математичні операції |
|---|---|
| Одне число перевищує інше на | \(x,x+a\) |
| Двічі більше числа | \(2x\) |
| Одне число\(a\) більше, ніж інше число | \(x,x+a\) |
| Одне число менше, ніж удвічі інше число | \(x,2x−a\) |
| Твір числа і\(a\), зменшився на\(b\) | \(ax−b\) |
| Коефіцієнт числа і числа плюс\(a\) в три рази більше числа | \(\dfrac{x}{x+a}=3x\) |
| Твір триразового числа, а число зменшилося\(b\) на\(c\) | \(3x(x−b)=c\) |
- Визначте відомі величини.
- Призначте змінну для представлення невідомої величини.
- Якщо є більше однієї невідомої кількості, знайдіть спосіб написати друге невідоме з точки зору першого.
- Напишіть рівняння, що інтерпретує слова як математичні операції.
- Вирішити рівняння. Будьте впевнені, що рішення можна пояснити словами, включаючи одиниці виміру.
Знайдіть лінійне рівняння для вирішення наступних невідомих величин: Одне число перевищує інше число на\( 17\) і їх сума дорівнює\( 31\). Знайдіть два числа.
Рішення
Нехай\( x\) дорівнює першому числу. Потім, як друге число перевищує перше на\(17\), ми можемо записати друге число як\( x +17\). Сума двох чисел дорівнює\(31\). Ми зазвичай тлумачимо слово є як знак рівності.
\[\begin{align*} x+(x+17)&= 31\\ 2x+17&= 31\\ 2x&= 14\\ x&= 7 \end{align*}\]
\[\begin{align*} x+17&= 7 + 17\\ &= 24\\ \end{align*}\]
Два числа -\(7\) і\(24\).
Знайдіть лінійне рівняння для вирішення наступних невідомих величин: Одне число - це три більше, ніж удвічі інше число. Якщо сума двох чисел дорівнює\(36\), знайдіть числа.
- Відповідь
-
\(11\)і\(25\)
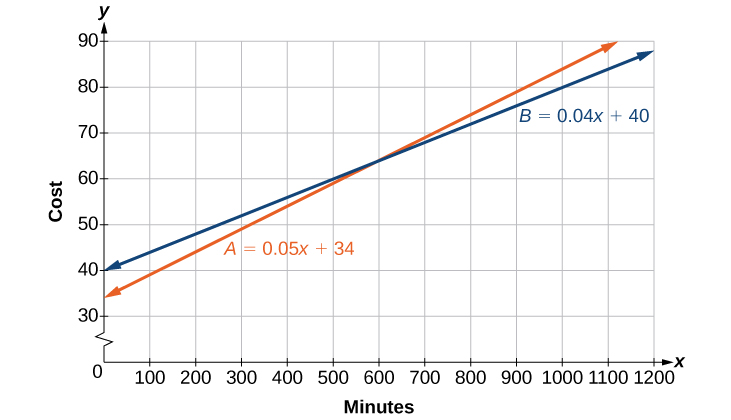
Є дві компанії стільникових телефонів, які пропонують різні пакети. Компанія А стягує щомісячну плату за обслуговування\($34\) плюс\($.05/min\) час розмови. Компанія B стягує щомісячну плату за обслуговування\($40\) плюс\($.04/min\) час розмови.
- Напишіть лінійне рівняння, яке моделює пакети, пропоновані обома компаніями.
- Якщо середня кількість хвилин, які використовуються щомісяця\(1,160\), є, яка компанія пропонує кращий план?
- Якщо середня кількість хвилин, які використовуються щомісяця\(420\), є, яка компанія пропонує кращий план?
- Скільки хвилин розмови дасть однакові щомісячні звіти від обох компаній?
Рішення
а.
Модель для компанії А може бути записана як\( A =0.05x+34\). Сюди входить змінна вартість\( 0.05x\) плюс щомісячна плата за обслуговування\($34\). Пакет компанії B стягує вищу щомісячну плату\($40\), але меншу змінну вартість\( 0.04x\). Модель компанії B може бути написана як\( B =0.04x+$40\).
б.
Якщо середня кількість хвилин, які використовуються щомісяця\(1,160\), є, ми маємо наступне:
\[\begin{align*} \text{Company A}&= 0.05(1.160)+34\\ &= 58+34\\ &= 92 \end{align*}\]
\[\begin{align*} \text{Company B}&= 0.04(1,1600)+40\\ &= 46.4+40\\ &= 86.4 \end{align*}\]
Таким чином, Компанія B пропонує нижчу\($86.40\) щомісячну вартість порівняно з\($92\) щомісячною вартістю, пропонованою компанією A, коли середня кількість хвилин, що використовуються щомісяця\(1,160\).
c.
Якщо середня кількість хвилин, які використовуються щомісяця\(420\), є, ми маємо наступне:
\[\begin{align*} \text{Company A}&= 0.05(420)+34\\ &= 21+34\\ &= 55 \end{align*}\]
\[\begin{align*} \text{Company B}&= 0.04(420)+40\\ &= 16.8+40\\ &= 56.8 \end{align*}\]
Якщо середня кількість хвилин, що використовуються щомісяця\(420\), то Компанія А пропонує нижчу щомісячну вартість\($55\) порівняно з щомісячною вартістю компанії B\($56.80\).
д.
Щоб відповісти на питання про те, скільки хвилин розмови дасть один і той же рахунок від обох компаній, слід подумати про проблему з точки зору\((x,y)\) координат: У якій точці рівні і\(x\) -значення, і\(y\) -значення? Ми можемо знайти цю точку, встановивши рівняння, рівні один одному і вирішивши для\(x\).
\[\begin{align*} 0.05x+34&= 0.04x+40\\ 0.01x&= 6\\ x&= 600 \end{align*}\]Перевірте\(x\) значення -value в кожному рівнянні.
\(0.05(600)+34=64\)
\(0.04(600)+40=64\)
Тому середньомісячна кількість\(600\) хвилин розмови робить плани рівними. Див\(\PageIndex{2}\). Малюнок.
Знайдіть лінійне рівняння для моделювання цього реального застосування: коштує компанія ABC Electronics\($2.50\) за одиницю виробляти частину, яка використовується в популярній марці настільних комп'ютерів. Компанія має щомісячні операційні витрати як\($350\) на комунальні послуги, так і\($3,300\) на зарплату. Які щомісячні витрати компанії?
- Відповідь
-
\(C=2.5x+3,650\)
Використання формули для вирішення реальної програми
Багато додатків вирішуються за допомогою відомих формул. Задача викладена, ідентифікується формула, в формулу підставляються відомі величини, рівняння вирішується для невідомого, і на питання задачі дається відповідь. Як правило, ці завдання передбачають два рівняння, що представляють дві поїздки, дві інвестиції, дві області і так далі. Приклади формул включають площу прямокутної області,
\[A=LW \tag{2.4.2}\]
периметр прямокутника,
\[P=2L+2W \tag{2.4.3}\]
і об'єм прямокутної суцільної форми,
\[V=LWH. \tag{2.4.4}\]
Коли є два невідомих, ми знаходимо спосіб написати один з точки зору іншого, тому що ми можемо вирішити тільки для однієї змінної одночасно.
\(30\; min\)Їде Андрій вранці на роботу. Він їде додому за тим же маршрутом, але це займає\(10\; min\) більше часу, і він в середньому\(10\; mi/h\) менше, ніж вранці. Як далеко Андрій їздить на роботу?
Рішення
Це проблема відстані, тому ми можемо використовувати формулу\(d =rt\), де відстань дорівнює швидкості, помноженої на час. Зверніть увагу, що коли ставка вказана в\(mi/h\), час повинен бути виражений в годинами. Послідовні одиниці вимірювання є ключовими для отримання правильного рішення.
Спочатку виявляємо відомі і невідомі величини. Ранковий заїзд Андрія на роботу бере\(30\; min\), або\(12\; h\) за курсом\(r\). Його драйв додому займає\(40\; min\), або\(23\; h\), і його швидкість в середньому\(10\; mi/h\) менше ранкової їзди. Обидві поїздки охоплюють відстань\(d\). Таблиця, наприклад Таблиця\(\PageIndex{2}\), часто корисна для відстеження інформації в таких типах проблем.
| \(d\) | \(r\) | \(t\) | |
|---|---|---|---|
| Працювати | \ (d\)» style="вирівнювання тексту: центр;» клас = "lt-математика-1632">\(d\) | \ (r\)» style="вирівнювання тексту: центр;» клас = "lt-математика-1632">\(r\) | \ (t\)» style="вирівнювання тексту: центр;» клас = "lt-math-1632">\(12\) |
| На головну | \ (d\)» style="вирівнювання тексту: центр;» клас = "lt-математика-1632">\(d\) | \ (r\)» style="вирівнювання тексту: центр;» клас = "lt-математика-1632">\(r−10\) | \ (t\)» style="вирівнювання тексту: центр;» клас = "lt-math-1632">\(23\) |
Напишіть два рівняння, по одному для кожної поїздки.
\[d=r\left(\dfrac{1}{2}\right) \qquad \text{To work} \nonumber\]
\[d=(r-10)\left(\dfrac{2}{3}\right) \qquad \text{To home} \nonumber\]
Оскільки обидва рівняння дорівнюють однаковій відстані, ставимо їх рівними один одному і вирішуємо для\(r\).
\[\begin{align*} r\left (\dfrac{1}{2} \right )&= (r-10)\left (\dfrac{2}{3} \right )\\ \dfrac{1}{2r}&= \dfrac{2}{3}r-\dfrac{20}{3}\\ \dfrac{1}{2}r-\dfrac{2}{3}r&= -\dfrac{20}{3}\\ -\dfrac{1}{6}r&= -\dfrac{20}{3}\\ r&= -\dfrac{20}{3}(-6)\\ r&= 40 \end{align*}\]
Ми вирішили для швидкості роботи,\(40\; mph\). Підставляючи\(40\) в ставку на зворотну поїздку прибутковість\(30 mi/h\). Тепер ми можемо відповісти на питання. Підставте швидкість назад в будь-яке рівняння і вирішіть для\(d\).
\[\begin{align*}d&= 40\left (\dfrac{1}{2} \right )\\ &= 20 \end{align*}\]
Відстань між домом і роботою становить\(20\; mi\).
Аналіз
Зауважте, що ми могли б очистити дроби в рівнянні, помноживши обидві сторони рівняння на РК-дисплей для вирішення\(r\).
\[\begin{align*} r\left (\dfrac{1}{2} \right)&= (r-10)\left (\dfrac{2}{3} \right )\\ 6\times r\left (\dfrac{1}{2} \right)&= 6\times (r-10)\left (\dfrac{2}{3} \right )\\ 3r&= 4(r-10)\\ 3r&= 4r-40\\ r&= 40 \end{align*}\]
У суботу вранці Дженніфер знадобилося їхати\(3.6\; h\) до будинку своєї матері на вихідні. У неділю ввечері через інтенсивний рух транспорту довелося Дженніфер\(4\; h\) повернутися додому. Її швидкість була\(5\; mi/h\) повільнішою в неділю, ніж у суботу. Якою була її швидкість в неділю?
- Відповідь
-
\(45\; mi/h\)
Периметр прямокутного відкритого дворика - це\(54\; ft\). Довжина\(3\; ft\) більше ширини. Які розміри внутрішнього дворика?
Рішення
Формула периметра стандартна:\(P=2L+2W\). У нас є дві невідомі величини, довжина і ширина. Однак ми можемо записати довжину з точки зору ширини як\(L =W+3\). У формулу підставляємо значення периметра і вираз для довжини. Часто корисно зробити ескіз і позначити сторони, як на малюнку\(\PageIndex{3}\).
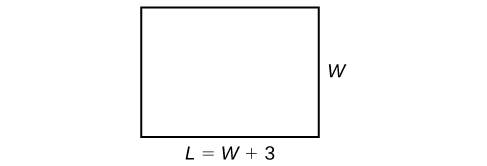
Тепер ми можемо вирішити для ширини, а потім обчислити довжину.
\[\begin{align*} P&= 2L + 2W\\ 54&= 2(W+3)+2W\\ 54&= 2W+6+2W\\ 54&= 4W+6\\ 48&= 4W\\ W&= 12 \end{align*}\]
\[\begin{align*} L&= 12+3\\ L&= 15 \end{align*}\]
Розміри становлять\(L = 15\; ft\) і\(W = 12\; ft\).
Знайдіть розміри прямокутника, враховуючи, що периметр є,\(110\; cm\) а довжина\(1\; cm\) більше ніж удвічі більше ширини.
- Відповідь
-
\(L=37\; cm\),\(W=18\; cm\)
Периметр планшета графового паперу - це\(48\space{in.}^2\). Довжина\(6\; in\). більше ширини. Знайдіть площу графічного паперу.
Рішення
Стандартна формула для площі є,\(A =LW\) однак ми вирішимо задачу за допомогою формули периметра. Причина, по якій ми використовуємо формулу периметра, полягає в тому, що ми знаємо достатньо інформації про периметр, яку формула дозволить нам вирішити для одного з невідомих. Оскільки як периметр, так і площа використовують довжину і ширину як розміри, вони часто використовуються разом для вирішення такої проблеми, як ця.
Ми знаємо, що довжина\(6\; in\). більше, ніж ширина, так що ми можемо написати довжину як\(L =W+6\). Підставте значення периметра і вираз для довжини в формулу периметра і знайдіть довжину.
\[\begin{align*} P&= 2L + 2W\\ 48&= 2(W+6)+2W\\ 48&= 2W+12+2W\\ 48&= 4W+12\\ 36&= 4W\\ W&= 9 \end{align*}\]
\[\begin{align*}L&= 9+6\\ L&= 15 \end{align*}\]
Тепер знаходимо площу, задану розмірами\(L = 15\; in\). і\(W = 9\; in\).
\[\begin{align*} A&= LW\\ A&=15(9)\\ A&= 135\space{in.}^2 \end{align*}\]
Площа є\(135\space{in.}^2\).
Ігрова кімната має периметр\(70\; ft\). Довжина на п'ять більше, ніж в два рази більше ширини. Скільки\(ft^2\) нового килимового покриття слід замовити?
- Відповідь
-
\(250\space{ft}^2\)
Знайдіть розміри транспортної коробки, враховуючи, що довжина вдвічі більше ширини, висота -\(8\; \) в, а обсяг -\(1,600\space{in.}^3\).
Рішення
Формула для обсягу коробки наведена як\(V =LWH\), добуток довжини, ширини і висоти. Нам дано\(L =2W\), що, і\(H =8\). Обсяг є\(1,600\; \text{cubic inches}\).
\[\begin{align*} V&= LWH\\ 1600&= (2W)W(8)\\ 1600&= 16W^2\\ 100&= W^2\\ 10&= W \end{align*}\]Розміри\(L = 20\; in\) становлять,\(W= 10\; in\), і\(H = 8\; in\).
Аналіз
Зауважте, що квадратний корінь\(W^2\) призведе до позитивного та від'ємного значення. Однак, оскільки ми описуємо ширину, ми можемо використовувати тільки позитивний результат.
Отримайте доступ до цих онлайн-ресурсів для додаткових інструкцій та практики з моделями та додатками лінійних рівнянь.
- Розв'язування задач за допомогою лінійних рівнянь
- Розв'язування задач за допомогою рівнянь
- Знаходження розмірів площі з урахуванням периметра
- Знайти відстань між містами за формулою distance = rate* time
- Застосування лінійного рівняння (Написати рівняння вартості)
Ключові поняття
- Лінійне рівняння може бути використано для розв'язання невідомої в числовій задачі. Див. Приклад.
- Додатки можуть бути записані як математичні задачі, визначаючи відомі величини та привласнюючи змінну невідомим величинам. Див. Приклад.
- Існує багато відомих формул, які можна використовувати для вирішення додатків. Задачі на відстань, наприклад, вирішуються за допомогою\(d = rt\) формули. Див. Приклад.
- Багато задач геометрії вирішуються за допомогою формули периметра\(P =2L+2W\)\(A =LW\), формули площі або формули об'єму\(V =LWH\). Див. розділ Приклад , Приклад та Приклад.
