6.2: Піфагорійська ідентичність

Теорема Піфагора працює над прямими трикутниками. Якщо ви вважаєте$x$ координату точки уздовж одиничного кола косинусом, а$y$ координату точки - синусом, а відстань до початку - 1, то теорема Піфагора негайно дає ідентичність:

\ (
\ begin {масив} {l}
y^ {2} +x^ {2} =1\
\ sin ^ {2} x+\ cos ^ {2} x = 1
\ end {масив}
\)

Спостережливий студент може здогадатися, що інші ідентичності Піфагора існують з рештою тригонометричних функцій. Чи є$\tan ^{2} x+\cot ^{2} x=1$ законною особистістю?

Піфагора ідентичності

Доказом ідентичності Піфагора для синуса і косинуса є, по суті, просто малювання прямокутного трикутника в одиничному колі, ідентифікуючи косинус як$x$ координату, синус як$y$ координату і 1 як гіпотенузу.

$\cos ^{2} x+\sin ^{2} x=1$

або

$\sin ^{2} x+\cos ^{2} x=1$

Дві інші ідентичності Піфагора:

• $1+\cot ^{2} x=\csc ^{2} x$
• $\tan ^{2} x+1=\sec ^{2} x$

Щоб вивести ці дві ідентичності Піфагора, розділіть початкову піфагорійську ідентичність на$\sin ^{2} x$ і$\cos ^{2} x$ відповідно.

Щоб вивести піфагорійську ідентичність,$1+\cot ^{2} x=\csc ^{2} x$ розділіть на$\sin ^{2} x$ і спростіть.

$\begin{aligned} \frac{\sin ^{2} x}{\sin ^{2} x}+\frac{\cos ^{2} x}{\sin ^{2} x} &=\frac{1}{\sin ^{2} x} \\ 1+\cot ^{2} x &=\csc ^{2} x \end{aligned}$

Аналогічно, щоб вивести піфагорійську ідентичність$\tan ^{2} x+1=\sec ^{2} x$, розділіть на$\cos ^{2} x$ і спростіть.

\ почати {вирівняний}
\ розрив {\ sin ^ {2} x} {\ cos ^ {2} x} +\ frac {\ cos ^ {2} x} {\ cos ^ {2} x} &=\ frac {1} {\ cos ^ {2} x}\
\ tan ^ {2} x+1 &=\ сек ^ {2} х
\ кінець {вирівняний}

Приклади

Приклад 1

Раніше вас запитали, чи$\tan ^{2} x+\cot ^{2} x=1$ є законною особистістю. Кофункції не завжди пов'язані безпосередньо через піфагорійську ідентичність.

$\tan ^{2} x+\cot ^{2} x \neq 1$

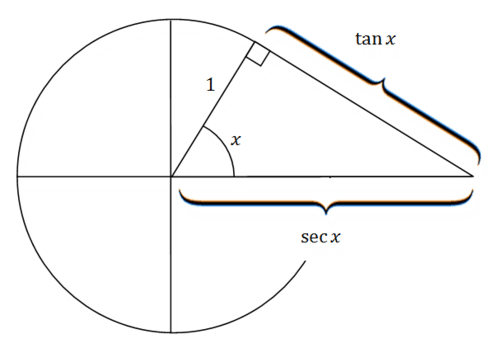
Візуально прямокутний трикутник, що з'єднує дотичну і січну, також можна спостерігати в одиничному колі. Більшість людей не знають, що тангенс називається «дотичною», оскільки він відноситься до відстані дотичної лінії від точки на одиничному колі до$x$ осі. Подивіться на картинку нижче і подумайте, чому має сенс, що$\tan x$ і$\sec x$ так позначено. $\tan x=\frac{o p p}{a d j} .$так як прилегла сторона дорівнює 1 (радіус кола), тан$x$ просто дорівнює протилежній стороні. Подібну логіку можна пояснити і розміщення$\sec x$.

Приклад 2

Спростіть наступний вираз:$\frac{\sin x(\csc x-\sin x)}{1-\sin x}$

\ (
\ почати {вирівняний}
\ розрив {\ sin x (\ csc x-\ sin x)} {1-\ sin x} &=\ frac {\ sin x\ cdot\ cdot\ csc x-\ sin ^ {2} x} {1-\ sin x} {1-\ sin x}\\
&=\\ гідророзриву {(1-\ sin x) (1+\ sin x)} {1-\ sin x}\\
&= 1+\ гріх х
\ кінець {
вирівняні}
\)

Зверніть увагу, що факторинг піфагорійської ідентичності є одним з найпотужніших і поширених додатків.

Приклад 3

Доведіть наступну тригонометричну ідентичність. $\left(\sec ^{2} x+\csc ^{2} x\right)-\left(\tan ^{2} x+\cot ^{2} x\right)=2$

Групуйте терміни та застосуйте іншу форму двох двох піфагорієвих ідентичностей, які є$1+\cot ^{2} x=\csc ^{2} x$ і$\tan ^{2} x+1=\sec ^{2} x$

\ (
\ почати {вирівняний}
\ лівий (\ сек ^ {2} x+\ csc ^ {2} х\ праворуч) -\ ліворуч (\ тан ^ {2} x+\ дитяче ^ {2} х\ праворуч) &=\ сек ^ {2} x-\ tan ^ {2} x+\ csc ^ {2} x-\
cot ^ {2} x\\
= 2
\ кінець {вирівняний}
\)

Приклад 4

Спростіть наступний вираз. Примітка:$\sec ^{2} x=\frac{1}{\cos ^{2} x}$

\ (
\ почати {вирівняний}
\ лівий (\ сек ^ {2} х\ вправо)\ лівий (1-\ sin ^ {2} х\ праворуч) -&\ лівий (\ frac {\ sin x} {\ csc x} +\ frac {\ cos x} {\ сек x}\ праворуч)\\
(&\ ліворуч. \ сек ^ {2} х\ вправо)\ ліворуч (1-\ sin ^ {2} х\ праворуч) -\ лівий (\ frac {\ sin x} {\ csc x} +\ cos x} {\ сек x}\ праворуч)\\
&=\ сек ^ {2} x\ cdot\ cos ^ {2} х-\ ліворуч (\ sin ^ {2} x+ cos ^ {2} х\ праворуч)\\
&=1-1\
&=0
\ кінець {вирівняний}
\)

Приклад 5

Спростіть наступний вираз.

\ (
(\ cos t-\ sin t) ^ {2} + (\ cos t+\ sin t) ^ {2}
\)

Зверніть увагу, що спочатку вираз не збігається з піфагорійською ідентичністю.

\ (
\ почати {масив} {l}
(\ cos t-\ sin t) ^ {2} + (\ cos t+\ sin t) ^ {2}\
=\ cos ^ {2}
t-2\ cos ^ {2} t+2\ cos t\ sin t\ sin ^ {2} t+2\ cos t\ sin ^ {2} t\\ sin ^ {2} t\ cos t\ sin ^ {2} t+1+2\ cos t\ sin t\\
=2
\ end {масив}
\)

Рецензія

Доведіть кожне з наступних дій:

1. $\left(1-\cos ^{2} x\right)\left(1+\cot ^{2} x\right)=1$

2. $\cos x\left(1-\sin ^{2} x\right)=\cos ^{3} x$

3. $\sin ^{2} x=(1-\cos x)(1+\cos x)$

4. $\sin x=\frac{\sin ^{2} x+\cos ^{2} x}{\csc x}$

5. $\sin ^{4} x-\cos ^{4} x=\sin ^{2} x-\cos ^{2} x$

6. $\sin ^{2} x \cos ^{3} x=\left(\sin ^{2} x-\sin ^{4} x\right)(\cos x)$

Максимально спрощуйте кожен вираз.

7. $\tan ^{3} x \csc ^{3} x$

8. $\frac{\csc ^{2} x-1}{\sec ^{2} x}$

9. $\frac{1-\sin ^{2} x}{1+\sin x}$

10. $\sqrt{1-\cos ^{2} x}$

11. $\frac{\sin ^{2} x-\sin ^{4} x}{\cos ^{2} x}$

12. $\left(1+\tan ^{2} x\right)\left(\sec ^{2} x\right)$

13. $\frac{\sin ^{2} x+\tan ^{2} x+\cos ^{2} x}{\sec x}$

14. $\frac{1+\tan ^{2} x}{\csc ^{2} x}$

15. $\frac{1-\sin ^{2} x}{\cos x}$

...