1.20: Класифікація багатокутників у координатній площині
- Page ID
- 54971

Паркер бере свій перший клас малювання, хоча вона не має великих надій. Коли вона входить до класу в перший день, її вчитель мистецтва підтягує картину міського пейзажу і каже їм, що всі вони зможуть намалювати це до кінця тижня. Її вчитель дає їм кожну копію цієї картини і каже їм, що їх перше завдання - розбити картину на її основні форми. Паркер абсолютно розгублений і переповнений. Як Паркер може зрозуміти, як розбити картинку на форми?
У цій концепції ви дізнаєтеся, як графувати геометричні фігури, задані координати вершин і ідентифікувати графічні фігури.
Класифікація багатокутників у координатній площині
Координатна сітка - це сітка, в якій розміщуються точки. Зазвичай він має дві або більше пересічних ліній, які ділять площину на квадранти, і в яких визначені впорядковані пари або координати. Зазвичай він має чотири квадранти, або секції, до нього.
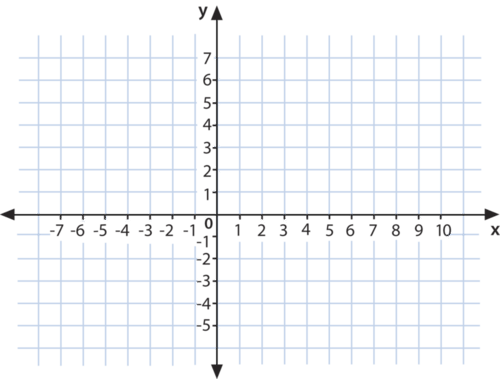 Малюнок\(\PageIndex{2}\)
Малюнок\(\PageIndex{2}\)Походження - це місце, де дві лінії перетинаються. Його координати визначаються як\((0,0)\).
\(x\)-вісь - це лінія, що йде зліва направо, яка має визначені на ній цифри і зазвичай позначена символом "\(x\)». Знайдено\(x\) -координату впорядкованої пари по відношенню до неї. Всі точки, розташовані на\(x\) -осі, мають\(y\) -координату 0.
\(y\)-вісь - це центральна лінія, яка проходить вгору-вниз і позначена символом "\(y\)». Y-координати будуються по відношенню до цієї осі. Знову ж таки, всі\(x\) -координати точок, розташованих на\(y\) -осі, дорівнюють 0.
Впорядкована пара - це список з двох чисел у дужках, розділених комою так:\((5,-3)\). Він повідомляє, де точка знаходиться на координатній площині. Перше число\(x\) - координата. Він говорить вам, куди йти на\(x\) -осі. Якщо він позитивний, ви йдете вправо. Якщо він негативний, ви йдете вліво. Друге число - y-координата. Він говорить вам, куди йти на\(y\) -осі. Якщо це позитивно, ви піднімаєтеся вгору. Якщо він негативний, ви йдете вниз.
Вершина фігури - це місце, де дві сторони фігури об'єднуються. Загалом, коли форма визначається всередині координатної площини, вона визначається вершинами, а потім лінії малюються для їх з'єднання.
Багатокутник - це будь-яка форма, що складається з прямолінійних або прямих ліній. Найменший багатокутник - це трикутник, який має три сторони. П'ятигранна фігура - п'ятикутник. І багато багатокутників з більшою кількістю сторін, ніж п'ять, також названі.
Прямий кут - це кут, який виглядає так, як зустрічаються осі на координатній площині.
Паралельні лінії - це лінії, які будуть тривати вічно, але ніколи не зійдуться.
До категорії чотиригранних багатокутників відносяться:
- квадрат, який має чотири сторони однакової довжини і його кути всі прямі кути;
- ромб, який, як і квадрат, має чотири рівні сторони, але є «нахиленим»;
- прямокутник, який має дві пари сторін, які рівні, і всі його кути є прямими кутами;
- трапеція, яка може не мати рівних сторін, але має дві паралельні лінії; і
- паралелограм, який має два набори паралельних ліній, які рівні по довжині один одному (але, як і ромб, це «tilty»).
Для того, щоб намалювати фігуру в координатній площині, ви просто графуєте кожну з вершин, а потім з'єднайте їх прямими лініями так, щоб жодна з ліній не перетиналася. Кількість сторін у вас така ж, як і кількість вершин. Так трикутник, наприклад, визначається з трьома вершинами.
Ось приклад.
Графік фігури з координатами\(A(−4, 3) B(2, 3) C(2,−1) D(−4,−1)\). Закінчивши, назвіть фігуру, яка була намальована на сітці.
Спочатку нанесіть кожну точку на координатній сітці, а потім з'єднайте лінії.
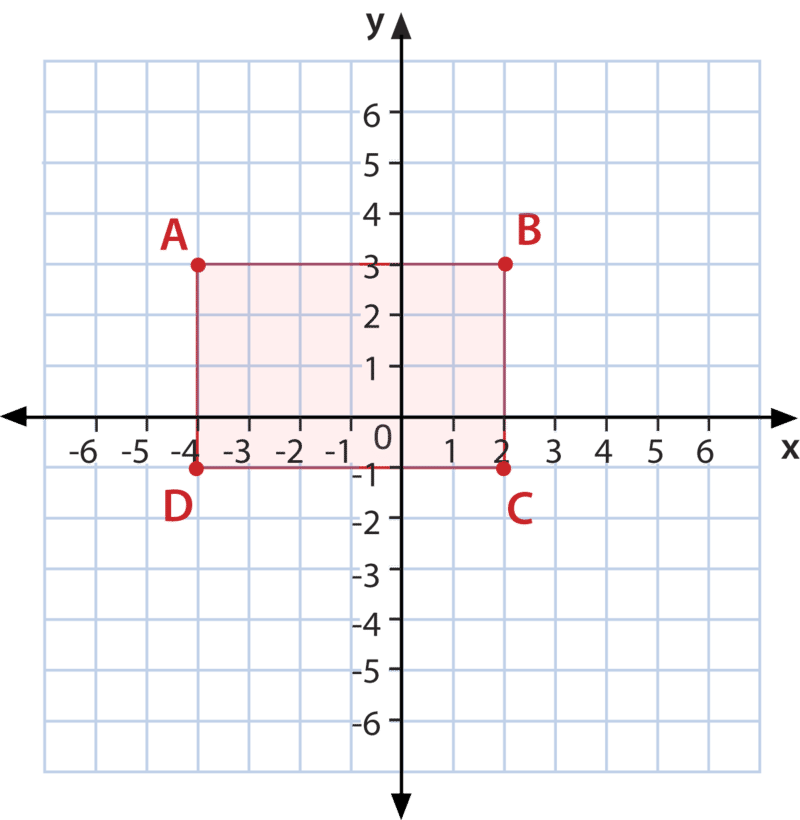 Малюнок\(\PageIndex{3}\)
Малюнок\(\PageIndex{3}\)Далі, для того щоб визначити, що це за форма, спочатку порахуйте кількість вершин.
Ця цифра має чотири, тому вона є однією з чотиригранних форм.
Потім подивіться, щоб побачити, скільки сторін рівні.
При цьому бічні\(AB=DC\) і\(AD=BC\). Так як існує два набори рівних сторін, це або прямокутник, або паралелограм.
Нарешті, перевірте кути.
У цій формі кути мають прямі кути, тому це прямокутник.
Ось ще один приклад.
Графік і назвіть наступну цифру з цими координатами\(D(1,3) E(5,3) F(7,−1) G(1,−1)\).
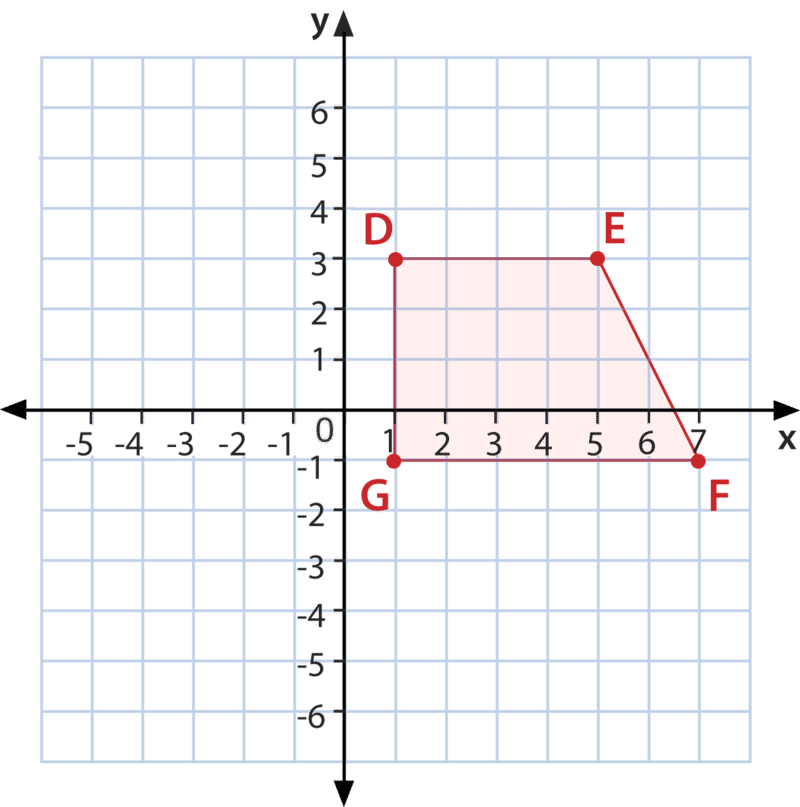 Малюнок\(\PageIndex{4}\)
Малюнок\(\PageIndex{4}\)Спочатку намітьте вершини і з'єднайте їх.
Далі порахуйте кількість вершин.
Їх чотири, так що це чотиригранна фігура, яку можна побачити по її формі.
Потім подивіться на боки.
Жодна зі сторін не має однакової довжини, тому така форма повинна бути трапецією.
Приклад\(\PageIndex{1}\)
Раніше вам дали проблему про Паркер та її панічну атаку математичного мистецтва.
Її вчитель мистецтва дає їй картину будівель в перспективі і каже їй розбити її на складові форми.
Рішення
Спочатку вона малює\(y\) -вісь вниз по центру задньої будівлі на малюнку, яка дивиться приблизно на півдорозі по всій картині. Потім вона малює\(x\) -вісь як лінію горизонту.
Далі вона примружилася до картини і намагається бачити її не як будівлі, а як форми, замість цього. У правій частині малюнка вона розуміє, що будівлі складають трикутник з однією вершиною, що починається з початку. А зліва від\(y\) -осі з іншого боку будівель зробіть ще один трикутник, також з вершиною біля початку. Навіть вулиця, розуміє вона, робить свій власний трикутник, знову ж з однією вершиною біля початку. А потім небо закінчує його четвертим трикутником з вершиною біля початку.
Потім вона бачить, що решта картини просто складається з прямокутників. Є один під вуличним трикутником, а один зліва будівлі. І той, де крихітна задня будівля.
Паркер робить висновок, що вона, можливо, зможе навчитися малювати зрештою.
Приклад\(\PageIndex{2}\)
Визначте форму, задану наступними вершинами.
\((−4,6)(4,6)(0,−6)\)
Рішення
Спочатку порахуйте кількість вершин.
В даному випадку існує три вершини. Якщо вершин три, то форма має три сторони.
Далі визначте, які форми можливі.
Існує лише одна замкнута форма з трьома сторонами, і це трикутник.
Відповідь - трикутник.
Приклад\(\PageIndex{3}\)
Визначте форму, задану наступними вершинами.
\((0,2)(2,0)(0,−3)\)
Рішення
Спочатку порахуйте кількість вершин.
В даному випадку існує три вершини. Якщо вершин три, то є три сторони.
Далі визначте, які форми можливі.
Існує лише одна замкнута форма з трьома сторонами, і це трикутник.
Відповідь - трикутник.
Приклад\(\PageIndex{4}\)
Визначте форму, задану наступними вершинами.
\((−1,−3)(−5,−3)(−7,1)(−1,1)\)
Рішення
Спочатку порахуйте кількість вершин.
В даному випадку вершин чотири. Якщо вершин чотири, то форма має чотири сторони.
Далі визначте, які форми можливі.
Чотиригранні фігури: квадрат, ромб, трапеція, прямокутник і паралелограм.
Потім нанесіть вершини на координатній площині.
Потім визначте властивості форми.
При цьому форма має дві паралельні лінії і дві непаралельні лінії. Єдина фігура з чотирьох сторін, в якій це так, є трапеція.
Відповідь - трапеція.
Приклад\(\PageIndex{5}\)
Визначте форму, задану наступними вершинами.
\((3,3)(0,3)(0,0)(3,0)\)
Рішення
Спочатку порахуйте кількість вершин.
В даному випадку вершин чотири. Якщо вершин чотири, то форма має чотири сторони.
Далі визначте, які форми можливі.
Чотиригранні фігури: квадрат, ромб, трапеція, прямокутник і паралелограм.
Потім нанесіть вершини на координатній площині.
Потім визначте властивості форми.
При цьому форма має два набори паралельних ліній і і всі сторони однакової довжини. Крім того, форма має чотири прямих кута. Квадрат - це форма, яка відповідає цим критерієм.
Відповідь - квадрат.
Рецензія
Графік кожної фігури, використовуючи вершини. Потім назвіть графічну фігуру.
- \(A(−2,2);B(2,2);C(2,−2);D(−2,−2)\)
- \(D(−4,3);E(−1,1);F(−4,1)\)
- \((1,1)(2,3)(4,1)\)
- \((−1,3)(−5,3)(−1,0)(−5,0)\)
- \((0,5)(3,5)(0,9)(3,9)\)
- \((0,6)(2,6)(0,10)(2,10)\)
- \((−3,6)(6,0)(9,0)\)
- \((−1,6)(−1,8)(−9,6)(−9,8)\)
- \((0,−8)(1,−5)(5,−5)(4,−8)\)
- \((12,0)(12,6)(7,0)\)
Для 11 - 15 намалюйте п'ять власних фігур на координатній сітці. Випишіть кожен набір координат і працюйте з партнером, щоб ідентифікувати кожну фігуру, використовуючи тільки координати.
Огляд (Відповіді)
Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 11.15.
Лексика
| Термін | Визначення |
|---|---|
| \(x\)-вісь | \(x\)-вісь - це горизонтальна вісь у координатній площині, зазвичай представляє значення вхідної або незалежної змінної. |
| вісь Y | \(y\)-вісь - це вертикальна числова лінія декартової площини. |
| Координати | Координати точки відображають розташування точки на декартовій площині. Координати записуються впорядкованими парами:\(x,y)\). |
| Замовлена пара | Впорядкована\(x,y)\) пара описує розташування точки на координатній сітці. |
| Походження | Походження - точка перетину осей x і y на декартовій площині. Координати походження є\((0, 0)\). |
| Квадранти | Квадрант - це одна четверта координатної площини. Чотири квадранти нумеруються за допомогою римських цифр I, II, III та IV, починаючи у верхньому правому куті та збільшуючись проти годинникової стрілки. |
Додаткові ресурси
Інтерактивний елемент
Відео: побудова точок на координатній площині
Практика: Класифікація багатокутників у координатній площині