8.5.1: Фундаментальна теорема числення

Фундаментальна теорема числення

Швидкість, обумовлена гравітацією, легко обчислюється за формулою: v = gt, де g - прискорення за рахунок сили тяжіння (9,8м/с ²) і t - час в секундах. Насправді, гідне наближення можна легко обчислити у вашій голові, округляючи 9,8 до 10, так що ви можете просто додати десятковий розряд до часу.

Використовуючи цю функцію для швидкості, як ви могли знайти функцію, яка представляла позицію об'єкта через певний час? А як щодо функції, яка представляла миттєве прискорення об'єкта в даний момент часу?

---

Фундаментальна теорема числення

Антипохідні

Якщо ви думаєте, що оцінка областей під кривими - це виснажливий процес, ви, мабуть, маєте рацію. На щастя, є більш простий метод. У цьому розділі наведемо загальний метод оцінки визначених інтегралів (площі під кривою) за допомогою антипохідних.

Визначення: Антидериватив Якщо F '(x) = f (x), то F' (x) вважається антипохідним f ( х).

Існують правила знаходження антипохідних простих силових функцій типу f (x) = x ². Коли ви читаєте їх, спробуйте подумати про те, чому вони мають сенс, маючи на увазі, що диференціація змінює інтеграцію.

Існують правила знаходження антипохідних простих силових функцій типу f (x) = x ². Коли ви читаєте їх, спробуйте подумати про те, чому вони мають сенс, маючи на увазі, що диференціація змінює інтеграцію.

Правила знаходження антипохідних силових функцій Правило влади де C - константа інтеграції, а n - раціональне число, яке не дорівнює -1. Постійна кратна правилу функції де k - константа. Правило суми та різниці Постійне правило
де k - константа. (Зверніть увагу, що це правило виникає в результаті правила влади вище.)

Фундаментальна теорема числення

Фундаментальна теорема числення робить зв'язок між похідними та інтегралами чітким. Інтеграція, що виконується на функції, може бути змінена диференціацією.

Фундаментальна теорема числення Якщо функція f (x) визначена через інтервал [a, b] і якщо F (x) є антидеративним від f на [a, b ], потім \ (\\ почати {вирівняний} \ int_ {a} ^ {b} f (x) d x =\ ліво.F (x)\ праворуч |_ {a} ^ {b} &\\ &= F (b) -F (a) \ кінець {вирівняний}\)

Ми можемо використовувати зв'язок між диференціацією та інтеграцією, викладену в фундаментальній теоремі числення, для більш швидкого обчислення певних інтегралів.

---

Приклади

Приклад 1

Оцініть\(\ \int_{1}^{2} x^{2} d x\).

Рішення

Цей інтеграл говорить нам оцінити площу під кривою\(\ f(x)=x^{2}\), яка є параболою через інтервал [1, 2], як показано на малюнку нижче.

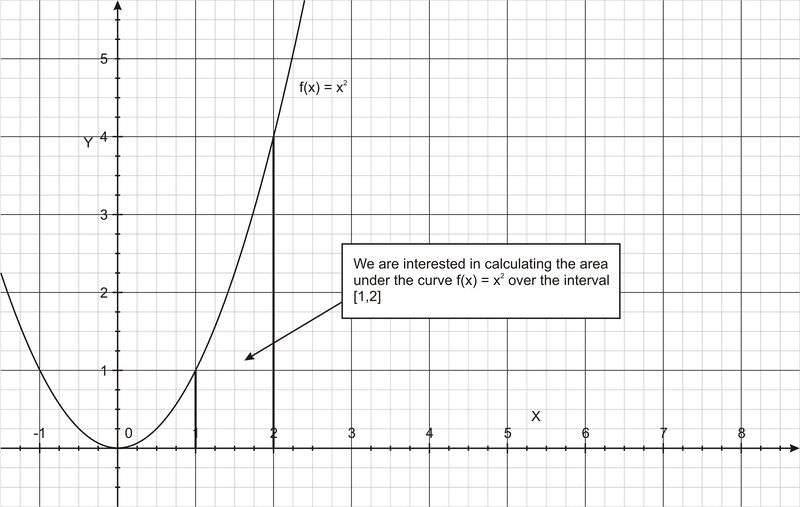
Щоб обчислити інтеграл відповідно до фундаментальної теореми числення, нам потрібно знайти антипохідну\(\ f(x)=x^{2}\). Виявляється\(\ F(x)=(1 / 3) x^{3}+C\), де С - константа інтеграції.

Як ми можемо це отримати? Подумайте про функції, які матимуть похідні від\(\ x^{2}\). Візьміть похідну,\(\ F(x)\) щоб перевірити, що ми знайшли таку функцію. (Більш конкретні правила див. у полі після цього прикладу). Підставляючи в фундаментальну теорему,

\(\ \int_{a}^{b} f(x) d x\)	\(\ =\left.F(x)\right|_{a} ^{b}\)
\(\ \int_{1}^{2} x^{2} d x\)	\(\ =\left[\frac{1}{3} x^{3}+C\right]_{1}^{2}\)
	\(\ =\left[\frac{1}{3}(2)^{3}+C\right]-\left[\frac{1}{3}(1)^{3}+C\right]\)
	\(\ =\left[\frac{8}{3}+C\right]-\left[\frac{1}{3}+C\right]\)
	\(\ =\frac{7}{3}+C-C\)
	\(\ =\frac{7}{3}\)

Таким чином, площа під кривою становить (7/3) одиниці ².

Приклад 2

Оцініть\(\ \int x^{3} d x\)

Рішення

З тих пір\(\ \int x^{n} d x=\frac{1}{n+1} x^{n+1}+C\), у нас є

\(\ \int x^{3} d x\)	\(\ =\frac{1}{3+1} x^{3+1}+C\)
	\(\ =\frac{1}{4} x^{4}+C\)

Щоб перевірити нашу відповідь, ми можемо взяти похідну\(\ \frac{1}{4} x^{4}+C\) і перевірити, що вона є\(\ x^{3}\), вихідна функція в нашому інтегралі.

Приклад 3

Оцініть\(\ \int 5 x^{2} d x\)

Рішення

Використовуючи постійну кратну правилу потужності, коефіцієнт 5 можна вивести за межі інтеграла:

\(\ \int 5 x^{2} d x=5 \int x^{2} d x\)

Тоді ми можемо інтегрувати:

\(\ =5 \cdot \frac{1}{2+1} x^{2+1}+C\)
\(\ =\frac{5}{3} x^{3}+C\)

Знову ж таки, якби ми хотіли перевірити нашу роботу, ми могли б взяти похідну\(\ \frac{5}{3} x^{3}+C\) і перевірити, що ми отримуємо\(\ 5 x^{2}\).

Приклад 4

Оцініть\(\ \int\left(3 x^{3}-4 x^{2}+2\right) d x\).

Рішення

Використовуючи правило суми та різниці, ми можемо розділити наш інтеграл на три інтеграли:

\ (\\ почати {масив} {l}
\ int\ лівий (3 x^ {3} -4 x^ {2} +2\ праворуч) d x =\\
3\ лівий (\ int x^ {3} d x\ праворуч) -4\ вліво (\ int x^ {2} d x\ праворуч) +\ лівий (\ int 2 d x\ праворуч)
\\ праворуч 3\ cdot\ frac {1} {4} x^ {4} -4\ cdot\ frac {1} {3} x^ {3} +2 x+c\ стрілка вправо\ розрив {3} {4} x^ {4} -\ frac {4} {3} x^ {3} +2 x+c
\ end {масив}\)

Приклад 5

Оцініть\(\ \int_{2}^{5} \sqrt{x} d x\).

Рішення

Оцінка цього інтеграла представляє обчислення площі під кривою\(\ y=\sqrt{x}\) від\(\ x = -2\) до\(\ x = 3\), показаний на малюнку нижче.

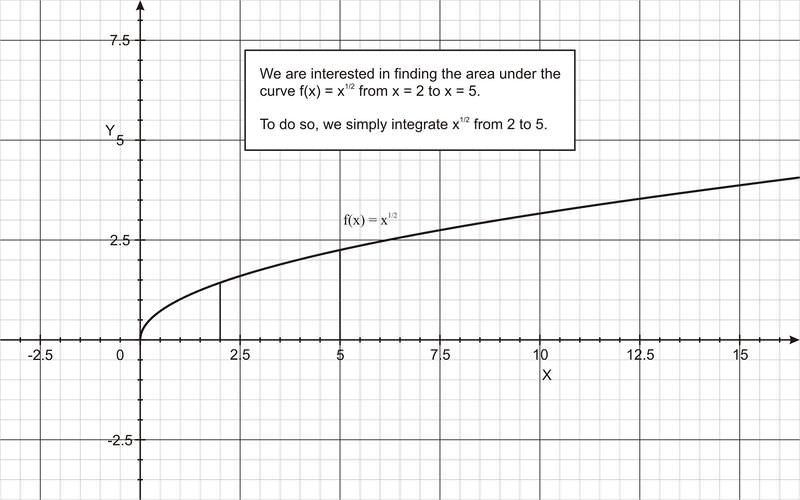
\(\ \int_{2}^{5} \sqrt{x} d x\)	\(\ =\int_{2}^{5} x^{1 / 2} d x\)
	\(\ =\left[\frac{1}{\frac{1}{2}+1} x^{1 / 2+1}\right]_{2}^{5}\)
	\(\ =\left[\frac{1}{3 / 2} x^{3 / 2}\right]_{2}^{5}\)
	\(\ =\frac{2}{3}\left[x^{3 / 2}\right]_{2}^{5}\)
	\(\ =\frac{2}{3}\left[5^{3 / 2}-2^{3 / 2}\right]\)
	\(\ =5.57\)

Так площа під кривою дорівнює 5,57.

приклад 6

Використовуйте фундаментальну теорему числення для вирішення:\(\ \int_{4}^{6} \frac{d x}{x}\).

Рішення

Враховуючи те, що ми знаємо, що якщо\(\ F(x)=\ln x\), то\(\ F^{\prime}(x)=\frac{1}{x}\)

Таким чином, застосуємо фундаментальну теорему числення:

\(\ \int-4^{6} \frac{d x}{x}=\ln x \mid-46\)

= Ф (6) - Ф (4) = [лн (6)] - [лн (4)] = 0,4055

приклад 7

Використовуйте фундаментальну теорему числення для вирішення:\(\ \int_{-2 p}^{2 p} 3 \cos (x) d x\).

Рішення

З огляду на те, що ми знаємо, що якщо F (x) = 3sin (x), то F '(x) = 3cos (x)

Отже, застосовуємо фундаментальну теорему числення:

\(\ \int_{-2 p}^{2 p} 3 \cos d x=\left.3 \sin (x)\right|_{-2 p} ^{2 p}\)

= Ф (8) - Ф (0) = [3сін (2р)] - [3сін (-2р)] = 1 - 0 = 0

---

Рецензія

Оцініть інтеграл:

1. Оцініть інтеграл\(\ \int_{0}^{3} 5 x d x\)
2. Оцініть інтеграл\(\ \int_{0}^{1} x^{4} d x\)
3. Оцініть інтеграл\(\ \int_{1}^{4}(x-3) d x\)

Знайдіть інтеграл:

4. Знайти інтеграл (х + 1) (2 х - 3) від -1 до 2.
5. Знайти інтеграл\(\ \sqrt{x}\) від 0 до 9.
6. Знайти\(\ \int_{-1}^{0}-3 d x\)
7. Знайти\(\ \int_{-1}^{3} d x\)
8. Знайти\(\ \int_{-p}^{\frac{p}{2}}-4 \cos (x) d x\)
9. Знайти\(\ \int_{0}^{2}-d x\)
10. Знайти\(\ \int_{2}^{7} \frac{d x}{x}\)
11. Знайти\(\ \int_{-2}^{0} x+5 d x\)
12. Знайти\(\ \int_{-p}^{\frac{3 p}{2}} 6 \sin (x) d x\)
13. Знайти\(\ \int_{6}^{7} \frac{d x}{x}\)

Киньте виклик собі:

14. Намалюйте\(\ y=x^{3}\) і\(\ y=x\) на тій же системі координат, а потім знайдіть площу області, укладеної між ними (а) в першому квадранті і (b) в першому і третьому квадрантах.
15. Оцініть інтеграл\(\ \int_{-R}^{R}\left(\pi R^{2}-\pi x^{2}\right) d x\), де R - константа.

---

Огляд (Відповіді)

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 8.13.

---

Лексика

Термін	Визначення
антидериватив	Антидериватив - це функція, яка змінює похідну. Функція A є антипохідною функції B, якщо функція B є похідною функції А.
похідний	Похідна функції - нахил прямої дотичної до функції в заданій точці на графіку. Позначення для похідних включають\(\ f^{\prime}(x), \frac{d y}{d x}, y^{\prime}, \frac{d f}{d x}\) і\(\ \frac{df(x)}{dx}\).
фундаментальна теорема числення	Фундаментальна теорема числення демонструє, що інтеграція, виконана на функції, може бути змінена диференціацією.
інтегральний	Інтеграл використовується для обчислення площі під кривою або площі між двома кривими.
теорема	Теорема - це твердження, яке можна довести правдивим за допомогою постулатів, визначень та інших теорем, які вже доведені.