Skip to main content
LibreTexts - Ukrayinska

1.3.1: Межі та асимптоти

  1. Last updated
  2. Save as PDF
  • Page ID
    55194

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Асимптоти та кінцева поведінка

    Більшість функцій продовжуються за межами вікна перегляду в нашому калькуляторі або комп'ютері. Люди часто малюють стрілку поруч з пунктирною лінією, щоб конкретно позначити візерунок. Як можна розпізнати ці асимптоти?

    Асимптоти та кінцева поведінка функцій

    Вертикальна асимптота - це вертикальна лінія, така як x = 1, яка вказує на те, де функція не визначена і все ж стає нескінченно близькою до.

    Горизонтальна асимптота - це горизонтальна лінія, така як y = 4, яка вказує, де функція згладжується, коли x стає дуже великим або дуже маленьким. Функція може торкатися або проходити через горизонтальну асимптоту.

    Реципрокна функція має два асимптоти, один вертикальний і один горизонтальний. Більшість комп'ютерів та калькуляторів не малюють асимптоти, тому їх потрібно вставляти вручну у вигляді пунктирних ліній.

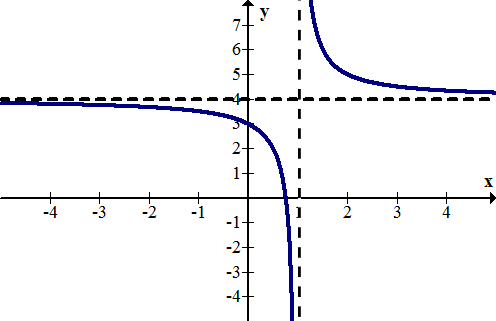    F-D_3FF266AF7EB8319649 FDD88C44E97225C3A3222D6645D8A4B77AEC3+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_png[Малюнок 1]

    Багато студентів мають помилкове уявлення про те, що асимптота - це лінія, до якої функція стає нескінченно близькою, але не торкається. Це неправда. Візьміть наступну функцію:

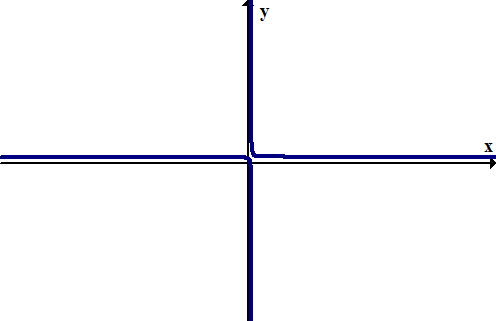
    F-D_1DD4D99D956D2F84A3F8FA8A1EBEA5B986C340F1deb746b5F95+зображення_thumb_поштова листівка_крихітка+зображення_thumb_поштова листівка_крихітка_png[Малюнок 2]

    Графік, здається, згладжується, коли x збільшується. Таким чином, горизонтальна асимптота дорівнює y=0, хоча функція чітко проходить через цей рядок нескінченну кількість разів.

    Причина, чому асимптоти важливі, полягає в тому, що коли ваша перспектива збільшена, асимптоти по суті стають графом.

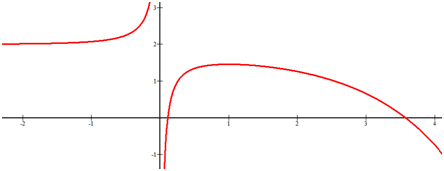
    F-D_A556БК6Ф215BE379D7B7F0292AD1259eb0f29b0f8bc716dc60695bfd9bfd9b+зображення_thumb_поштова листівка_крихіткий+зображення_великий палець_поштова листівка_крихітка_png[Малюнок 3]

    Щоб знайти асимптоти та кінцеву поведінку функції нижче, вивчіть, що відбувається з x та y, коли вони збільшуються або зменшуються.

    F-D_64A18C9FF04B462F61B779a6168F32E34F1CE72211F05CE1C0ce1AA+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихіткий.PNG[Малюнок 4]

    Функція має горизонтальну асимптоту y=2, оскільки x наближається до негативної нескінченності. Існує вертикальна асимптота при x = 0. Права сторона, здається, зменшується назавжди і не має асимптоти.

    Зверніть увагу, що похилі асимптоти існують і називаються косими асимптотами.

    Приклади

    Приклад 1

    Рішення

    Раніше вас запитали, як визначити асимптоти на графіку. Асимптоти, написані від руки, зазвичай ідентифікуються пунктирними лініями поруч з функцією, які вказують, як функція буде вести себе поза вікном перегляду. Рівняння цих вертикальних і горизонтальних пунктирних ліній мають вигляд x=. Коли задачі просять вас знайти асимптоти функції, вони запитують рівняння цих горизонтальних і вертикальних ліній.

    Приклад 2

    Визначте горизонтальні та вертикальні асимптоти наступної функції.

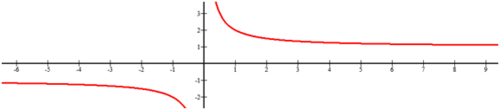    F-D_8ФБ54Б604C60F197659 FF184d40255dc8807b3E0F3A48764BB86DF15+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_png[Малюнок 5]

    Рішення

    Існує вертикальна асимптота при x = 0. Оскільки x стає нескінченно малим, існує горизонтальна асимптота у y=−1. Оскільки x стає нескінченно великим, існує ще одна горизонтальна асимптота при y = 1.

    Приклад 3

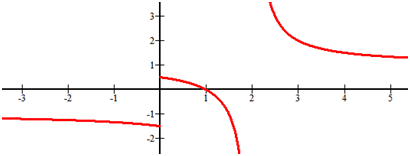
    Визначте горизонтальні та вертикальні асимптоти наступної функції.

    F-D_7725B28E779BDC7336222 Додати C7825bdfda9e992fd427f5af23d5+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_png[Малюнок 6]

    Рішення

    Існує вертикальна асимптота при x = 2. Коли x стає нескінченно малим, існує горизонтальна асимптота у y=−1. Коли x стає нескінченно великим, існує горизонтальна асимптота при y = 1.

    Приклад 4

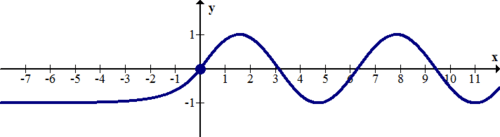
    Визначте горизонтальні та вертикальні асимптоти наступної кускової функції:

    \ (\ f (x) =\ лівий\ {\ begin {масив} {ll}
    e^ {x} -1 & x\ leq 0\\
    \ sin x & 0<x
    \ end {масив}\ вправо.\)

    F-D_6EF45EA28C6C6cd1DAA29C4BFF62A69a60ACF755F9052DE14B33E0+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_png[Малюнок 7]

    Рішення

    Існує горизонтальна асимптота у y=−1, оскільки x стає нескінченно малим. Це пов'язано з тим, що e підвищений до потужності дуже невеликого числа стає 0.000000... і в основному стає нулем.

    Приклад 5

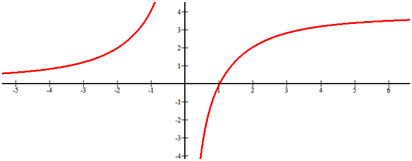
    Визначте асимптоти та кінцеву поведінку наступної функції.

    F-D_3779339C2394F6219F1F71A98342161d1d9A133ec85C0E4780E1FFCE+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_png[Малюнок 8]

    Рішення

    Існує вертикальна асимптота при x = 0. Поведінка кінця правої та лівої частини цієї функції не збігається. Горизонтальна асимптота, коли x наближається до негативної нескінченності, дорівнює y = 0, а горизонтальна асимптота, коли x наближається до позитивної нескінченності, дорівнює y На даний момент ви можете оцінити ці висоти лише тому, що вам не було надано функції або інструменти для аналітичного пошуку цих значень.

    Рецензія

    Визначте асимптоти та кінцеву поведінку наступних функцій.

    1. у = х

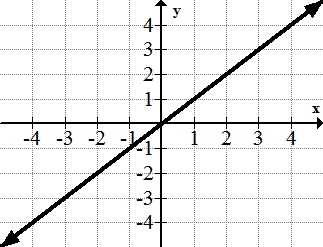    F-D_9D4D571A4A162C82505828012A72CAE83FF9C69945C19406E758C44+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_[Малюнок 9]

    2. р = х 2

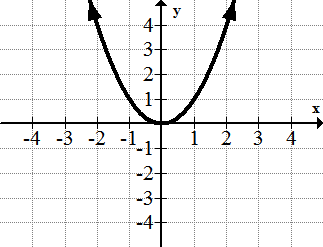    F-D_78D5440C5937a68366127AAE7E719A4D9F93042D3BAB1F89569F1C3+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_png[Малюнок 10]

    3. р = х 3

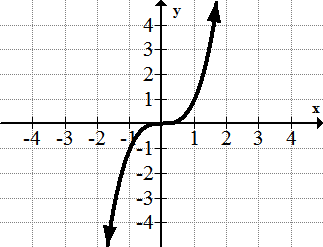    F-D_5ACE 471B4FAB230A7BD1AE3675F67C93FFFFE31804833AEBC53750B05+зображення_thumb_поштова листівка_крихітка+зображення_thumb_поштова листівка_крихітка_png[Малюнок 11]

    4. y=\(\ \sqrt{x}\)

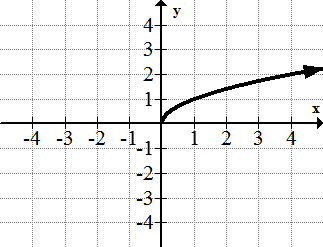    F-D_BE81d3C058586D2ec09a0de76d16d9378E5E16d3B775FBB96B32AE56+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_png[Малюнок 12]

    5. у =\(\ 1\over 2\)

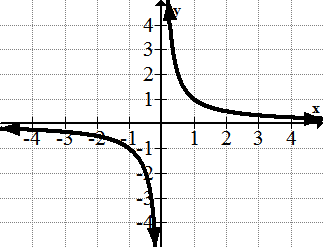    F-D_9ФД304Ф83С79А08ДА 85ФК0549Ф5039577С6СБ9099Б6С760073EB+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_png[Малюнок 13]

    6. р=е х

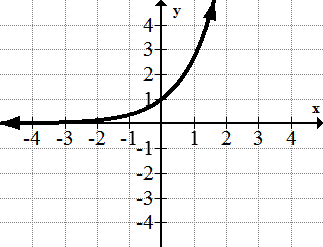    F-D_CE2F02AD61CDE6A338E7E1F784AF3004137C4BB8E46E4900997BAA6F+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_png[Малюнок 14]

    7. у = лн (х)

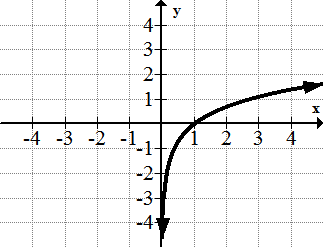    F-D_51b3B07a502 ACCB3C0C0EF532FF852E463816C1FE4028A7AABE84FCF+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_png[Малюнок 15]

    8. \(\ y=\frac{1}{1+e^{-x}}\)

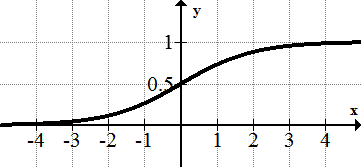    F-D_4503151956E3B3742D49327560551 DE2E49Ceda3B611B8A9DDCeb9A+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_png[Малюнок 16]

    9.

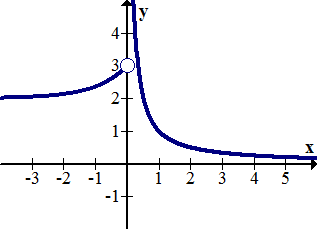    F-D_42F4E11F76E4D8BB1ФБА9ФДК8Б5354А192Ф2325320BB0DB1D57154AF+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_png[Малюнок 17]

    10.

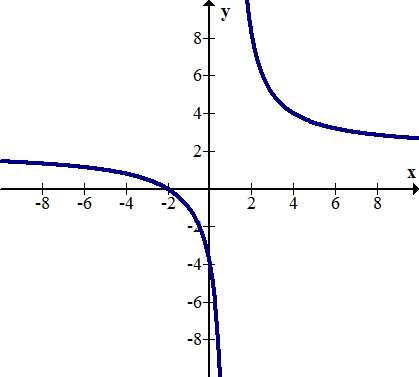    F-D0C5AEE26E06955973C0478 BE6996E4515D4A8519E505FA69F1B81BD+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_png[Малюнок 18]

    11.

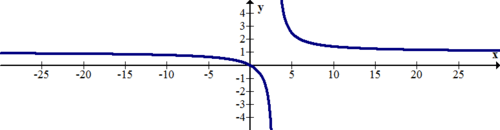    F-D_3FE1708893711C8CEB7CDC082198956704FDBC17B645E9E5DAE1F249+зображення_thumb_поштова листівка_крихітка_зображення_великий палецька_листівка_крихіткий.PNG[Малюнок 19]

    12. Вертикальні асимптоти виникають при значеннях x, де функція не визначена. Поясніть, чому має сенс, що\(\ y=\frac{1}{x}\) має вертикальну асимптоту при x = 0.

    13. Вертикальні асимптоти виникають при значеннях x, де функція не визначена. Поясніть, чому має сенс, що\(\ y=\frac{1}{x+3}\) має вертикальну асимптоту при x = −3.

    14. Використовуйте техніку з попередньої задачі для визначення вертикальної асимптоти функції\(\ y=\frac{1}{x-2}\).

    15. Використовуйте техніку з задачі #13 для визначення вертикальної асимптоти функції\(\ y=\frac{2}{x+4}\)

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 1.9.

    Лексика

    Термін Визначення
    Асимптотичний Функція є асимптотичною до заданого рядка, якщо даний рядок є асимптотою функції.
    Горизонтальна асимптота Горизонтальна асимптота - це горизонтальна лінія, яка вказує, де функція згладжується, оскільки незалежна змінна стає дуже великою або дуже маленькою. Функція може торкатися або проходити через горизонтальну асимптоту.
    коса асимптота Коса асимптота - це діагональна лінія, що позначає певний діапазон значень, до якого графік функції може наблизитися, але, як правило, ніколи не досягати. Коса асимптота існує, коли чисельник функції рівно на один ступінь більше знаменника. Коса асимптота може бути виявлена через довгий поділ.
    Косий асимптот Коса асимптота - це діагональна лінія, що позначає певний діапазон значень, до якого графік функції може наблизитися, але, як правило, ніколи не досягати. Коса асимптота існує, коли чисельник функції рівно на один ступінь більше знаменника. Коса асимптота може бути виявлена через довгий поділ.
    Кусково функція Кусково функція - це функція, яка об'єднує дві або більше частин інших функцій для створення нової функції.
    похила асимптота Похила асимптота - це діагональна лінія, що позначає певний діапазон значень, до якого графік функції може наблизитися, але ніколи не досягне. Схильна асимптота існує, коли чисельник функції рівно на один градус більше знаменника. Похила асимптота може бути виявлена через довгий поділ.
    Вертикальна асимптота Вертикальна асимптота - це вертикальна лінія, що позначає певне значення, до якого графік функції може наблизитися, але ніколи не досягне.

    Атрибуції зображень

    1. [Рисунок 1]
       Кредит: CK-12 Фонд
      Джерело: https://commons.wikimedia.org/wiki/File:Boston_Police_Special_Operations_Unit.jpg
       Ліцензія: CC BY-SA
    2. [Рисунок 2]
       Кредит:
       Ліцензія Фонду CK-12: CC BY-SA
    3. [Рисунок 3]
       Кредит: CK-12
      Ліцензія Фонду: CC BY-SA
    4. [Рисунок 4]
       Кредит:
       Ліцензія Фонду CK-12: CC BY-SA
    5. [Рисунок 5]
       Кредит: CK-12 Фонд
      Джерело: https://commons.wikimedia.org/wiki/File:Boston_Police_Special_Operations_Unit.jpg
       Ліцензія: CC BY-SA
    6. [Рисунок 6]
       Кредит: CK-12
      Ліцензія Фонду: CC BY-SA
    7. [Рисунок 7]
       Кредит: CK-12
      Ліцензія Фонду: CC BY-SA
    8. [Малюнок 8]
       Кредит:
       Ліцензія Фонду CK-12: CC BY-SA
    9. [Малюнок 9]
       Кредит: CK-12
      Ліцензія Фонду: CC BY-SA
    10. [Малюнок 10]
       Кредит:
       Ліцензія Фонду CK-12: CC BY-SA
    11. [Малюнок 11]
       Кредит: CK-12 Фонд
      Джерело: http://classconnection.s3.amazonaws.com/753/flashcards/449753/png/screen_shot_2011-09-21_at_8.07.32_pm1316650094429.png
      Ліцензія: CC BY-SA
    12. [Малюнок 12]
       Кредит:
       Ліцензія Фонду CK-12: CC BY-SA
    13. [Малюнок 13]
       Кредит:
       Ліцензія Фонду CK-12: CC BY-SA
    14. [Рисунок 14]
       Кредит:
       Ліцензія Фонду CK-12: CC BY-SA
    15. [Малюнок 15]
       Кредит:
       Ліцензія Фонду CK-12: CC BY-SA
    16. [Малюнок 16]
       Кредит: Фонд CK-12; Паула Еванс; Роб Янг
      Джерело: https://www.flickr.com/photos/rob-young/1149735229/; https://commons.wikimedia.org/wiki/File:Will_%26_Grace_ Квартир_будинок_ (1149735229) .jpg
      Ліцензія: CC BY-SA; CC BY-NC-SA
    17. [Рисунок 17]
       Кредит: CK-12
      Ліцензія Фонду: CC BY-SA
    18. [Рисунок 18]
       Кредит: CK-12
      Ліцензія Фонду: CC BY-SA
    19. [Малюнок 19]
       Кредит:
       Ліцензія Фонду CK-12: CC BY-SA