20.1: Затемнення

Last updated
Save as PDF

Page ID: 56416

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

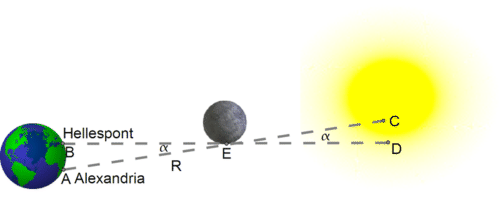
У повному затемненні Сонця Місяць просто ледь прикриває Сонце. Саме Сонце настільки віддалене, що при погляді з будь-якої точки Землі воно охоплює практично один і той же ділянку неба, шириною близько 0,5 градуса. Гіппарх сконцентрувався на точці Е на краю Місяця (малюнок), яка під час сукупності, якщо дивитися з Хеллеспонт (точка Б) якраз перекривала точку D на краю Сонця.

Якщо дивитися з Олександрії (точка А), в той самий момент точка Е перекривала лише точку С на Сонці, приблизно 1/5 сонячного діаметра коротше краю - саме тому затемнення там не було повним. П'ята частина діаметра Сонця охоплює близько 0,1 градуса в небі, тому малий кут\(\alpha\) (альфа, грецький A) між двома напрямками вимірюється приблизно 0,1 градуса. Цей кут є паралакс (Див. Розділ «Parallax») краю Місяця, розглядається з двох вище місць.

Навряд чи Гіппарх знав відстань АВ, але він напевно знав широти Геллеспонт і Олександрії. Місцева широта може бути показана рівною висоті небесного полюса над горизонтом, і сьогодні можна легко вивести, спостерігаючи висоту Полярної зірки над горизонтом. За часів Гіппарха полюс небес не був поблизу Поляріса (через прецесію рівнодення), але Гіппарх, який зіставив на карту позиції близько 850 зірок, мабуть, добре знав своє становище.

Широта Hellespont (від сучасного атласу) становить близько 40 щоб ^20′ (40 градусів і 20 хвилин, 60 хвилин на градус), в той час як Александрія є про ³¹ щоб 20′, різниця в 9 градусів. Ми також припустимо, що Олександрія точно належить на південь. Крім того\(r\), якщо радіус Землі, то окружність Землі є\(2\pi r\). Так як окружність також охоплює 360 градусів, отримуємо\[AB\,=\,\frac{2\pi r}{360}\times 9\]