20.3: Огляд лінійної алгебри

Last updated
Save as PDF

Page ID: 5238

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Наша мета цього розділу - нагадати вам про деякі поняття, які ви вивчили у своєму класі лінійної алгебри. Це не означає, щоб бути детальною прогулянкою. Якщо ви хочете дізнатись більше про будь-яке з наступних понять, я рекомендую підібрати книгу лінійної алгебри та прочитати з цього розділу. Але це послужить хорошим нагадуванням і відміткою понять, які важливі для нас в цьому розділі.

Власні вектори

Задана квадратна матриця A\((m \times m)\), власний вектор v є розв'язком наступного рівняння.

\[A v=\lambda v \nonumber \]

Іншими словами, якщо ми помножимо матрицю на цей вектор, ми змінюємо лише наше положення паралельно вектору (ми повертаємо масштабовану версію вектора v).

І\(\lambda\) (скільки масштабується вектор v) називається власним значенням.
Отже, скільки власних значень є щонайбільше? Давайте зробимо перші кроки до вирішення цього рівняння.

\[A v=\lambda v \Rightarrow(A-\lambda I) v=0 \nonumber \]
що має ненульові рішення, коли\(|A-\lambda I|=0\). Тобто рівняння m-го порядку, в\(\lambda\) якому може бути не більше m різних розв'язків. Пам'ятайте, що ці рішення можуть бути складними, навіть якщо A є реальним.

Векторне розкладання

Оскільки власні вектори утворюють безліч усіх основ, вони повністю представляють простір стовпців. Враховуючи це, ми можемо розкласти будь-який довільний вектор x на комбінацію власних векторів.

\[x=\sum_{i} c_{i} v_{i} \nonumber \]

Таким чином, коли ми множимо вектор з матрицею A, ми можемо переписати його через власні вектори.

\ [\ begin {масив} {c}
А = А\ ліворуч (c_ {1} v_ {1} +c_ {2} v_ {2} +\ ldots\ праворуч)\\
A x=c_ {1} A v_ {1} +c_ {2} A_ {v} 2+\ ldots\
A x = c_ {1}\ lambda_ {1} v_ {1} +c_ {2}\ лямбда_ {2} v_ {2} +c_ {3}\ lambda_ {3} v_ {3} +\ ldots
\ end {масив}\ nonumber\]
Отже, дія A on x визначається власними значеннями та власними векторами. І ми можемо спостерігати, що малі власні значення мають невеликий eect на множення.

Чи знаєте ви?

• Для симетричних матриць власні вектори для різних власних значень є ортогональними.

• Всі власні значення дійсної симетричної матриці є дійсними.
• Всі власні значення додатної напіввизначеної матриці є невід'ємними.

Діагональне розкладання

Також відомий як Eigen розкладання. Нехай S — квадратна\(m \times m \) матриця з m лінійно незалежними власними векторами (недефектна матриця).

Потім існує декомпозиція (теорема матричної цифровізації)\[ S=U \Lambda U^{-1} \nonumber \]

Де стовпці U - власні вектори S. І\(\Lambda\) - діагональна матриця з власними значеннями в її діагоналі.

Декомпозиція сингулярних значень

Часто декомпозиція сингулярних значень (SVD) використовується для більш загального випадку факторизації\(m \times n\) неквадратної матриці:

\[\mathbf{A}=\mathbf{U} \boldsymbol{\Sigma} \mathbf{V}^{T}\]

де U -\(m \times m \) матриця, що представляє ортогональні власні вектори AA ^_T, V -\(n \times n \) матриця, що представляє ортогональні власні вектори A, ^T A, а V -\(n \times n\) матриця, що представляє квадратні корені власних значень A ^T A (званих сингулярними значеннями А):

\[ \mathbf{\Sigma}=\operatorname{diag}\left(\sigma_{1}, \ldots, \sigma_{r}\right), \sigma_{i}=\sqrt{\lambda_{i}} \]

SVD будь-якої заданої матриці можна обчислити однією командою в Matlab, і ми не будемо охоплювати технічні деталі її обчислення. Зверніть увагу, що отримана «діагональна» матриця\(\mathbf{\Sigma} \) може бути не повноранговою, тобто вона може мати нульові діагоналі, а максимальна кількість ненульових сингулярних значень - min (m, n).

Наприклад, нехай

\ [A=\ left [\ begin {масив} {cc}
1 & -1\\
1 & 0\
1 & 0
\ end {масив}\ праворуч]\ nonumber\]

таким чином m = 3, n = 2. Його СВД є

\ [\ лівий [\ початок {масив} {ccc}
0 &\ frac {2} {\ sqrt {6}} &\ frac {1} {\
sqrt {3}}\\ frac {1} {\ sqrt {2}} & -\ frac {1} {\ sqrt {3}}\ frac {1} {
\ sqrt {2}} &\ frac {1} {\ sqrt {6}} & -\ frac {1} {\ sqrt {3}}
\ кінець {масив}\ праворуч]\ лівий [\ почати {масив} {cc}
1 &
0\\ 0 &\\ sqrt {3}
\\
0 & 0\ кінець {масив}\ справа]\ лівий [
\ початок {масив} {cc}\ frac {1} {\ sqrt {2}} &
\ frac {1} {\ sqrt {2} {1} {\ sqrt {2}}
\ кінець {масив}\ праворуч]\ nonumber\]

Зазвичай сингулярні значення розташовуються в порядку спадання.

SVD широко використовується в статистичному, числовому аналізі та методах обробки зображень. Типовим застосуванням СВД є оптимальне низькорангове наближення матриці. Наприклад, якщо у нас є велика матриця даних, наприклад 1000 на 500, і ми хотіли б наблизити її до матриці нижчого рангу без великої втрати інформації, сформульована як наступна задача оптимізації:

Знайти A _k рангу k такий, що\(\mathbf{A}_{k}=\min _{\mathbf{X}: r a n k(\mathbf{X})=k}\|\mathbf{A}-\mathbf{X}\|_{F} \)

де індекс F позначає норму Фробеніуса\(\|\mathbf{A}\|_{F}=\sqrt{\sum_{i} \sum_{j}\left|a_{i j}\right|^{2}}\). Зазвичай k набагато менший за r Розв'язком цієї задачі є SVD X\(\mathbf{U} \boldsymbol{\Sigma} \mathbf{V}^{T}\), з найменшими r-k сингулярними значеннями,\(\mathbf{\Sigma}\) встановленими нулем:

\[\mathbf{A}_{k}=\operatorname{Udiag}\left(\sigma_{1}, \ldots, \sigma_{k}, \ldots, 0\right) \mathbf{V}^{T} \nonumber \]

Таке наближення може бути показано, що має похибку\(\left\|\mathbf{A}-\mathbf{A}_{k}\right\|_{F}=\sigma_{k+1}\). Це також відоме як теорема Еккарта-Янга.

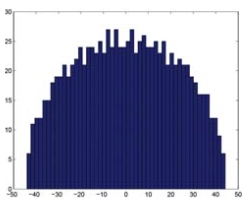
Загальним застосуванням SVD для мережевого аналізу є використання розподілу сингулярних значень матриці суміжності для оцінки того, чи виглядає наша мережа випадковою матрицею. Оскільки розподіл сингулярних значень (закон півкола Вігнера) та найбільшого власних значень матриці (розподіл Трейсі-Відома) були теоретично виведені, можна вивести розподіл власних значень (сингулярних значень у SVD) спостережуваної мережі (матриці) та обчислити p- значення для кожного з власних значень. Тоді нам потрібно лише подивитися на значні власні значення (сингулярні значення) та відповідні їм власні вектори (сингулярні вектори), щоб дослідити значущі структури в мережі. На наступному малюнку показано розподіл сингулярних значень випадкового гауссового унітарного ансамблю (GUE, див. Це посилання Вікіпедії для визначення та властивостей en.wikipedia.org/wiki/random_matrix) матриці, які утворюють півколо відповідно до закону півкола Вігнера (рис. 20.4).

Приклад використання SVD для виведення структурних шаблонів у матриці або мережі наведено на малюнку 20.5. У верхній лівій панелі показано структуру (червону), додану до випадкової матриці (синій фон на тепловій карті), що охоплює перший рядок і перші три стовпці. SVD виявляє це шляхом ідентифікації великого сингулярного значення (обведеного червоним кольором при розподілі сингулярних значень) та відповідних великих навантажень рядків (U1), а також трьох великих завантажень стовпців (V1). Оскільки до мережі додається більше структур (верхня права та нижня панелі), їх можна виявити за допомогою SVD, переглянувши наступні найбільші сингулярні значення та відповідні завантаження рядків/стовпців тощо.