Skip to main content
LibreTexts - Ukrayinska

5.3: Цілочисельна оптимізація для управління інфраструктурою

  1. Last updated
  2. Save as PDF
  • Page ID
    9149

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    У багатьох задачах оптимізації управління інфраструктурою змінні рішення можуть бути обмежені цілими значеннями. Наприклад, у попередньому розділі змінні рішення були визначені як здійснення конкретної дії з технічного обслуговування або реабілітації j на сегменті дорожньої частини i Хоча змінна рішення може бути часткою, так що тільки частина сегмента дорожньої частини піддається технічному обслуговуванню, це більш природним для управління сегментом в цілому і бажають мати двійкові змінні рішення, які дорівнюють нулю або одиниці.

    Цілочисельні обмеження накладають кілька проблем при отриманні оптимальних розв'язків. Для лінійного програмування оптимальні значення можна шукати на крайніх кутах можливої області. При обмеженнях цілочисельних значень оптимальне рішення може знаходитися всередині допустимої області. Як показано на малюнку 5.3.1, можливі цілочисельні значення показані у вигляді точок у межах області, що задовольняє лінійним обмеженням. Єдиним здійсненним рішенням на крайньому куті буде рішення\(x1 = 0\) і\(x2 = 0\). Точка А, позначена на малюнку, матиме дробові значення\(x1\) і\(x2\).

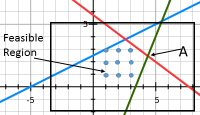
    clipboard_ea8f6a2f616ecfec02cc3e0ba4cec95b5.png
    Рисунок\(\PageIndex{1}\): Ілюстрація цілочисельних можливих розв'язків задачі лінійної оптимізації.

    Один з підходів до цілочисельного програмування полягає в ігноруванні цілочисельних обмежень і вирішенні задачі як лінійної програми. З двійковими обмеженнями та цілочисельними параметрами та значеннями обмежень цей підхід часто працює, щоб дати оптимальні двійкові рішення. Дробове значення змінної рішення може бути округлено менеджером, щоб отримати дуже хороше, але не обов'язково строго оптимальне рішення в цьому підході. Враховуючи невизначеність у витратах та ефектах дій, округлення може не вплинути на загальну продуктивність інфраструктури.

    Існують і більш формальні методи отримання оптимальних цілочисельних розв'язків. Популярним підходом є «гілка та прив'язка». У цьому процесі виходить початкове лінійне рішення, а потім додаються обмеження, щоб змусити рішення бути цілим числом. Наприклад, на малюнку 5.3.1, якщо точка А була отримана як оптимальне рішення, і хорошим додатковим обмеженням може бути\(x1\) потрібно 3 або менше:\(x1 \leq 3\). Це буде нова «гілка» для вирішення проблеми з «зв'язкою», яка вирізає частину області, яка не містить цілих значень. Додавання обмежень таким чином триватиме до тих пір, поки не буде отримано цілозначне оптимальне рішення.

    «Відгалуження та межа» або інші цілі підходи до програмування є частиною найпопулярнішого програмного забезпечення для оптимізації, включаючи програму Solver для електронної таблиці EXCEL. Цілочисельні обмеження вказуються, коли задачі вводяться в програми. Однак рішення цілочисельних програм вимагає більше часу обчислення, ніж лінійні програми порівнянного розміру. Хоча лінійні програми з тисячами змінних рішень можуть бути легко вирішені, цілочисельні програми можуть бути реалістично обмежені сотнями змінних рішень. Тим не менш, це цілком може стати корисним діапазоном для багатьох проблем управління інфраструктурою.

    Задача «комівояжера» є класичним прикладом цілочисельної задачі програмування. Проблема полягає в тому, щоб розробити тур туди і назад , який відвідує кожен з набору міст рівно один раз з мінімальною відстанню подорожі. Для управління інфраструктурою екскурсія такого типу може бути сформульована інспектором різних компонентів інфраструктури або працівником з технічного обслуговування з набором призначених робочих місць. У цих проблемах «міста» були б інспекції або місця роботи. Програмне забезпечення маршрутизації UPS для вантажівок доставки, згадане у вступі до цього розділу, вирішує цю проблему (UPS 2016). Варіації проблеми можна знайти у виробництві (де «міста» можуть бути плями на чіпі) та секвенування ДНК.

    Змінна рішення для проблеми комівояжера може бути 0 \(x_{ij}\), якщо поїздка від\(i\) до не\(j\) є в турі, і 1, якщо поїздка від\(i\) до\(j\) знаходиться в турі. Метою функції було б підсумувати відстань (або вартість) поїздки від\(i\) до,\(j\) помножену на\(x_{ij}\) значення. Тільки ті поїздки, які є частиною туру, понесуть будь-яку відстань і вплинуть на значення цільової функції. Обмеження вимагають, щоб з кожного міста був рівно один виліт (тому сума\(x_{ij}\) від I дорівнює одиниці) і рівно по одному прибуттю в кожне місто. Додаткові обмеження необхідні для того, щоб тур був завершеним (тобто тур не має декількох нероз'єднаних контурів). Нарешті, змінні рішення \(x_{ij}\) обмежені нулем або одиницею.

    Для задачі комівояжера розроблено численні спеціалізовані алгоритми. На практиці евристичні підходи можуть отримати дуже хороші (але не обов'язково оптимальні) рішення.