5.2: Лінійна оптимізація для управління інфраструктурою

Проблеми з постійними змінними рішеннями та лінійними обмеженнями та об'єктивними функціями є дуже поширеними та привернули значну увагу досліджень. Ці задачі вирішуються за допомогою алгоритмів лінійного програмування, таких як метод симплекса. Типове програмне забезпечення може вмістити тисячі змінних рішень та обмежень.

Формально лінійна програма представлена у вигляді:

\[ \text{Maximize c} * \text{x subject to A x} =\text{y and x} \geq 0 \]

Де c - вектор параметрів, x - вектор неперервних змінних рішення, A - матриця параметрів і y - вектор параметрів обмеження. Ця формулювання може вмістити обмеження нерівності з додаванням змінних рішень, що представляють слабкість у обмеженнях. Наприклад, обмеження\(x1 + x2 ≤ 5\) (показано на малюнку 5.2.1) буде переписано як\(x1 + x2 + x3 = 5 \) і додатне значення x3 в оптимальному рішенні вказувало б на те, що обмеження не є обов'язковим. Аналогічно змінні рішення можуть приймати будь-яке значення (як негативне, так і позитивне) з додаванням змінних рішення. На практиці програмне забезпечення лінійного програмування може приймати як вхідні нерівності, так і необмежені змінні рішення і перетворювати задачу в стандартну форму ур. 5.2.1.

Лінійна програма має три типи можливостей вирішення:

• Рішення неможливе. Прикладом може бути: Максимізувати змінну рішення x з урахуванням обмежень x < 1 and x > 5. Жодне значення x не задовольнить обидва обмеження. Для управління інфраструктурою прикладом може бути, якщо бюджет недостатній для досягнення необхідних функціональних умов.
• Існує єдине оптимальне рішення. Наприклад, проблема управління дорожнім полотном може полягати в тому, щоб максимізувати середній стан сегментів дорожнього полотна з урахуванням бюджетних обмежень. Як правило, буде визначено комплекс заходів з технічного обслуговування (наприклад, ремонт або ямковий ремонт) для підмножини сегментів дорожнього полотна, який повністю використовує бюджет. Більш великий приклад цієї проблеми наведено нижче.

Існує безліч оптимальних рішень. На малюнку 5.2.1 відрізок лінії між A і B включає нескінченну кількість оптимальних рішень, які є комбінаціями двох змінних рішення x1 і x2 для лінійної програми Maximize\( 2 * x1 + x2 \text { subject to } 2 * x1+x 2 \leq 4 \text {and } x 1, x 2 \text { both} \geq 0\). Допустимою областю є трикутна область АВО.

Малюнок\(\PageIndex{1}\): Ілюстрація декількох оптимальних рішень.

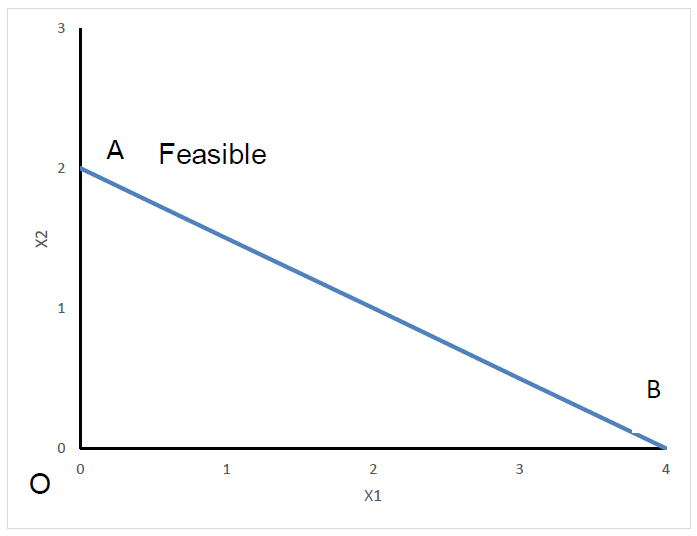
Лінійні програми володіють корисною властивістю того, що множина можливих розв'язків утворює опуклу область. «Доцільно» у цьому контексті означає комбінацію змінних рішень, які задовольняють обмеженням проблеми. Затінена область на малюнку 5.2.1 є можливою областю для x1 і x2. Затінена область є опуклою, оскільки відрізок лінії між будь-якими двома можливими комбінаціями x1 та x2 все ще буде в можливій області. Ця опуклість має два корисних значення. По-перше, будь-яке оптимальне рішення не буде локальним оптимумом, а буде глобальним оптимальним. Тобто, якщо ви знайдете комбінацію x1 і x2, для якої поліпшення неможливо від невеликих змін, то ніяка інша комбінація x1 і x2 з бути краще. По-друге, оптимальні значення змінних рішення для лінійної програмної задачі лягатимуть на межі допустимої області, наприклад, відрізка лінії на малюнку 5.2.1. Ця властивість використовується алгоритмом симплексного рішення для лінійних програм.

Симплексний метод є поширеним методом розв'язання задач лінійного програмування. Вона починається з «базового можливого рішення». З m обмеженнями та n змінними рішення базове можливе рішення складається з n-m змінних рішень, встановлених на нуль, а решта m змінних рішення - розв'язку m лінійних рівнянь обмеження. Симплексний метод перевіряє, чи можливо поліпшення шляхом обміну однієї з n-m змінних рішення, встановлених на нуль, зі змінною рішення в базовому здійсненному рішенні. Якщо можливо покращення, алгоритм робить цей перемикач, що еквівалентно «повороту» від однієї крайньої точки на опуклої здійсненної області до іншої. Повороти тривають до тих пір, поки таке поліпшення неможливо. Початкове базове можливе рішення можна отримати просто шляхом додавання «змінних штучного рішення», рівних значенню параметрів обмеження, а потім відкинувши від цих штучних змінних.

Технічне обслуговування та реабілітація дорожнього полотна є хорошим прикладом лінійного програмування, що застосовується для управління інфраструктурою. У цьому додатку дорожня мережа розділена на численні короткі ділянки, які можуть варіюватися від декількох кілометрів до окремих блоків у міській мережі (з індексом I від 1 до n сегментів). Можливі дії з технічного обслуговування визначені для ділянок дорожнього полотна, такі як заповнення вибоїн (j = 1), перемощення (j = 2) або нічого не робити (j = 3). Витрати на кожну дію для кожної ділянки тротуару потім оцінюються, як правило, виходячи з площі ділянки тротуару (\(p_{ij}\)). Стан кожної ділянки дорожнього покриття прогнозується за умови, що виконується одна дія (заповнення вибоїн, перемощення або нічого не робити в цьому прикладі) (\(c_{ij}\)де більш бажані нижчі значення\(c_{ij}\)). Потім визначається бюджетне обмеження для дій та об'єктивна функція (наприклад, максимізація середнього стану системи). В результаті виходить задача лінійного програмування:

\[ \text {Minimize } \sum i \sum j \frac{x_{i j^{*}} c_{i j}}{n} \]

\[ \text {subject to } \sum j x_{i j}=1 \text { for all } i\]

\[ \sum i \sum j \quad x_{i j} * p_{i j} \leq B\]

\[ x_{i j} \leq 0 \text { for all } i, j \]

Де\(x_{ij}\) діє\(j\) на секції I,\(c_{ij}\) прогнозується умова з дією\(j\) на ділянці I, n - кількість сегментів дорожньої частини,\(p_{ij}\) вартість дій\(j\) на сегменті I і B - загальне бюджетне обмеження.

Теоретично, в цій формулюванні\(x_{ij}\) можуть приймати неціле значення між 0 і 1, але на практиці майже всі оптимальні\(x_{ij}\) будуть нуль або одиницю.

У базову формулювання ур. 5.2.2 до 5.2.6 можуть бути внесені різні модифікації. Для цільової функції (ур. 5.2.2) стан кожного сегмента може бути зважений кількістю трафіку та площею сегмента. Ці ваги призведуть до оптимального рішення для сприяння роботі на сильно пройдених дорогах та мінімізації середніх умов дорожньої частини, а не середніх умов сегмента, як у еквалайзері 5.2.2. Додаткові дії з технічного обслуговування дорожнього полотна можуть бути визначені для розширення обмеження ур. 5.2.3. Проблема може бути змінена шляхом визначення максимально допустимих умов як обмеження для кожного розділу, а потім мінімізації витрат на досягнення цього обмеження. Навіть не змінюючи цільової функції таким чином, при бажанні можна додати гранично допустимі обмеження умов.

Ця стратегія визначення дій щодо компонентів інфраструктури не обмежується сегментами дорожнього полотна. Для керівника військової бази або кампусу формулювання задачі в Рівняннях 5.2.2 - 5.2.5 може бути використано для дахів (з заміною або технічним обслуговуванням в якості дій), компонентів зливових вод, будівельних компонентів або ряду інших інфраструктурних систем.

При формулюванні задач лінійного програмування корисно вирішити ряд питань:

• Які мої можливі рішення? Як їх можна представити як змінні рішення?
• Яка моя мета? Чи можна це представити як лінійну функцію моїх змінних рішень?
• Які обмеження на вибрані значення змінних моїх рішень? Чи можуть вони бути представлені у вигляді лінійних функцій змінних рішень?

Постановка проблеми є складною, але є важливим кроком у будь-якій оптимізації. Дійсно, формулювання є більш складним, ніж рішення, оскільки існує багато хороших програмних програм, доступних для рішення.

Наступний приклад ілюструє використання питань формулювання.

Проблема: Припустимо, ви бажаєте мінімізувати витрати на доставку етанолу з набору виробничих потужностей з максимальним запасом виробництва Si, де i йде від 1 до n, до набору столичних нафтозмішувальних установок (оскільки етанол змішується з бензином) з необхідними кількостями,\(P_j\) де j йде від 1 до м Припустимо вартість транспортування від виробничого об'єкта до змішувальної установки становить\(C_{ij}\). Сформулюйте лінійну програмну задачу для обслуговування необхідного попиту з найменшими витратами.

• Які мої можливі рішення? Як їх можна представити як змінні рішення? Кількість етанолу, що відвантажується з кожного об'єкта постачання до кожного мегаполісу, буде моїм змінним рішення. Визначимо\(x_{ij}\) як кількість етанолу, що відвантажується з виробничого об'єкта.
• Яка моя мета? Чи можна це представити як лінійну функцію моїх змінних рішень? Постановка проблеми дає мету мінімізувати транспортні витрати. Об'єктивною функцією буде:\(\sum i \sum j c_{i j} * x_{i j}\) яка є загальною вартістю перевезення та є лінійною щодо змінних рішень.
• Які обмеження на вибрані значення змінних моїх рішень? Чи можуть вони бути представлені у вигляді лінійних функцій змінних рішень? Один набір обмежень полягає в тому, щоб етанол, що відвантажується з кожного виробничого об'єкта, не перевищував доступну пропозицію:\(\sum i x_{i j} \leq S_{i}\) для кожного\(i\). Другий набір обмежень полягає в забезпеченні задоволення попиту в кожному столичному районі:\(\sum i x_{i j} \geq P_{j}\) для кожного j мегаполісу. Нарешті, потоки повинні бути позитивними:\(x_{i j} \geq 0\).

Існують різноманітні програмні пакети, які можна використовувати для лінійного програмування. Наприклад, програма електронних таблиць EXCEL має рутину оптимізації під назвою Solver. Frontline Systems (2016) має підручник, доступний для використання Solver. Читачі, зацікавлені в більш поглибленому лікуванні лінійного програмування, можуть звернутися до відповідного підручника (Boyd and Vandenberghe, 2004).