13.5: Байєсівська теорія мережі

Вступ

Теорію байєсових мереж можна розглядати як злиття діаграм падіння та теореми Байєса. Байєсівська мережа, або мережа переконань, показує умовні ймовірності та причинно-наслідкові зв'язки між змінними. Імовірність події, враховуючи, що інша подія вже сталася, називається умовною ймовірністю. Імовірнісна модель якісно описується спрямованим ациклічним графом, або DAG. Вершини графа, які представляють змінні, називаються вузлами. Вершини представлені у вигляді кіл, що містять назву змінної. Зв'язки між вузлами називаються дугами, або ребрами. Краї малюються у вигляді стрілок між вузлами і представляють залежність між змінними. Тому для будь-яких пар вузлів вказують, що один вузол є батьківським іншим, тому немає припущень про незалежність. Припущення про незалежність маються на увазі в байєсівських мережах відсутністю зв'язку. Ось зразок DAG:

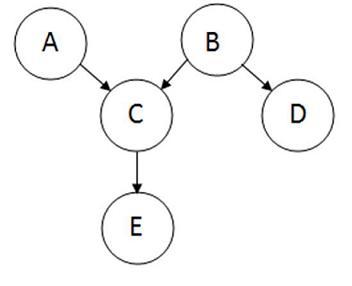
Вузол, де бере початок дуги, називається батьківським, тоді як вузол, де закінчується дуга, називається дочірнім. У цьому випадку A є батьком C, а C є дочірнім елементом A. вузли, які можуть бути досягнуті з інших вузлів, називаються нащадками. Вузли, які ведуть шлях до певного вузла, називаються предками. Наприклад, С і Е є нащадками А, а А і С - предками Е. У байєсівських мережах немає петель, так як жодна дитина не може бути власним предком або нащадком. Байєсівські мережі, як правило, також включають набір таблиць ймовірностей, вказуючи ймовірності для істинних/хибних значень змінних. Основним моментом Байєсівських мереж є можливість виконання ймовірнісного висновку. Це означає, що ймовірність кожного значення вузла в байєсівській мережі може бути обчислена, коли відомі значення інших змінних. Крім того, оскільки незалежність між змінними легко розпізнати, оскільки умовні відносини чітко визначені ребром графа, не всі спільні ймовірності в системі Байєса потрібно обчислити, щоб прийняти рішення.

Спільні розподіли ймовірностей

Спільна ймовірність визначається як ймовірність того, що ряд подій відбудеться одночасно. Спільна ймовірність декількох змінних може бути розрахована з добутку індивідуальних ймовірностей вузлів:

\[\mathrm{P}\left(X_{1}, \ldots, X_{n}\right)=\prod_{i=1}^{n} \mathrm{P}\left(X_{i} \mid \text { parents }\left(X_{i}\right)\right) \nonumber \]

Використовуючи вибірковий графік з введення, спільний розподіл ймовірностей становить:

\[P(A, B, C, D, E)=P(A) P(B) P(C \mid A, B) P(D \mid B) P(E \mid C) \nonumber \]

Якщо вузол не має батьківського вузла, наприклад вузла A, її розподіл ймовірностей описується як безумовний. В іншому випадку локальний розподіл ймовірності вузла умовний від інших вузлів.

Класи еквівалентності

Кожна байєсівська мережа належить до групи байєсівських мереж, відомих як клас еквівалентності. У заданому класі еквівалентності всі байєсівські мережі можуть бути описані одним і тим же спільним оператором ймовірності. Як приклад, наступний набір байєсівських мереж містить клас еквівалентності:

Мережа 1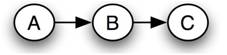

Мережа 2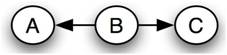

Мережа 3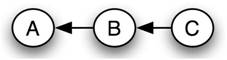

Причинність, що мається на увазі кожна з цих мереж, різна, але одне і те ж спільне твердження ймовірності описує їх усіх. Наступні рівняння демонструють, як кожна мережа може бути створена з того ж вихідного звіту ймовірності спільної:

Мережа 1

\[P(A, B, C)=P(A) P(B \mid A) P(C \mid B) \nonumber \]

Мережа 2

\[\begin{align*} P(A, B, C) &=P(A) P(B \mid A) P(C \mid B) \\[4pt] &=P(A) \frac{P(A \mid B) P(B)}{P(A)} P(C \mid B) \\[4pt] &=P(A \mid B) P(B) P(C \mid B) \end{align*} \nonumber \]

Мережа 3

Починаючи зараз із заяви для Мережі 2

\[\begin{align*} P(A, B, C) &=P(A \mid B) P(B) P(C \mid B) \\[4pt] &=P(A \mid B) P(B) \frac{P(B \mid C) P(C)}{P(B)} \\[4pt] &=P(A \mid B) P(B \mid C) P(C)\end{align*} \nonumber \]

Всі заміни засновані на правилі Байєса.

Існування класів еквівалентності свідчить про те, що причинність не може бути визначена випадковими спостереженнями. Контрольоване дослідження - яке тримає деякі змінні постійними, змінюючи інші для визначення ефекту кожного з них - необхідне для визначення точного причинно-наслідкового зв'язку, або байєсової мережі, набору змінних.

Теорема Байєса

Теорема Байєса, розроблена преподобним Томасом Байєсом, математиком і богословом 18 століття, вона виражається як:

\[P(H \mid E, c)=\frac{P(H \mid c) \cdot P(E \mid H, c)}{P(E \mid c)} \nonumber \]

де ми можемо оновити нашу віру в гіпотезу,\(H\) враховуючи додаткові\(E\) докази та довідкову інформацію\(c\). Лівий термін,\(P(H|E,c)\) відомий як «задня ймовірність», або ймовірність H після розгляду ефекту E заданого c Термін\(P(H|c)\) називається «попередня ймовірність»\(H\) даного c поодинці. Термін\(P(E|H,c)\) називається «ймовірність» і дає ймовірність доказів, припускаючи гіпотезу,\(H\) а довідкова інформація\(c\) є правдивою. Нарешті, останній термін\(P(E|c)\) називається «очікуваністю», або лише те, як очікувані докази даються\(c\). Він не залежить від\(H\) і може розглядатися як маргіналізуючий або масштабуючий фактор.

Його можна переписати як

\[P(E \mid c)=\sum_{i} P\left(E \mid H_{i}, c\right) \cdot P\left(H_{i} \mid c\right) \nonumber \]

де i позначає конкретну гіпотезу H _i, а підсумовування береться за сукупністю гіпотез, які є взаємовиключними і вичерпними (їх попередні ймовірності складають 1).

Важливо відзначити, що всі ці ймовірності є умовними. Вони вказують ступінь віри в якусь пропозицію або пропозиції, засновані на припущенні, що деякі інші пропозиції є істинними. Таким чином, теорія не має сенсу без попереднього визначення ймовірності цих попередніх пропозицій.

Байєс фактор

У випадках, коли ви не впевнені щодо причинно-наслідкових зв'язків між змінними та результатом при побудові моделі, ви можете використовувати коефіцієнт Байєса, щоб перевірити, яка модель краще описує ваші дані і, отже, визначити ступінь, в якій параметр впливає на результат ймовірності. Після використання теореми Байєса для побудови двох моделей з різними залежностями змінної залежності та оцінки ймовірності моделей на основі даних, можна обчислити коефіцієнт Байєса, використовуючи загальне рівняння нижче:

\[B F=\frac{p(\text {model} 1 \mid \text {data})}{p(\text {model} 2 \mid \text {data})}=\frac{\frac{p(\text {data} \mid \text {model} 1) p(\text {model} 1)}{p(\text {data})}}{\frac{p(\text {data} \mid \operatorname{model} 2) p(\operatorname{model} 2)}{p(\text {data})}}=\frac{p(\text {data} \mid \text {model} 1)}{p(\text {data} \mid \operatorname{model} 2)} \nonumber \]

Основна інтуїція полягає в тому, що попередня і задня інформація поєднуються в співвідношенні, яке дає докази на користь однієї моделі віршів іншого. Дві моделі в рівнянні коефіцієнта Байєса представляють два різних стани змінних, які впливають на дані. Наприклад, якщо досліджувані дані - це вимірювання температури, зняті з декількох датчиків, модель 1 може бути ймовірністю того, що всі датчики функціонують нормально, а модель 2 - ймовірність того, що всі датчики вийшли з ладу. Фактори Байєса дуже гнучкі, що дозволяє порівнювати кілька гіпотез одночасно.

Значення BF поблизу 1, вказують на те, що дві моделі майже однакові, а значення BF, далекі від 1, вказують на те, що ймовірність виникнення однієї моделі більша за іншу. Зокрема, якщо BF рівно> 1, модель 1 описує ваші дані краще, ніж модель 2. ЯКЩО BF дорівнює < 1, модель 2 описує дані краще, ніж модель 1. У нашому прикладі, якщо коефіцієнт Байєса 5 вказував би на те, що враховуючи дані про температуру, ймовірність нормального функціонування датчиків у п'ять разів перевищує ймовірність того, що датчики вийшли з ладу. Таблицю, що показує шкалу доказів за допомогою коефіцієнта Байєса, можна знайти нижче:

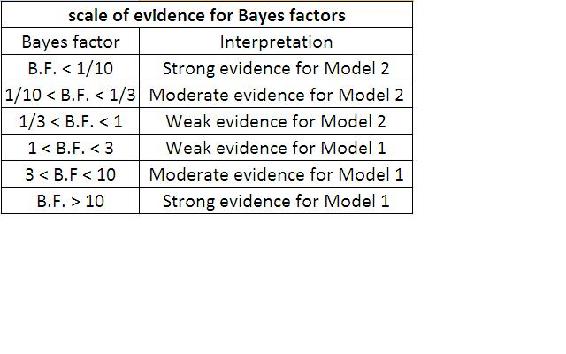
Хоча фактори Байєса досить інтуїтивно зрозумілі та прості для розуміння, як практична справа, їх часто досить важко обчислити. Існують альтернативи фактору Байєса для оцінки моделі, такі як Байєсовскій інформаційний критерій (BIC).

Формула для БИК така:

\[-2 \cdot \ln p(x \mid k) \approx \mathrm{BIC}=-2 \cdot \ln L+k \ln (n). \nonumber \]

• x = спостережувані дані; n = кількість точок даних в x, кількість спостережень, або еквівалентно розмір вибірки;
• k = кількість вільних параметрів, що підлягають оцінці. Якщо розрахункова модель є лінійною регресією, k - кількість регресорів, включаючи константу; p (x|k) = ймовірність спостережуваних даних за кількістю параметрів;
• L = максимальне значення функції правдоподібності для оцінюваної моделі.

Ця статистика також може бути використана для невкладених моделей. Для отримання додаткової інформації про Байєсівський інформаційний критерій, будь ласка, зверніться до:

Переваги та обмеження байєсівських мереж

Переваги Байєсівських мереж полягають у наступному:

• Байєсівські мережі візуально представляють всі зв'язки між змінними в системі з сполучними дугами.
• Легко розпізнати залежність і незалежність між різними вузлами.
• Байєсівські мережі можуть обробляти ситуації, коли набір даних є неповним, оскільки модель враховує залежності між усіма змінними.
• Байєсівські мережі можуть відображати сценарії, де неможливо виміряти всі змінні через системні обмеження (витрати, недостатньо датчиків тощо)
• Допоможіть моделювати галасливі системи.
• Може використовуватися для будь-якої моделі системи - від усіх відомих параметрів до невідомих параметрів.

Обмеження Байєсівських мереж такі:

• Всі гілки повинні бути розраховані для того, щоб обчислити ймовірність будь-якої однієї гілки.
• Якість результатів роботи мережі залежить від якості попередніх переконань або моделі. Змінна є лише частиною байєсівської мережі, якщо ви вважаєте, що система залежить від неї.
• Розрахунок мережі NP-Hard (недетермінований поліном-тимчасовий жорсткий), тому він дуже складний і, можливо, дорогий.
• Розрахунки та ймовірності, що використовують правило Байя та маргіналізацію, можуть стати складними і часто характеризуються тонкими формулюваннями, і потрібно подбати про їх належний розрахунок.

умовивід

Висновок визначається як процес отримання логічних висновків, заснованих на приміщеннях, відомих або прийнятих як істинні. Однією з сильних сторін байєсівських мереж є здатність до висновку, яка в даному випадку передбачає ймовірності неспостережуваних змінних в системі. Коли спостережувані змінні, як відомо, знаходяться в одному стані, ймовірності інших змінних матимуть різні значення, ніж загальний випадок. Візьмемо простий приклад системи, телебачення. Імовірність того, що телевізор увімкнено, поки люди вдома, набагато вища, ніж ймовірність того, що телебачення увімкнено, коли нікого немає вдома. Якщо відомий поточний стан телебачення, ймовірність того, що люди опиниться вдома, можна обчислити на основі цієї інформації. Це важко зробити вручну, але програмні програми, які використовують байєсівські мережі, містять висновок. Одна з таких програмних програм, Genie, впроваджується в Навчання та аналіз байєсівських мереж з Genie.

Маргіналізація

Маргіналізація параметра в системі може знадобитися в декількох випадках:

• Якщо дані по одному параметру (Р1) залежать від іншого, а дані для незалежного параметра не надаються.
• Якщо наведена таблиця ймовірностей, в якій P1 залежить від двох інших параметрів системи, але вас цікавить тільки вплив одного з параметрів на Р1.

Уявіть собі систему, в якій певний реагент (R) змішується в CSTR з каталізатором (C) і призводить до певного виходу продукту (Y). Три концентрації реагентів тестуються (A, B і C) з двома різними каталізаторами (1 і 2), щоб визначити, яка комбінація дасть найкращий вихід продукту. Оператор умовної ймовірності виглядає наступним чином:

\[P(R, C, Y)=P(R) P(C) P(Y \mid R, C) \nonumber \]

Таблиця ймовірностей встановлена таким чином, що ймовірність виходу певного продукту залежить від концентрації реагенту та типу каталізатора. Ви хочете передбачити ймовірність виходу певного продукту, враховуючи лише дані, які ви маєте для типу каталізатора. Концентрація реагенту повинна бути маргіналізована з P (Y|R, C), щоб визначити ймовірність виходу продукту, не знаючи концентрації реагенту. Таким чином, потрібно визначити P (Y|C). Рівняння маргіналізації показано нижче:

\[P(Y \mid C)=\sum_{i} P\left(Y \mid R_{i}, C\right) P\left(R_{i}\right) \nonumber \]

де підсумовування приймається за концентрації реагентів A, B і C.

Наступна таблиця описує ймовірність того, що зразок перевіряється з концентрацією реагентів A, B або C:

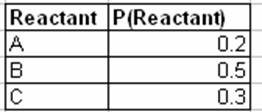
У наступній таблиці описана ймовірність спостереження виходу - High (H), Medium (M) або Low (L) - з урахуванням концентрації реагенту і типу каталізатора:

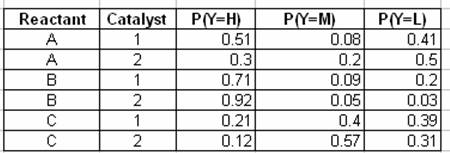
Останні дві таблиці показують розрахунок для маргіналізованих ймовірностей виходу заданого типу каталізатора за допомогою рівняння маргіналізації:

Динамічні байєсівські мережі

Статична байєсівська мережа працює лише зі змінними результатами з одного відрізка часу. В результаті статична байєсівська мережа не працює для аналізу розвивається системи, яка змінюється з плином часу. Нижче наведено приклад статичної байєсівської мережі для нафтового диководця:

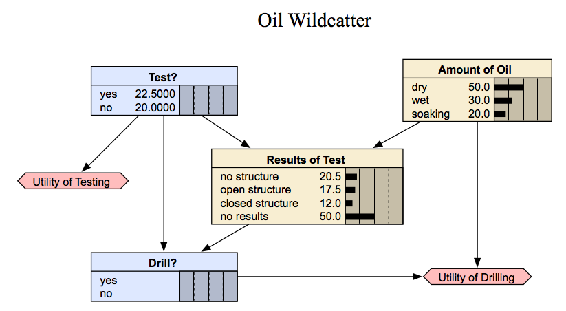
www.norsys.com/мережева бібліотека/index.htm

Нафта дикої природи повинен вирішити або бурити, чи ні. Однак йому потрібно визначити, чи є лунка суха, волога або мокнуча. Дикобійник міг приймати сейсмічні зондування, які допомагають визначити геологічну будову на ділянці. Зондування розкриє, чи не має місцевості нижче структури, що є поганою, або відкритою структурою, що нормально, або закритою структурою, що дійсно добре. Як бачите цей приклад не залежить від часу.

Динамічна Байєсівська мережа (DBN) є розширенням Байєсівської мережі. Він використовується для опису того, як змінні впливають один на одного з часом на основі моделі, отриманої з минулих даних. ДБН можна розглядати як модель ланцюга Маркова з багатьма станами або дискретне наближення за часом диференціального рівняння з тимчасовими кроками.

Прикладом ДБН, який показано нижче, є куля без тертя, що підстрибує між двома бар'єрами. При кожному кроці змінюється положення і швидкість.

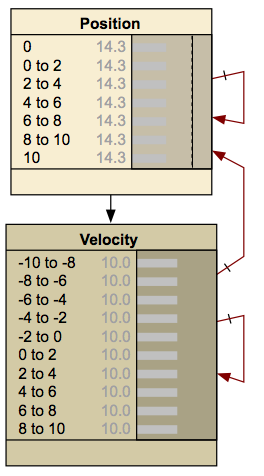
www.norsys.com/мережева бібліотека/index.htm

Важливе розмежування повинно проводитися між ланцюгами ДБН і Маркова. DBN показує, як змінні впливають один на одного з часом, тоді як ланцюжок Маркова показує, як розвивається стан всієї системи з часом. Таким чином, DBN проілюструє ймовірність зміни однієї змінної іншої, і як кожна з окремих змінних буде змінюватися з часом. Ланцюг Маркова розглядає стан системи, яка включає стан кожної окремої змінної, що становить систему, і показує ймовірності зміни станів системи з плином часу. Тому ланцюг Маркова включає всі змінні, присутні в системі, коли дивиться на те, як ця система розвивається з часом. Ланцюги Маркова можуть бути отримані з ДБН, але кожна мережа представляє різні значення і ймовірності.

Є кілька переваг у створення ДБН. Після того, як мережа була встановлена між часовими кроками, на основі цих даних може бути розроблена модель. Ця модель може бути використана для прогнозування майбутніх відповідей системи. Здатність прогнозувати майбутні відповіді також може бути використана для вивчення різних альтернатив для системи та визначення того, яка альтернатива дає бажані результати. DBN також забезпечують відповідне середовище для модельних прогнозних контролерів і можуть бути корисними при створенні контролера. Ще однією перевагою DBN є те, що їх можна використовувати для створення загальної мережі, яка не залежить від часу. Після того, як DBN було встановлено для різних кроків часу, мережу можна згорнути, щоб видалити компонент часу та показати загальні зв'язки між змінними.

DBN складається з взаємопов'язаних часових зрізів статичних байєсівських мереж. Вузли в певний час можуть впливати на вузли на майбутньому часовому відрізку, але вузли в подальшому не можуть впливати на вузли в попередньому часовому відрізку. Причинно-наслідкові зв'язки через часові зрізи називаються тимчасовими зв'язками, користь від цього полягає в тому, що вона дає ДБН однозначний напрямок причинності.

Для зручності обчислень передбачається, що змінні в DBN мають кінцеве число станів, які може мати змінна. Виходячи з цього, можуть бути побудовані таблиці умовних ймовірностей для вираження ймовірностей кожного дочірнього вузла, похідного від умов його батьківських вузлів.

Вузол C із зразка DAG вище матиме таблицю умовних ймовірностей із зазначенням умовного розподілу P (C|A, B). Оскільки A і B не мають батьків, тому для цього потрібні лише розподіли ймовірностей P (A) та P (B). Припускаючи, що всі змінні є двійковими, означає, що змінна A може приймати тільки A1 і A2, змінна B може приймати тільки B1 і B2, а змінна C може приймати тільки C1 і C2. Нижче наведено приклад таблиці умовних ймовірностей вузла C.

Умовні ймовірності між вузлами спостереження визначаються за допомогою сенсорного вузла. Цей вузол датчика дає умовний розподіл ймовірностей показань датчика з урахуванням фактичного стану системи. Вона втілює точність системи.

Характер ДБН зазвичай призводить до великої і складної мережі. Таким чином, щоб обчислити DBN, результат старий часовий зріз підсумовується в ймовірності, які використовуються для більш пізнього зрізу. Це забезпечує переміщення часових рамок і формує DBN. При створенні ДБН необхідно враховувати тимчасові відносини між зрізами. Нижче наведена діаграма реалізації DBN.

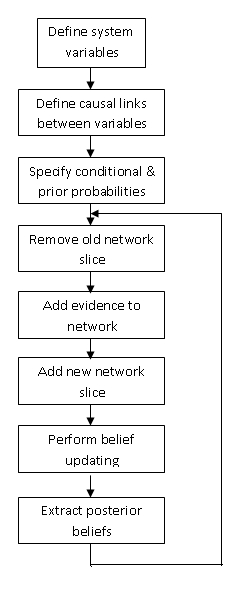
Графік нижче являє собою подання DBN. Він представляє змінні на двох різних кроках часу, t-1 і t. t-1, показаний зліва, є початковим розподілом змінних. Наступний часовий крок, t, залежить від часу кроку t-1. Важливо відзначити, що деякі з цих змінних можуть бути приховані.

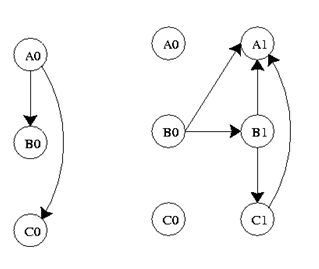
Де Ao, Bo, Co є початковими станами, а Ai, Bi, Ci - майбутні стани, де i = 1,2,3,..., n.

Розподіл ймовірності для цього ДБН в момент t дорівнює...

\[P\left(Z_{t} \mid Z_{t-1}\right)=\prod_{i=1}^{N} P\left(Z_{t}^{i} \mid \pi\left(Z_{t}^{i}\right)\right) \nonumber \]

Якщо процес триває протягом більшої кількості часових кроків, графік прийме форму нижче.

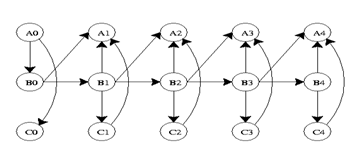
Його спільний розподіл ймовірностей буде...

\[P\left(Z_{1: T}\right)=\prod_{t=1}^{T} \prod_{i=1}^{N} P\left(Z_{t}^{i} \mid \pi\left(Z_{t}^{i}\right)\right) \nonumber \]

DBN корисні в промисловості, оскільки вони можуть моделювати процеси, де інформація є неповною або є невизначеність. Обмеження DBN полягають у тому, що вони не завжди точно прогнозують результати, і вони можуть мати тривалий обчислювальний час.

Наведені вище ілюстрації - це всі приклади «розгорнутих» мереж. Розгорнута динамічна байєсова мережа показує, як кожна змінна на одному кроці часу впливає на змінні на наступному етапі часу. Корисним способом думати про розгорнуті мережі є візуальні зображення числових розв'язків диференціальних рівнянь. Якщо ви знаєте стани змінних в один момент часу, і ви знаєте, як змінні змінюються з часом, то ви можете передбачити, яким буде стан змінних в будь-який момент часу, подібно до використання методу Ейлера для вирішення диференціального рівняння. Динамічну байєсівську мережу також можна представити у вигляді «прокатної» мережі. Згорнута мережа, на відміну від розгорнутої мережі, показує вплив кожної змінної одна на одну змінну на одній діаграмі. Наприклад, якщо у вас була розгорнута мережа виду:

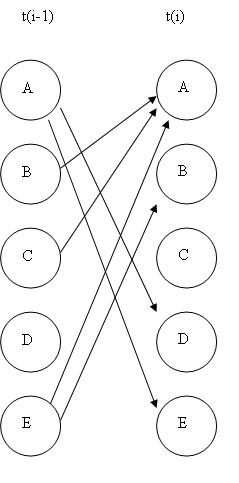
то ви можете представляти ту саму мережу в згорнутому вигляді, як:

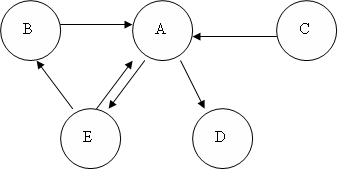
Якщо ви вивчите кожну мережу, ви побачите, що кожна з них надає точно таку ж інформацію про те, як змінні впливають один на одного.

Додатки

Байєсівські мережі використовуються, коли ймовірність того, що відбудеться одна подія, залежить від ймовірності того, що сталася попередня подія. Це дуже важливо в промисловості, оскільки в багатьох процесах змінні мають умовні відносини, тобто вони не незалежні один від одного. Байєсівські мережі використовуються для моделювання процесів у найрізноманітніших додатках. Деякі з них включають в себе...

1. Генні регуляторні мережі
2. білкова структура
3. діагностика хвороби
4. Класифікація документів
5. Обробка зображень
6. злиття даних
7. Системи підтримки прийняття рішень
8. Збір даних для дослідження глибокого космосу
9. Штучний інтелект
10. прогнозування погоди
11. На більш звичній основі, байєсівські мережі використовуються доброзичливим помічником офісу Microsoft для отримання кращих результатів пошуку. \
12. Інше використання байєсівських мереж виникає в кредитній галузі, де фізичній особі може бути присвоєно кредитний бал на основі віку, зарплати, кредитної історії тощо Це подається в байєсівську мережу, яка дозволяє компаніям кредитних карт вирішити, чи заслуговує кредитна оцінка особи сприятливе застосування.

Анотація: Загальний алгоритм розв'язку для незрозумілих

Враховуючи проблему мережі Байєса і поняття, з чого почати, просто розслабтеся і спробуйте виконати кроки, описані нижче.

Крок 1: Як виглядає моя мережа? Які вузли є батьками (і вони умовні чи безумовні), а які - діти? Як би я змоделював це як діаграму випадковості та який оператор умовної ймовірності визначає її?

Крок 2: Враховуючи моє підключення до мережі, як я можу скласти таблиці ймовірностей для кожного стану мого вузла (ів), що цікавлять? Для одного стовпця ймовірностей (батьківського вузла), чи сума стовпця дорівнює 1? Для масиву ймовірностей (дочірнього вузла) з декількома можливими станами, визначеними заданою комбінацією станів батьківського вузла, чи сума рядків дорівнює 1?

Крок 3: Враховуючи набір спостережуваних даних (зазвичай станів дочірнього вузла інтересу) та таблиць ймовірностей (ака таблиці істинності), яку проблему я вирішую?

• Імовірність спостереження конкретної конфігурації даних, порядок неважливий

Рішення: Застосуйте багатономіальний розподіл

• Імовірність спостереження конкретної конфігурації даних в тому конкретному порядку

Рішення: Обчисліть ймовірність кожного окремого спостереження, а потім візьміть добуток цих

• Імовірність спостереження даних у дочірньому вузлі, визначеному 2 (або n) батьками, заданою лише 1 (або n-1) батьківських вузлів

Рішення: Застосуйте маргіналізацію для усунення іншого батьківського вузла

• Імовірність того, що батьківський вузол є певним станом даних у вигляді спостережуваних станів дочірнього вузла

Рішення: Застосуйте
розв'язання теореми Байєса для коефіцієнта Байєса, щоб видалити невизначені терміни знаменника, породжені застосуванням теореми Байєса, та порівняти цікавить стан батьківського вузла з базовим випадком, отримуючи більш значущу точку даних

Крок 4: Чи вирішив я проблему? Або є інший рівень складності? Чи є проблема поєднанням варіацій проблеми, перелічених у кроці 3?

• Якщо проблема вирішена, зателефонуйте їй на день і йдіть, зробіть перерву на пахлаву
• Якщо проблема не вирішена, поверніться до кроку 3

Графічно:

Приклад\(\PageIndex{1}\)

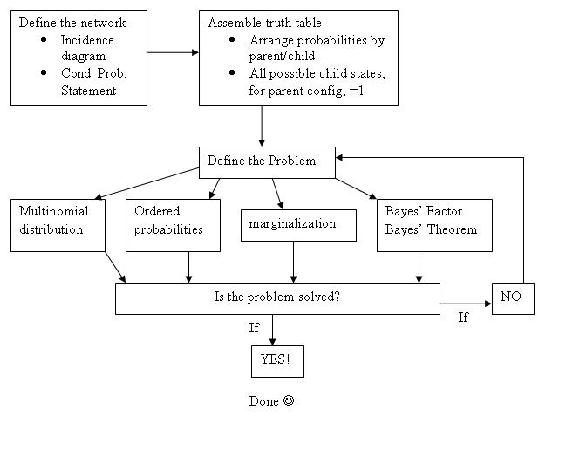
Багатофункціональну сигналізацію на заводі можна спрацьовувати двома способами. Сигналізація спрацьовує, якщо температура реактора занадто висока або тиск у резервуарі для зберігання занадто високий. Температура реактора може бути занадто високою через низький потік охолоджуючої води (ймовірність 1%), або через невідому побічну реакцію (ймовірність 5%). Тиск у резервуарі для зберігання може бути занадто високим через засмічення у вихідному трубопроводі (ймовірність 2%). Якщо витрата охолоджуючої води низький і є побічна реакція, то існує 99% ймовірність того, що відбудеться висока температура. Якщо потік охолоджуючої води нормальний і немає побічної реакції, існує лише 3% ймовірність виникнення високої температури. Якщо є засмічення труби, завжди буде виникати високий тиск. Якщо немає засмічення труб, високий тиск буде відбуватися тільки в 2% випадків.

Створіть DAG для наведеної вище ситуації та налаштуйте таблиці ймовірностей, необхідні для моделювання цієї системи. Всі значення, необхідні для заповнення цих таблиць, не наведені, тому заповніть те, що можливо, а потім вкажіть, які подальші значення потрібно знайти.

Рішення

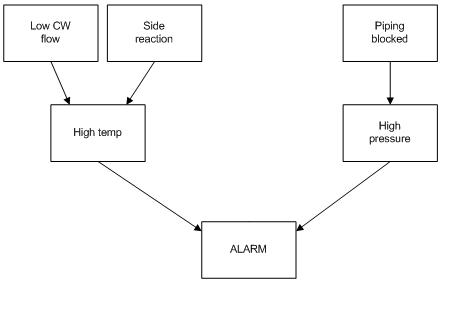
Наступні таблиці ймовірностей описують систему, де CFL = Потік холодної води низький, SR = Бічна реакція присутня, PB = Труба заблокована, HT = Висока температура, HP = Високий тиск, A = Сигналізація. T означає true, або подія відбулася. F розшифровується як false, або подія не відбулася. Пустий пробіл у таблиці вказує на область, де потрібна додаткова інформація.

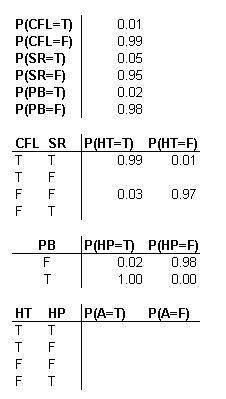
Перевага використання DAG стає очевидною. Наприклад, ви можете бачити, що існує лише 3% ймовірність того, що існує ситуація з високою температурою, враховуючи, що потік холодної води не низький і що немає бічної реакції.Однак, як тільки холодна вода стає низькою, у вас є принаймні 94% шансів на тривогу високої температури, незалежно від того, чи ні виникає побічна реакція. І навпаки, наявність побічної реакції тут лише створює 90% шанс тригера тривоги. З наведених вище розрахунків ймовірності можна оцінити відносне домінування причинно-наслідкових тригерів. Наприклад, тепер ви можете розумно припустити, що низька холодна вода є більш серйозною подією, ніж побічна реакція.

Приклад\(\PageIndex{2}\)

DAG, наведена нижче, зображує іншу модель, в якій тривога буде дзвонити при активації високої температури та/або витоку водопроводу теплоносія в реакторі.

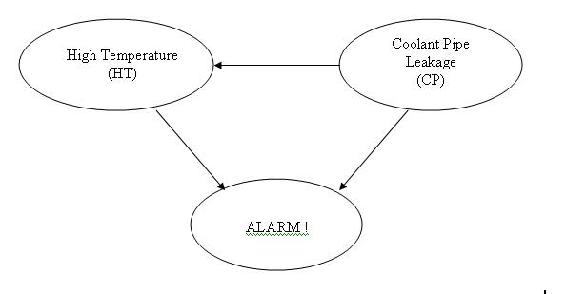
Наведена нижче таблиця показує таблицю істинності та ймовірності щодо різних ситуацій, які можуть виникнути в цій моделі.

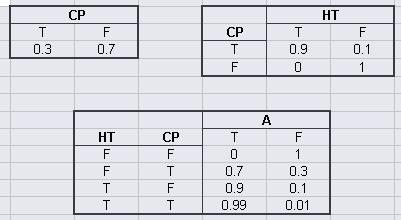
Функція ймовірності суглоба:

\[P(A,HT,CP) = P(A | HT,CP)P(HT | CP)P(CP) \nonumber \]

Відмінною особливістю використання Байєсівської мережі є те, що ймовірність будь-якої ситуації може бути розрахована. У цьому прикладі напишіть заяву, яка буде описувати ймовірність того, що температура в реакторі висока з урахуванням того, що звучить тривога.

Рішення

\[\mathrm{P}(C P=T \mid \Delta=T)=\frac{\mathrm{P}(A=T, C P=T)}{\mathrm{P}(A=1)} [= \dfrac{\sum_{HTC[T,P]}P(A-T, HT, CP-T)}{\sum_{HT, CPC[T,P]}P(A=T, HT, CP)} \nonumber \]

Приклад\(\PageIndex{3}\)

Певні ліки і травми можуть як викликати згустки крові. Згусток крові може призвести до інсульту, інфаркту, або він може просто розчинитися самостійно і не мати наслідків для здоров'я. Створіть DAG, який представляє цю ситуацію.

Рішення

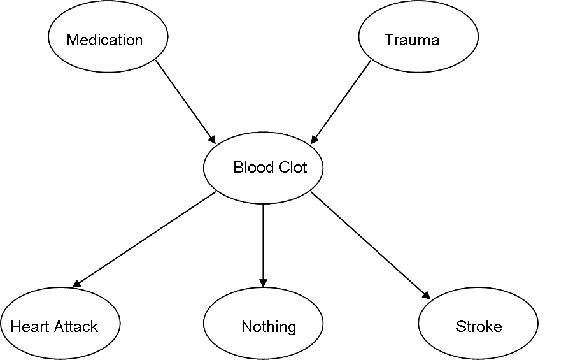
b. наведена наступна інформація про ймовірність, де M = ліки, T = травма, BC = згусток крові, HA = серцевий напад, N = нічого, а S = інсульт. T розшифровується як правда, або ця подія відбулася. F розшифровується як false, або ця подія не відбулося.

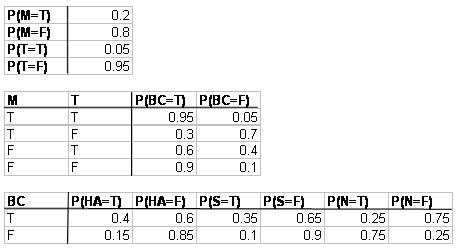
Яка ймовірність того, що у людини утвориться тромб в результаті як медикаментозного лікування, так і травми, а потім не матиме ніяких медичних наслідків?

Відповідь

\[\mathrm{P}(\mathrm{N}, \mathrm{BC}, \mathrm{M}, \mathrm{T})=\mathrm{P}(\mathrm{N} \mid \mathrm{BC}) \mathrm{P}(\mathrm{BC} \mid \mathrm{M}, \mathrm{T}) \mathrm{P}(\mathrm{M}) \mathrm{P}(\mathrm{T})=(0.25)(0.95)(0.2)(0.05)=0.2375 \% \nonumber \]

Приклад\(\PageIndex{4}\)

Припустимо, вам дали наступні дані.

Каталізатор	p (каталізатор)
A	0,40
Б	0,60

Температура	Каталізатор	P (Вихід = Н)	P (Вихід = М)	P (Вихід = L)
Ч	A	0,51	0,08	0,41
Ч	Б	0,30	0,20	0,50
М	A	0,71	0,09	0,20
М	Б	0,92	0,05	0,03
Л	A	0,21	0,40	0,39
Л	Б	0,12	0,57	0,31

Як би ви використали ці дані, щоб знайти p (yield|temp) для 9 спостережень з наступними описами?

# Часи спостерігаються	Температура	врожайність
4х	Ч	Ч
2х	М	Л
3х	Л	Ч

DAG цієї системи наведено нижче:

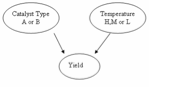
Рішення

Маргіналізація! Стан каталізатора можна маргіналізувати за допомогою наступного рівняння:

p (вихід | темп) =	∑	р (врожайність | темп, кіт i р) (кіт i)
	i = А, В

Дві таблиці вище можна об'єднати, щоб сформувати нову таблицю з маргіналізацією:

Температура	P (Вихід = Н)	P (Вихід = М)	P (Вихід = L)
Ч	0,51*0,4 + 0,3*0,6 = 0,384	0,08*0,4 + 0,2*0,6 = 0,152	0,41*0,4 +0,5*0,6 = 0,464
М	0,71* 0,4 + 0,92*0,6 = 0,836	0,09*0,4 + 0,05*0,6 = 0,066	0,20*0,4 + 0,03*0,6 = 0,098
Л	0,21*0,4 + 0,12*0,6 = 0,156	0,40*0,4 + 0,57*0,6 = 0,502	0,39*0,4 + 0,31*0,6 = 0,342

\[p(\text {yield} \mid \text {temp})=\frac{9 !}{4 ! 2 ! 3 !} *\left(0.384^{4} * 0.098^{2} * 0.156^{3}\right)=0.0009989 \nonumber \]

Приклад\(\PageIndex{5}\)

Дуже корисним використанням байєсівських мереж є визначення того, чи є датчик, швидше за все, працює або зламаний на основі поточних показань за допомогою байєсового фактора, розглянутого раніше. Припустимо, у вашому процесі є великий чан з великим турбулентним потоком, що ускладнює точне вимірювання рівня в чані. Щоб допомогти вам використовувати два різних датчика рівня, розташовані навколо резервуара, які свідчать, чи є рівень високим, нормальним чи низьким. При першому налаштуванні сенсорної системи ви отримали наступні ймовірності, що описують шум датчика, що працює нормально.

Рівень бака (L)	p (S = високий)	p (S = нормальний)	p (S = низький)
Вище діапазону робочих рівнів	0,80	0,15	0,05
В межах діапазону робочих рівнів	0,15	0,75	0,10
Нижче діапазону робочих рівнів	0,10	0,20	0,70

Коли датчик виходить з ладу, існує однакова ймовірність того, що датчик повідомляє про високий, нормальний або низький незалежно від фактичного стану бака. Таблиця умовних ймовірностей для датчика несправності тоді виглядає так:

Рівень бака (L)	p (S = високий)	p (S = нормальний)	p (S = низький)
Вище діапазону робочих рівнів	0,33	0,33	0,33
В межах діапазону робочих рівнів	0,33	0,33	0,33
Нижче діапазону робочих рівнів	0,33	0,33	0,33

З попередніх даних ви визначили, що коли процес діє нормально, як ви вважаєте, що зараз, резервуар буде працювати вище діапазону рівня 10% часу, в діапазоні рівнів 85% часу, і нижче діапазону рівня 5% часу. Дивлячись на останні 10 спостережень (показані нижче), ви підозрюєте, що датчик 1 може бути зламаний. Використовуйте байєсовські фактори для визначення ймовірності поломки датчика 1 порівняно з робочими обома датчиками.

Сенсор 1	Датчик 2
Високі	Нормальний
Нормальний	Нормальний
Нормальний	Нормальний
Високі	Високі
Низький	Нормальний
Низький	Нормальний
Низький	Низький
Високі	Нормальний
Високі	Високі
Нормальний	Нормальний

З визначення байєсового фактора отримаємо.

Для цього набору ми будемо використовувати ймовірність того, що ми отримаємо дані, наведені на основі моделі.

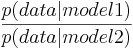
Якщо розглядати модель 1 як датчики, що працюють, так і датчик 2 моделі 2 зламані, ми можемо знайти BF для цього досить легко.

p (дані | модель 1) = p (дані s1 | модель 1) * p (дані s2 | модель 1)

Для обох датчиків працюють належним чином:

Імовірність того, що датчик дає кожне показання, повинна бути розрахована спочатку, що можна знайти, підсумовуючи ймовірність того, що бак буде на кожному рівні, і помноживши на ймовірність отримання конкретного показання на цьому рівні для кожного рівня.

p (s1 = високий | модель 1) = [(.10) * (.80) + (.85) * (0,15) + (0,05) * (.10) = 0,2125

р (s1 = нормальний | модель 1) = [(.10) * (.15) + (.85) * (.75) + (.05) * (.20) = 0,6625

p (s1 = низький | модель 1) = [(.10) * (0,05) + (.85) * (.10) + (0,05) * (.70) = 0,125

Імовірність отримання показань датчика 1 (за умови нормальної роботи)

p (s 1 дані | модель 1) = (.2125) ⁴ * (.6625) ³ * (.125) ³ = 5,450 * 10 ^{− 6}

Імовірність отримання кожного показання для датчика 2 буде однаковою, оскільки він також працює нормально.

p (s 2 дані | модель 1) = (.2125) ² * (.6625) ⁷ * (.125) ¹ = 3,162 * 10 ^{− 4}

p (дані | модель 1) = (5,450 * 10 ^{− 6}) * (3,12* 10 ^{− 4}) = 1,723* 10 ^{− 9}

Для зламаного датчика 1:

Імовірність отримання кожного показання зараз для датчика буде 0,33.

p (s 1 дані | модель 2) = (0,33) ⁴ * (0,33) ³ * (0,33) ³ = 1,532* 10 ^{− 5}

Імовірність отримання показань для датчика 2 буде такою ж, як у моделі 1, так як обидві моделі припускають, що датчик 2 працює нормально.

p (дані | модель 2) = (1,532* 10 ^{− 5}) * (3,12* 10 ^{− 4}) = 4,844* 10 ^{− 9}

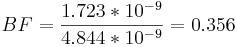
Коефіцієнт BF між 1/3 і 1 означає, що є слабкі докази того, що модель 2 є правильною.

Правда чи брехня?

1. Чи є інша назва Байєсівської мережі «Віруючий» Мережа?

2. Вузли в байєсовій мережі можуть представляти будь-який вид змінної (прихована змінна, вимірюваний параметр, гіпотеза..) і не обмежуються випадковими величинами.

3. Байєсівська теорія мереж використовується в частині процесу моделювання штучного інтелекту.

Відповіді:

1. F

2. Т

3. Т

Посилання

1. Аксой, Селім. «Параметричні моделі Частина IV: Байєсівські мережі вірувань». Весна 2007 року. <www.cs.bilkent.edu.tr/~saksoy/courses/cs551/slides/cs551_parametric4.pdf>
2. Бен-Гал, Ірад. «БАЙЄСІВСЬКІ МЕРЕЖІ». Кафедра промислової інженерії. Тель-Авівський університет. < http://www.eng.tau.ac.il/~bengal/BN.pdf > http://www.dcs.qmw.ac.uk/~norman/BBNs/BBNs.htm
3. Чарняк, Євген (1991). «Байєсівські мережі без сліз», журнал AI, стор. 8.
4. Фрідман, Нір, Лініал, Міхал, Нахман, Іфтах, і Пеер, Дана. «Використання байєсівських мереж для аналізу даних виразів». ЖУРНАЛ ОБЧИСЛЮВАЛЬНОЇ БІОЛОГІЇ, Том 7, # 3/4, 2000, Мері Енн Ліберт, Inc. с. 601—620 <www.sysbio.harvard.edu/csb/ramanathan_lab/iftach/papers/FLNP1Full.pdf>
5. Го, Хайпен. «Динамічні байєсівські мережі». Серпень 2002 року. <www.kddresearch.org/Groups/Probabilistic-Reasoning/258,1, Slide 1>
6. Ніл, Мартін, Фентон, Норман, і Кравець, Манеш. «Використання байєсівських мереж для моделювання очікуваних та несподіваних операційних втрат». Аналіз ризиків, том 25, № 4, 2005 < http://www.dcs.qmul.ac.uk/~norman/papers/oprisk.pdf >
7. Нідермайер, Даріл. «Вступ до байєсівських мереж та їх сучасних застосувань». 1 грудня 1998 року. < http://www.niedermayer.ca/papers/bayesian/bayes.html >
8. Сілі, Річ. «Байєсівські мережі зробили легко». Тенденції розвитку додатків. 4 грудня 2007 р. <www.adtmag.com/стаття. aspxid=10271 &сторінка=>.
9. http://en.Wikipedia.org/wiki/Bayesian_network

Дописувачі та атрибуція

• Автори: Сара Хеберт, Валері Лі, Метью Морабіто, Джеймі Полан