1.4: Криві напруження-деформації

Вступ

Криві напруження-деформації є надзвичайно важливою графічною мірою механічних властивостей матеріалу, і всі студенти механіки матеріалів стикаються з ними часто. Однак вони не позбавлені деяких тонкощів, особливо у випадку з пластичними матеріалами, які можуть піддаватися субстанціальним геометричним змінам під час випробувань. Цей модуль забезпечить вступне обговорення декількох моментів, необхідних для інтерпретації цих кривих, і при цьому також надасть попередній огляд декількох аспектів механічних властивостей матеріалу. Однак цей модуль не намагатиметься оглянути широкий спектр кривих напруження-деформації, що демонструються сучасними інженерними матеріалами (для цього можна проконсультуватися з атласом Боєра, який наведено в розділі «Посилання»). Кілька згаданих тут тем - особливо врожайність і руйнування - з'являться більш детально в наступних модулів.

«Інженерні» криві напруження-деформації

Мабуть, найважливішим випробуванням механічної реакції матеріалу є випробування на розтяг (випробування на напруження-деформацію, а також майже всі експериментальні процедури в механіці матеріалів, деталізовано організаціями, що встановлюють стандарти, зокрема Американським товариством випробувань та матеріалів (ASTM). Випробування металів на розрив призначається ASTM Test E8, пластмаси по ASTM D638, і композитні матеріали ASTM D3039.), в якому один кінець зразка стрижня або дроту затискається в навантажувальній рамі, а інший піддається контрольованому переміщенню$\delta$ (див. Рис. Передавач, з'єднаний послідовно зі зразком, забезпечує електронне зчитування навантаження,$P (\delta)$ відповідного зміщенню. Як варіант, сучасні сервокеровані випробувальні машини дозволяють використовувати навантаження, а не переміщення в якості керованої змінної, і в цьому випадку переміщення$\delta (P)$ буде контролюватися як функція навантаження.

Інженерні заходи напруги і деформації, позначені в цьому модулі як σ і εe відповідно, визначаються з виміряного навантаження і прогину з використанням вихідної площі перерізу$A_0$ і довжини зразка$L_0$ як

$$\sigma_e = \dfrac{P}{A_0}, \epsilon_e = \dfrac{\delta}{L_0}$$

Коли напруга σ наноситься на деформацію$\epsilon_e$, виходить інженерна крива напруження-деформації, така як показано на малюнку 2.

Малюнок 1: Випробування на натяг.

Малюнок 2: Низькодеформована область інженерної кривої напруження-деформації для відпаленої полікристалічної міді; ця крива характерна для багатьох пластичних металів.

У ранній (низькодеформаційній) частині кривої багато матеріалів підкоряються закону Гука до розумного наближення, так що напруга пропорційна деформації, а константа пропорційності є модулем пружності або модулем Юнга, що позначається$E$:

$$\sigma_e = E_{\epsilon_e}$$

Оскільки деформація збільшується, багато матеріалів врешті-решт відхиляються від цієї лінійної пропорційності, точку відправлення називають пропорційною межею. Ця нелінійність, як правило, як- асоціюється з індукованим стресом «пластичним» потоком у зразку. Тут матеріал переживає перестановку своєї внутрішньої молекулярної або мікроскопічної структури, при якій атоми переміщуються в нові положення рівноваги. Ця пластичність вимагає механізму молекулярної mo- здатності, яка в кристалічних матеріалах може виникнути внаслідок руху дислокації (розглянуто далі в більш пізньому модулі). Матеріали, які не мають такої рухливості, наприклад, через внутрішні мікроструктури, які блокують рух дислокації, зазвичай крихкі, а не пластичні. Крива напруження-деформації для крихких матеріалів, як правило, лінійна в повному діапазоні деформації, врешті-решт закінчується руйнуванням без помітного пластичного потоку.

Зверніть увагу на малюнку 2, що напруга, необхідна для збільшення деформації за межі пропорційної межі в пластичному матеріалі, продовжує підніматися за пропорційну межу; матеріал вимагає постійно зростаючого напруження для продовження напруження, механізм, який називається деформаційним зміцненням.

Ці мікроструктурні перебудови, пов'язані з пластичним потоком, зазвичай не змінюються, коли навантаження знімається, тому пропорційна межа часто така ж, як або принаймні близька до межі пружності матеріалів. Еластичність - це властивість повного і негайного відновлення від нав'язаного зміщення при звільненні вантажу, а межа пружності - величина напруги, при якій матеріал відчуває постійну залишкову деформацію, яка не втрачається при розвантаженні. Залишкова деформація, індукована заданою напругою, може бути визначена шляхом проведення лінії розвантаження від найвищої точки, досягнутої на кривій se - ee при цьому напруженні назад до осі деформації, проведеної з нахилом, рівним початковій пружної лінії навантаження. Це робиться тому, що матеріал розвантажується пружно, не маючи сили, що рухає молекулярну структуру назад у вихідне положення.

Тісно пов'язаним терміном є межа плинності, що позначається$\sigma_Y$ в цих модулів; це напруга, необхідна для індукування пластичної деформації в зразку. Оскільки часто важко точно визначити напругу, при якій починається пластична деформація, напруга плинності часто вважається напругою, необхідною для індукування певної кількості постійної деформації, як правило, 0,2%. Конструкція, яка використовується для пошуку цього «зміщення напруги текучості», показана на малюнку 2, на якому лінія нахилу$E$ проводиться від осі деформації при$\epsilon_e$ = 0,2%; це лінія розвантаження, яка призведе до зазначеної постійної деформації. Напруга в точці перетину з$\sigma_e - \epsilon_e$ кривою - це зміщення напруженості плинності.

На малюнку 3 показана інженерна крива напруження-деформації для міді зі збільшеною шкалою, тепер показує деформації від нуля до руйнування зразка. Тут виявляється, що швидкість деформаційного зміцнення (Швидкість деформаційного зміцнення - це нахил кривої напруження-деформація, яку також називають дотичним модулем.) зменшується до точки, позначеної UTS, для граничної міцності на розрив (позначається σf у цих модулів). Поза цією точкою матеріал, здається, розм'якшується, так що кожне збільшення додаткової деформації вимагає меншого напруження.

Малюнок 3: Повна інженерна крива напруження-деформації для відпаленої полікристалічної міді.

Очевидна зміна від деформаційного зміцнення до пом'якшення деформації є артефактом процедури побудови, однак, як і максимум, що спостерігається в кривій на UTS. Крім межі текучості, молекулярний потік викликає значне зменшення площі поперечного перерізу зразка$A$, тому справжнє напруження, яке$\sigma_t = P/A$ насправді несе матеріал, більше, ніж інженерне напруження, обчислене з початкової площі поперечного перерізу ($\sigma_e = P/A_0$). Навантаження повинно дорівнювати справжньому напруженню, що перевищує фактичну площу ($P = \sigma_t A$), і до тих пір, поки деформаційне зміцнення може зростати$\sigma_t$ достатньо, щоб компенсувати зменшену площу$A$, навантаження і, отже, інженерне напруження будуть продовжувати зростати зі збільшенням деформації. З часом, однак, зменшення площі за рахунок потоку стає більше, ніж збільшення справжнього напруження внаслідок деформаційного затвердіння, і навантаження починає падати. Це геометричний ефект, і якби було побудовано справжнє напруження, а не інженерне напруження, максимум не буде спостерігатися в кривій.

На УТС диференціал навантаження$P$ дорівнює нулю, що дає аналітичну залежність між істинним напруженням і площею при шийці:

$$P = \sigma_t A \to dP = 0 = \sigma_t dA + A d \sigma_t \to -\dfrac{dA}{A} = \dfrac{d\sigma_t}{\sigma_t}$$

Останній вираз стверджує, що навантаження і, отже, інженерне напруження досягне максимуму як функція деформації, коли дробове зменшення площі стане рівним дробовому збільшенню справжнього напруження.

Незважаючи на те, що UTS є, мабуть, властивістю матеріалів, які найчастіше повідомляються при випробуваннях на розтяг, це не є прямим заходом матеріалу через вплив геометрії, як обговорювалося вище, і його слід використовувати з обережністю. Межа плинності σ Y зазвичай віддається перевазі UTS при проектуванні з пластичними металами, хоча UTS є дійсним критерієм конструкції для крихких матеріалів, які не демонструють цих скорочень, викликаних потоком площі поперечного перерізу.

Справжній стрес не зовсім рівномірний у всьому зразку, і завжди буде якесь місце - можливо, нік або якийсь інший дефект на поверхні - де локальне напруження максимальне. Після досягнення максимуму в інженерній кривій локалізований потік на цій ділянці не може бути компенсований подальшим деформаційним зміцненням, тому площа там зменшується далі. Це ще більше збільшує місцевий стрес, що прискорює перебіг далі. Цей локалізований і зростаючий потік незабаром призводить до «шийки» в довжині зразка, як показано на малюнку 4.

Малюнок 4: Шийка в розтягнутому зразку.

Поки не утворюється шийка, деформація по суті рівномірна по всьому зразку, але після шийки вся наступна деформація відбувається в шиї. Шийка стає все менше і менше, місцевий справжній стрес весь час збільшується, поки зразок не вийде з ладу. Це буде режим відмови для більшості пластичних металів. Коли шийка стискається, неоднорідна геометрія змінює одновісний напружений стан до складного, що включає компоненти зсуву, а також нормальні напруги. Зразок часто виходить з ладу остаточно з геометрією «чашки і конуса», як показано на малюнку 5, в якій зовнішні області виходять з ладу в зсуві, а внутрішня частина - в напрузі. Коли зразок руйнується, інженерна деформація при розриві$\epsilon_f$ - позначається - буде включати деформацію в області шиї та нешийної області разом. Оскільки справжня деформація в шийці більше, ніж у нешийному матеріалі, значення$\epsilon_f$ буде залежати від частки довжини калібру, яка має шию. Тому$\epsilon_f$ є функцією геометрії зразка, а також матеріалу, і, таким чином, є лише грубою мірою пластичності матеріалу.

Малюнок 5: Руйнування чашки і конуса в пластичному металі.

На малюнку 6 показана інженерна крива напруження-деформації для напівкристалічного термопласта. Відповідь цього матеріалу подібна до реакції міді, показаної на малюнку 3, оскільки вона показує пропорційну межу, за якою слідує максимум у кривій, на якій відбувається шийка. (Зазвичай цей максимум називають напругою плинності у пластмасах, хоча потік пластику фактично почався при більш ранніх деформаціях.)

Малюнок 6: Крива напруження-деформація для поліамідного (нейлонового) термопласта.

Полімер, однак, різко відрізняється від міді тим, що шийка не продовжує скорочуватися, поки зразок не вийде з ладу. Швидше за все, матеріал у шиї розтягується лише до «природного співвідношення витягування», яке є функцією температури та обробки зразків, за межами якої матеріал у шиї перестає розтягуватися, а новий матеріал на шиї плечі опускається вниз. Потім шия поширюється, поки вона не охоплює повну довжину зразка, процес, який називається малюванням. Цей процес можна спостерігати без необхідності випробувальної машини, розтягуючи поліетиленовий «шестипакетний тримач», як видно на малюнку 7.

Не всі полімери здатні витримати цей процес малювання. Як буде розглянуто в наступному розділі, це відбувається, коли процес шийки виробляє посилену мікроструктуру, розривне навантаження якої більше, ніж необхідне для спричинення шийки в нетранформованому матеріалі безпосередньо поза шиєю.

Малюнок 7: Шийка і малювання в 6-пакетному тримачі.

«Справжні» криві напруження-деформації

Як обговорювалося в попередньому розділі, інженерну криву напруження-деформації слід інтерпретувати з обережністю за межі пружності, оскільки розміри зразка відчувають суттєву зміну від своїх початкових значень. Використання справжнього напруження,$\sigma_t = P/A$ а не інженерного напруження$\sigma_e = P/A_0$ може дати більш прямий вимір реакції матеріалу в діапазоні потоку пластику. Міра деформації, яка часто використовується в поєднанні з істинним напруженням, приймає приріст деформації як поступове збільшення зміщення dL, поділене на поточну довжину$L$:

$$d \epsilon_t = \dfrac{dL}{l} \to \epsilon_t = \int_{l_0}^{L} \dfrac{1}{L} dL = \ln \dfrac{L}{L_0}$$

Це називається «істинним» або «логарифмічним» штамом.

Під час виходу і режиму пластичного потоку після виходу матеріал тече з незначною зміною обсягу; збільшення довжини компенсується зменшенням площі поперечного перерізу. Перед шийкою, коли деформація все ще рівномірна по довжині зразка, це обмеження обсягу може бути записано:

$$dV = 0 \to AL = A_0 L_0 \to \dfrac{L}{L_0} =\dfrac{A}{A_0}$$

Співвідношення$L/L_0$ - коефіцієнт розширення, що позначається як$\lambda$. Використовуючи ці відносини, легко виробити зв'язки між істинними і інженерними заходами розтягуючого напруження і деформації (див. Вправа$\PageIndex{2}$):

$$\sigma_1 = \sigma_e (1 + \epsilon_e) = \sigma_e \lambda, \epsilon_t = \ln (1 + \epsilon_e) =\ln \lambda$$

Ці рівняння можуть бути використані для отримання істинної кривої напруження-деформації від інженерної кривої, аж до деформації, при якій починається шийка. Рисунок 8 - це репліт малюнка 3, з істинною кривою напруження-деформації, обчисленої цією процедурою, доданою для порівняння.

Крім шийки, деформація неоднорідна в довжині калібру, і для обчислення справжньої кривої напруження-деформації для більших інженерних деформацій не було б значущим. Однак повну справжню криву напруження-деформації можна було б намалювати, якщо область шиї контролювалася протягом усього випробування на розтяг, оскільки для логарифмічної деформації ми маємо

$$\dfrac{L}{L_0} = \dfrac{A}{A_0} \to \epsilon_t = \ln \dfrac{L}{L_0} = \ln \dfrac{A}{A_0}$$

Ковкі метали часто мають справжні напружено-деформовані відносини, які можна описати простим силовим зв'язком виду:

Малюнок 8: Порівняння інженерних та істинних кривих напруження-деформації для міді. Стрілкою вказується положення на «істинній» кривій УТС на інженерній кривій.

$$\sigma_t = A\epsilon_t^n \to \log \sigma_t = \log A + n \log \epsilon_t$$

Рисунок 9 - це графік журналу справжніх даних про напруження-деформацію (Тут використано відсоток деформації$\epsilon_t$; це дає те саме значення для,$n$ але інше,$A$ ніж якщо були використані повні, а не процентні значення.) для міді на рис. 8, що демонструє це відношення. Тут параметр$n = 0.474$ називається параметром деформаційного зміцнення, корисним як міра опору шийці. Ковкі метали при кімнатній температурі зазвичай виявляють значення$n$ від 0,02 до 0,5.

Малюнок 9: Представлення закону потужності пластичного відношення напруження-деформація для міді.

Графічний метод, відомий як «конструкція Consid`ere», використовує форму справжньої кривої напруження-деформації для кількісної оцінки відмінностей у шийці та малюванні від матеріалу до матеріалу. Цей метод повторює криву напруження-деформації при розтягуванні з істинним напруженням$\sigma_t$ як ординатним і коефіцієнтом розтягування$\lambda = L/L_0$ як абсциси. З Рівняння 1.4.6 інженерне напруження,$\sigma_e$ відповідне будь-якому значенню справжнього напруження,$\sigma_t$ є нахилом січної лінії, проведеної від$\lambda = 0$ початку (, не$\lambda = 1$) для перетину$\sigma_t - \lambda$ кривої в$\sigma_t$.

Малюнок 10: Розглянемо конструкцію. (а) Справжня крива напруження-деформації без дотичних - відсутність шийки або малювання. (б) Одна дотична - шийка, але не малюнок. (в) Дві дотичні - горловина і витяжка.

Серед багатьох можливих форм можуть припустити справжні криві напруження-деформації, розглянемо увігнуті вгору, увігнуті вниз та сигмоїдальні форми, показані на малюнку 10. Вони відрізняються кількістю дотичних точок, які можна знайти для січної лінії, і дають такі характеристики плинності:

(а) Немає дотичних: Тут крива завжди увігнута вгору, як у частині (а) малюнка 10, тому нахил січної лінії безперервно піднімається. Тому інженерне напруження також підвищується, не показуючи падіння врожайності. Зрештою руйнування переступається, тому справжня крива напруження-деформації цієї форми ідентифікує матеріал, який руйнується до того, як він дає.

(b) Одна дотична: Крива увігнута вниз, як у частині (b) малюнка 10, тому січна лінія досягає точки дотичної в$\lambda = \lambda_Y$. Нахил січної лінії, а значить і інженерне напруження в тому числі, починає падати саме в цій точці. Це тоді напруга плинності σ Y розглядається як максимум в напрузі на звичайній кривій напруження-деформації, і$\lambda_Y$ є коефіцієнтом розширення при врожайності. Процес врожайності починається в деякому додатковому місці в довжині зразка, і триває в цьому місці, а не ініціюється в іншому місці, оскільки модуль секантності був зменшений на першому місці. Зараз зразок тече в одному місці зі зменшенням опору, що призводить в кінцевому підсумку до відмови. Ковкі метали, такі як алюміній, виходять з ладу таким чином, демонструючи помітне зменшення площі поперечного перерізу в положенні текучості та можливого руйнування.

(c) Дві тангенси: Для сигмоїдальних кривих напруження-деформації, як у частині (c) малюнка 10, інженерне напруження починає падати при коефіцієнті розширення$\lambda_Y$, але потім знову піднімається на$\lambda_d$. Як і в попередньому однодотичному випадку, матеріал починає поступатися в одному положенні$\lambda = \lambda_Y$, коли, виробляючи шийку, яка в свою чергу передбачає нерівномірний розподіл деформації по довжині датчика. Матеріал при розташуванні горловини потім розтягується до$\lambda_d$, після чого інженерне напруження там доведеться підніматися, щоб розтягнути його далі. Але ця напруга більше, ніж потрібно для розтягування матеріалу по краю горловини від$\lambda_Y$ до$\lambda_d$, тому матеріал вже в шиї перестає розтягуватися і шия поширюється назовні від початкового місця виходу. Тільки матеріал всередині плечей шиї розтягується під час розповсюдження, при цьому матеріал всередині області шиї вниз тримається постійною в$\lambda_d$, «природне співвідношення малювання» матеріалу, і матеріал зовні тримається на$\lambda_Y$. Коли весь матеріал був втягнутий в область шиї, напруга починає рівномірно підніматися в зразку, поки врешті-решт не відбудеться руйнування.

Збільшення швидкості деформаційного зміцнення, необхідного для підтримки процесу витягування в напівкристалічних полімерах, виникає внаслідок різкого перетворення в мікроструктурі матеріалу. Ці матеріали спочатку «сферулітичні», що містять плоскі пластинчасті кристалічні пластини товщиною, можливо, 10 нм, розташовані радіально назовні в сферичній області. Зі збільшенням індукованої деформації ці сферуліти спочатку деформуються в напрямку напруження. У міру подальшого збільшення деформації сферуліти розбиваються, а пластинчасті фрагменти переставляються з домінуючою осьовою молекулярною орієнтацією, щоб стати тим, що відомо як фібрилярна мікроструктура. З міцними ковалентними зв'язками, які зараз переважають у несучому напрямку, матеріал демонструє помітно більшу міцність та жорсткість - можливо, на порядок - ніж у вихідному матеріалі. Ця структура вимагає набагато більшої швидкості деформаційного зміцнення для збільшення деформації, що спричиняє підйом і другий тангенс у істинній кривій напруження-деформації.

Енергія деформації

Площа під$\sigma_e - \epsilon_e$ кривою до заданого значення деформації - це загальна механічна енергія на одиницю об'єму, споживаного матеріалом при напруженні його до цієї величини. Це легко показано наступним чином:

$$U^* = \dfrac{1}{V} \int P\ dL = \int_0^L \dfrac{P}{A_0} \dfrac{dL}{L_0} = \int_{0}^{\epsilon} \sigma d\epsilon$$

За відсутності молекулярного ковзання та інших механізмів розсіювання енергії ця механічна енергія зберігається оборотно всередині матеріалу як енергія деформації. Коли напруження досить низькі, щоб матеріал залишався в пружному діапазоні, енергія деформації - це всього лише трикутна область на малюнку 11:

Малюнок 11: Енергія деформації = площа під кривою напруження-деформація.

Зверніть увагу, що енергія деформації збільшується квадратично з напругою або деформацією; тобто, що, коли деформація збільшує енергію, накопичену при заданому збільшенні додаткової деформації, зростає у міру зростання квадрата деформації. Це має важливі наслідки, одним із прикладів є те, що лук для стрільби з лука не може бути просто вигнутим шматком дерева, щоб добре працювати. Справжній лук спочатку прямий, потім зігнутий, коли його нанизують; це зберігає в ньому значну енергію деформації. Коли він згинається далі на малюванні стріли назад, енергія, доступна для кидання стріли, дуже набагато більше, ніж якби лук був просто вирізаний у вигнутій формі, фактично не згинаючи його.

На малюнку 12 схематично показано кількість енергії деформації, доступної для двох рівних кроків деформації$\Delta_{\epsilon}$, застосованих на різних рівнях існуючої деформації.

Малюнок 12: Енергія, пов'язана з приростами деформації

Таблиця 1: Енергопоглинання різних матеріалів.

Матеріал	Максимальний штам,%	Максимальне напруження, МПа	Модуль міцності,$MJ/m^3$	Щільність$kg/m^3$	Макс. Енергетика$J/kg$
Стародавнє залізо	0,03	70	0,01	7 800	1.3
Сучасна пружинна сталь	0.3	700	1.0	7 800	130
Тисова деревина	0.3	120	0.5	600	900
Сухожилля	8.0	70	2.8	1 100	2,500
Гума	300	7	10.0	1 200	8 000

Площа до межі текучості називається модулем пружності, а загальна площа до руйнування називається модулем в'язкості; вони показані на малюнку 13. Термін «модуль» використовується тому, що одиницями енергії деформації на одиницю об'єму є$N-m/m^3$ або$N/m^2$, які такі ж, як напруга або модуль пружності. Термін «стійкість» натякає на поняття, що до моменту врожайності матеріал не піддається впливу прикладеного напруги і при розвантаженні повернеться до початкової форми. Але коли деформація перевищує межу текучості, матеріал деформується необоротно, так що деяка залишкова деформація збережеться навіть після розвантаження. Модуль стійкості - це кількість енергії, яку матеріал може поглинути, не зазнаючи шкоди. Аналогічно, модуль в'язкості - це енергія, необхідна для повного руйнування матеріалу. Матеріали, що демонструють хорошу ударостійкість, як правило, мають високі модулі в'язкості.

Малюнок 13: Модулі стійкості та в'язкості.

У таблиці 1 (J.E. Gordon, Структури, або Чому речі не падають, Plenum Press, Нью-Йорк, 1978) перераховуються значення поглинання енергії для ряду поширених матеріалів. Відзначимо, що натуральні і полімерні матеріали можуть забезпечити надзвичайно високе поглинання енергії на одиницю ваги.

Під час навантаження площа під кривою напруження-деформація - це енергія деформації на одиницю об'єму, поглинену матеріалом. І навпаки, площа під кривою розвантаження - це енергія, що виділяється матеріалом. У пружному діапазоні ці області рівні і ніяка чиста енергія не поглинається. Але якщо матеріал завантажується в пластиковий діапазон, як показано на малюнку 14, енергія, що поглинається, перевищує енергію, що виділяється, і різниця розсіюється у вигляді тепла.

Малюнок 14: Втрати енергії = площа під напружено-деформованим контуром.

Стиснення

Вищезазначене обговорення стосується насамперед простого натягу, тобто одновісного навантаження, що збільшує міжатомну відстань. Однак до тих пір, поки навантаження досить малі (напруги менше пропорційної межі), у багатьох матеріалах описані вище співвідношення застосовуються однаково добре, якщо навантаження розміщуються так, щоб поставити зразок на стиск, а не розтяг. Вираз для деформації та заданого навантаження$\delta = PL/AE$ застосовується так само, як і при розтягуванні, з негативними значеннями для$\delta$ та$P$ вказівкою на стиснення. Далі модуль$E$ однаковий за напругою і стисненням до хорошого наближення, а крива напруження-деформація просто тягнеться прямою лінією в третій квадрант, як показано на малюнку 15.

Малюнок 15: Крива напруження-деформація при розтягуванні і стисненні.

Існують деякі практичні труднощі при виконанні напружено-деформованих випробувань при стисненні. Якщо при випробуванні на розтяг помилково застосовані надмірно великі навантаження, можливо, неправильними налаштуваннями на випробувальній машині, зразок просто ламається, і випробування потрібно повторити з новим зразком. Але при стисненні помилка може легко пошкодити тензодатчик або інші чутливі компоненти, оскільки навіть після відмови зразка навантаження не обов'язково знімаються.

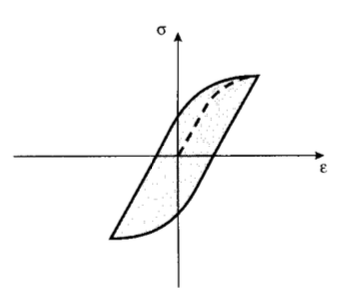
Зразки, завантажені циклічно так, щоб чергувати розтяг і стиснення, можуть проявляти петлі гістерезису, якщо навантаження досить високі, щоб викликати пластичний потік (напруги вище межі текучості). Закрита область в петлі, показана на малюнку 16, - це енергія деформації на одиницю об'єму, що виділяється у вигляді тепла в кожному циклі навантаження. Це добре відома тенденція дроту, який згинається вперед і назад, щоб стати досить гарячим в області пластичного вигину. Температура зразка підвищиться відповідно до величини цього внутрішнього теплоутворення та швидкості, з якою тепло може бути видалено провідністю всередині матеріалу та конвекцією з поверхні зразка.

Малюнок 16: Петля гістерезису.

Відмова зразків шляхом розтріскування гальмується при стисненні, оскільки тріщини будуть закриті, а не відкриваються напруженим станом. Ряд важливих матеріалів набагато сильніше в стисненні, ніж при розтягуванні з цієї причини. Бетон, наприклад, має хорошу міцність на стиск і тому знаходить широке застосування в будівництві, в якому домінуючими напруженнями є стискання. Але вона по суті не має міцності на розтяг, як свідчать тріщини в тротуарах і фундаментах будівель: розтягуючі напруги з'являються в міру осідання цих конструкцій, а тріщини починаються при дуже низькому розтягуванні в неармованому бетоні.

Посилання

1. Боєр, H.F., Атлас кривих напруження-деформації, ASM International, Metals Park, Огайо, 1987.

2. Кортні, Т.Х., Механічна поведінка матеріалів, Макгроу-Хілл, Нью-Йорк, 1990.

3. Hayden, HW, WG Moffatt and J Wulff, Структура та властивості матеріалів: Vol. III Механічна поведінка, Вілі, Нью-Йорк, 1965.

Вправа$\PageIndex{1}$

На малюнку нижче показана інженерна крива напруження-деформації для чистого полікристалічного alu- minum; числові дані для цього малюнка знаходяться у файлі aluminum.txt, який можна імпортувати в електронну таблицю або інше програмне забезпечення для аналізу. Для цього матеріалу визначте (а) модуль Юнга, (б) межа текучості зсуву 0,2%, (c) граничну міцність на розрив (UTS), (d) модуль пружності та (e) модуль в'язкості.

Вправа$\PageIndex{2}$

Розвиваємо відносини, наведені в рівнянні 1.4.6:

$$\sigma_t = \sigma_e (1 + \epsilon_e) =\sigma_e \lambda, \epsilon_t = \ln (1 + \epsilon_e) = \ln \lambda \nonumber$$

Вправа$\PageIndex{3}$

Використовуючи співвідношення рівняння 1.4.6, побудуйте істинну криву напруження-деформації алюмінію (за даними вправи$\PageIndex{1}$) аж до деформації формування шиї.

Вправа$\PageIndex{4}$

Перерахуйте результати попередньої задачі за допомогою осей журналів, як на малюнку 9 для визначення параметрів$A$ та$n$ в Рівнянні 1.4.8 для алюмінію.

Вправа$\PageIndex{5}$

Використовуючи рівняння 1.4.8 з параметрами$A$ = 800 МПа$n = 0.2$, побудуйте інженерну криву напруження-деформації до деформації$\epsilon_e = 0.4$. Чи є матеріал горловини? Поясніть, чому крива є або не дійсна при деформаціях поза шиєю.

Вправа$\PageIndex{6}$

Використовуючи параметри попередньої задачі, використовуйте умову$(d\sigma_e/d\epsilon_e)_{\text{neck}} = 0 to show that the engineering strain at necking is \(\epsilon_{e, neck} = 0.221$.

Вправа$\PageIndex{7}$

Скористайтеся конструкцією Considere (ділянка$\sigma_t$ проти$\lambda$, як на рис. 10), щоб перевірити результат попередньої задачі.

Вправа$\PageIndex{8}$

Еластомери (гума) мають напружено-деформовані відносини виду

$$\sigma_e = \dfrac{E}{3} \left (\lambda - \dfrac{1}{\lambda^2} \right ),\nonumber$$

де$E$ - початковий модуль. Скористайтеся конструкцією Consid`ere, щоб показати, чи буде цей матеріал шию, або малювати.

Вправа$\PageIndex{9}$

Показати, що матеріал закону влади (той, що підпорядковується рівнянню 1.4.8) шийки, коли справжня деформація$\epsilon_t$ стає рівною показнику деформаційного зміцнення$n$.

Вправа$\PageIndex{10}$

Показати, що UTS (інженерне напруження при початковій шийці) для матеріалу закону влади (рівняння 1.4.8)

$$\sigma_f = \dfrac{An^n}{e^n}\nonumber$$

Вправа$\PageIndex{11}$

Показати, що енергію деформації$U = \int \sigma \ d \epsilon$ можна обчислити за допомогою інженерних або істинних значень напружень і деформацій, з однаковим результатом.

Вправа$\PageIndex{12}$

Показати, що енергія деформації, необхідна для шийки матеріалу закону влади (Рівняння 1.4.8)

$$U = \dfrac{An^{n + 1}}{n + 1}\nonumber$$