9.4: Динамічна оснащення
- Page ID
- 32891
Конспекти лекцій обмежені статичними та квазістатичними задачами. Однак характер задачі оснащення вимагає розгляду повного динамічного аналізу. Припустимо, що навантаження двухбарной системи контролюється навантаженням. На ділянці АВ є стійкий шлях рівноваги. При\(\bar{P}_{\text{max}} = \frac{2}{3 \sqrt{3}}\bar{\delta}^3\) досягненні система миттєво перескакує до наступної точки рівноваги F в статичному розчині. Величина сили однакова, але відповідне зміщення визначається з рішення кубічного рівняння
\[\frac{2}{3\sqrt{3}}\bar{\delta}^3 = \delta \bar{\delta}^2 − \delta^3 \]
Це рівняння має три реальних кореня
\[\delta_1 = \frac{\bar{\delta}}{\sqrt{3}}, \delta_2 = \delta_3 = − \frac{2 \bar{\delta}}{\sqrt{3}} \]
Додаючи сили інерції в рівняння рівноваги, процес оснащення відбувається в часі. Барна система спочатку прискорюється на частині BCD спадної сили, а потім сповільнюється на зростаючій частині DEF.
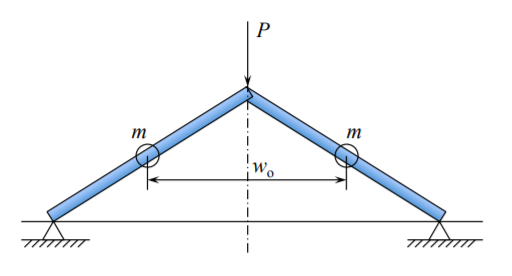
Динамічне рішення прямо вперед, якщо розподілена маса стрижня згорнута в дві дискретні точкові маси\(m = lA\rho\), як показано на малюнку (\(\PageIndex{1}\)).
Додаючи сили інерції д'Аламбера в статичну рівновагу, рівняння (9.3.5), отримують
\[−P − 2m \frac{\ddot{w}_o}{2} = 2N \frac{w_o}{l} \label{10.52}\]
де зараз\(P\) позитивно в напрузі.
Усунувши осьову силу\(N\) в прутках між рівняннями (9.3.4) та\ ref {10.52}, отримують наступне диференціальне рівняння
\[−\bar{P} − \frac{l^2 \rho}{E} \ddot{\delta} = \delta [ \delta^2 − \bar{\delta}^2 ] \label{10.53}\]
де точка позначає диференціацію по відношенню до часу. Зручно вводити безрозмірний час\(\bar{t} = \frac{t}{t_1}\), де\(t_1 = \frac{l}{c}\) -\(c^2 = \frac{E}{\rho}\) еталонний час, і швидкість поздовжньої хвилі напруги в барі. У системі, керованій силою, збудливий термін постійний\(\bar{P} = \frac{2}{3 \sqrt{3}}\bar{\delta}^3\). У новій безрозмірній координаті Equation\ ref {10.53} набуває вигляду
\[−\bar{P} − \ddot{\delta} = \delta^3 − \bar{\delta}^2 \delta \label{10.54}\]
де точка позначає диференціацію щодо безрозмірного часу\(\bar{t}\). Використовуючи ланцюгове правило диференціації,
\[\ddot{\delta} = \frac{d \dot{\delta}}{d\bar{t}} = \frac{d \dot{\delta}}{d\delta} \frac{d \delta}{d\bar{t}} = \frac{d \dot{\delta}}{d\delta} \dot{\delta} \label{10.55}\]
можна отримати рішення на фазовій площині\((\delta, \dot{\delta}\)) швидше засмаги в часовій області. Підставляючи рівняння\ ref {10.55} на рівняння\ ref {10.54}, отримано наступне рівняння
\[−\bar{P} d\delta − \dot{\delta}d \dot{\delta} = (\delta^3 − \bar{\delta}^2 \delta ) d\delta \]
які можуть бути легко інтегровані, щоб дати
\[−\bar{P} \delta − \frac{1}{2} \dot{\delta}^2 = \frac{\delta^4}{4} − \frac{\bar{\delta^2}\delta^2}{2} + C \label{10.57}\]
Константа інтеграції\(C\) визначається з початкової умови, що швидкість\(\dot{\delta}\) дорівнює нулю при досягненні прогину\(\delta = \frac{1}{\sqrt{3}}\) (точка В). Рішенням для швидкості\(\dot{\delta}\) є
\[\dot{\delta} = 2\bar{\delta}^2 \sqrt{−P \left(\frac{\delta}{\bar{\delta}}\right) + \frac{1}{2}\left(\frac{\delta}{\bar{\delta}}\right)^2 − \frac{1}{4} \left(\frac{\delta}{\bar{\delta}}\right)^4 + \frac{1}{12}} \label{10.58}\]
З точки зору нормованої швидкості\(\frac{\dot{\delta}}{2 \bar{\delta}^2} = \bar{v}\) та нормованого відхилення\(\eta = \frac{\delta}{\bar{\delta}}\) рівняння\ ref {10.58} читає
\[\bar{v} = \sqrt{−\frac{2}{3 \sqrt{3}}\eta + \frac{1}{2}\eta^2 − \frac{1}{4}\eta^4 + \frac{1}{12}} \label{10.59}\]
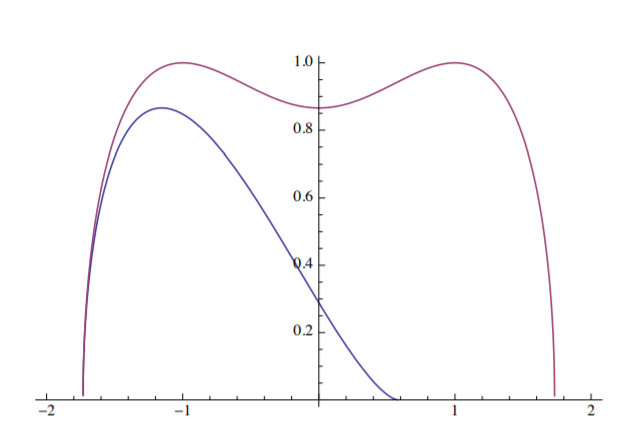
Сюжет\(\bar{v}\) versus\(\eta\) показаний на малюнку (\(\PageIndex{2}\)).
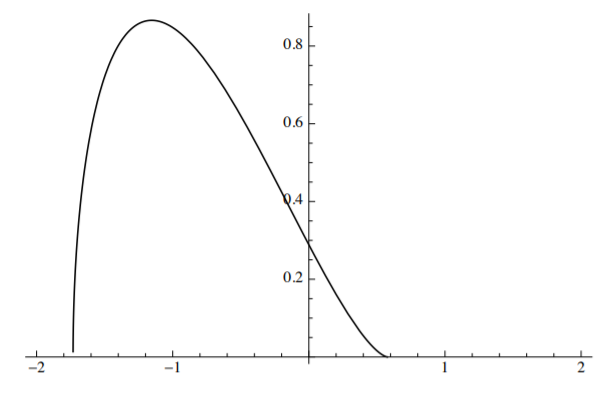
Многочлен\(\eta\) під квадратним коренем у Equation\ ref {10.59} має два дійсних кореня, at\(\eta = \frac{1}{\sqrt{3}}\) і\(\eta = − \sqrt{3}\). Динамічний рух починається з B, збільшується повільно, досягає максимуму в F і швидко падає до нуля в точці G з координатою\(\eta_f = \sqrt{3}\). Зверніть увагу, що динамічний прогин значно перевершує прогин, досягнутий у статичній задачі\(\eta_{\text{stat}} = \frac{2}{\sqrt{3}} = 1.15\).
На завершальному етапі, коли рух системи припиняється, в штанзі зберігається достатня енергія розтягування для початкової вільної вібрації зі\(\bar{P}\) знятим терміном форсування. Розв'язок цієї фази задається рівнянням\ ref {10.57} with\(\bar{P} = 0\), і новою константою інтеграції\(C_1 = \frac{3}{4}\) таким чином, що досягається неперервність швидкості. Сюжет вільної вібрації системи, що регулюється
\[\bar{v} = \sqrt{\frac{1}{2}\eta^2 − \frac{1}{4}\eta^4 + \frac{3}{4}} \]
показано на малюнку (\(\PageIndex{3}\)), у порівнянні з динамічним скрізним графіком.