9.1: Найвища колона

У 1757 році швейцарський математик Леонард Ейлер представив відоме рішення для вигину штифтової колони при стискаючому навантаженні на її кінці. Також він сформулював і вирішив набагато складнішу проблему затиснутої колони, завантаженої власною вагою. Практичне питання полягало в тому, якою висотою може бути призматична колона, перш ніж вона застебнеться під власною вагою. Для того щоб сформулювати цю задачу, рівняння рівноваги балки/колони в осьовому напрямку необхідно переглянути повторно. Замість рівняння$N^{\prime} = 0$ або$N =$ конст, ми повинні припустити, що$q$ на одиницю довжини є сила тіла$q = A\rho$, де$A$ - площа поперечного перерізу колони і$\rho$ її масова щільність. Тоді рівновага в осьовому напрямку вимагає, щоб

$$N^{\prime} = q \quad \text{ or } \quad N = qx + C$$

У системі координат, зображеній на малюнку ($\PageIndex{1}$), осьова сила повинна дорівнювати нулю при$x = l$.

Малюнок$\PageIndex{1}$: Колонка завантажена на її кінчику (зліва) і завантажена власною вагою (праворуч).

Розподіл осьової сили по довжині колони становить

$$N(x) = −q(l − x)$$

де знак мінус вказує на те, що$N$ є стискаючою силою. Як і раніше, вхідні параметри задачі є$E$,$I$$q$ а невідомою є критична довжина$l_c$.

Виведення задачі вигину для класичної колони, представленої в розділі 8, все ще є дійсним, але осьова сила в Рівнянні (8.3.11) більше не є постійною і, отже, повинна зберігатися всередині інтеграла.

Для цієї проблеми першою варіацією загальної потенційної енергії є

$$\delta \prod = − \int_{0}^{l} M \delta w^{\prime\prime} dx + \int_{0}^{l} q(l − x)w^{\prime} \delta w^{\prime} dx \label{10.3}$$

Інтегруючи праву частину Equation\ ref {10.3} по частині, отримуємо

$$\int_{0}^{l} M^{\prime\prime} + q(l − x)w^{\prime} \delta w dx + \text{ Boundary terms } = 0$$

де

$$\text{ Boundary terms } = −\left. M \delta w^{\prime} \right|^{l}_{0} + \left. M^{\prime} \delta w \right|^{l}_{0} + q(l − x) w^{\prime} \delta w$$

в$x = 0$,$\delta w = \delta w^{\prime} = 0$; і в$x = l$,$M = 0$,$V = M^{\prime} = 0$ і$l − x = 0$. Тому граничні терміни зникають (див. Посвячення в розділі 2.5). Використовуючи закон пружності$M = −EIw^{\prime\prime}$, локальне рівняння рівняння рівноваги для колони самостійного вигину стає

$$EI \frac{d^4w}{dx^4} + \frac{d}{dx} \left[ q(l − x) \frac{dw}{dx} \right] = 0$$

Інтегруючи один раз, ми отримуємо

$$EI \frac{d^3w}{dx^3} + q(l − x)dw = 0 \label{10.7}$$

Константа інтеграції дорівнює нулю, оскільки сила зсуву зникає на вільному кінці$x = l$. Керуючим рівнянням є лінійне диференціальне рівняння третього порядку зі змінним коефіцієнтом. Рішення більше не представлено гармонійною функцією. Спосіб вирішення проблеми полягає у введенні двох нових змінних.

$$\xi = \frac{2}{3} \sqrt{ \frac{q(l − x)^3}{EI}}, \quad u = \frac{dw}{d\xi}$$

Потім рівняння\ ref {10.7} перетворюється на рівняння Бесселя

$$\frac{d^2 u}{d\xi^2} + \frac{1}{\xi} \frac{du}{d\xi} + (1 − \frac{1}{9\xi^2} )u = 0$$

Опускаючи деталі розрахунку, критична довжина колони виявляється

$$l^3_c = \frac{9EI}{4q} j^2_{\frac{1}{3}}$$

де$j_{\frac{1}{3}} = 1.866$ - корінь функції Бесселя третього роду. Нарешті

$$l^3_c = 7.837 \frac{EI}{q}$$

Загальна вага матеріалу колони становить$N_c = l_cq$. У перерахунку на загальну вагу критична довжина дорівнює

$$l^2_c = 7.84 \frac{EI}{N_c} \label{10.12}$$

Для порівняння довжина вільно затиснутої колони при вигині, навантаженої однаковою вагою, дорівнює

$$l^2_c = \frac{\pi^2}{4} \frac{EI}{N_c} = 2.47 \frac{EI}{N_c}$$

Дно обох колон бачить однакову вагу, але критична довжина колони, що зазнає самовигинається, в$\sqrt{\frac{7.84}{2.47}} = 1.78$ рази вище аналогічного перерізу колони, завантаженої на її кінчику.

Приклад$\PageIndex{1}$

Сталева трубчаста щогла міцно вбудована в фундамент і вільна на його вершині. Циліндр товщиною$t = 3$ мм і має радіус$R = 50$ мм. Яка критична довжина щогли, щоб застібатися під власною вагою?

Загальна вага щогли дорівнює

$$N_c = Al \rho$$

де$A$ - площа поперечного перерізу,$A = 2\pi Rt$. Другим моментом інерції тонкостінної труби є$I = \pi R^3 t$. З рівняння\ ref {10.12}

$$l^2_c = 7.84 \frac{E \pi R^3 t}{2 \pi Rtl_c \rho}$$

з якого виходить

$$l_c = \sqrt[3]{\frac{3.92ER^2}{\rho}} = 65 m$$

Вищевказане рішення стосується призматичної колони постійного перерізу.

Приблизний розчин може бути отриманий з умови Треффца$\delta^2 \prod = 0$. Починаючи з Equation\ ref {10.3} і виконуючи другу варіацію, отримуємо

$$EI \int_{0}^{l} \delta w^{\prime\prime} \delta w^{\prime} dx + \int_{0}^{l} q(l − x)\delta w^{\prime} \delta w dx$$

Тоді критична сила стискаючого тіла

$$q = EI \frac{\int_{0}^{l} \phi^{\prime\prime} \phi^{\prime\prime} dx}{\int_{0}^{l} (l − x)\phi^{\prime}\phi^{\prime} dx} \label{10.18}$$

У порівнянні зі стандартною формулою Trefftz для стовпчика, завантаженого наконечником,$(l − x)$ в знаменнику є термін. Як приклад розглянемо найпростішу параболічну форму прогину.

$$\phi = x^2$$

$$\phi^{\prime} = 2x$$

$$\phi^{\prime\prime} = 2$$

Вводячи вищевказаний вираз в Equation\ ref {10.18}, критична вага вигину на одиницю довжини дорівнює

$$q = \frac{12EI}{l^3}$$

Помилка в цьому наближенні -$\frac{12 − 7.837}{7.837} = 53\%$ це не добре. В якості другого випробування розглянемо функцію степеневої форми з дробовим показником.$\alpha$

$$\phi = x^{\alpha}$$

$$\phi^{\prime} = \alpha x^{\alpha−1}$$

$$\phi^{\prime\prime} = \alpha(\alpha − 1)x^{\alpha−2}$$

Отриманий розчин

$$q = \frac{2EI}{l^3} \frac{\alpha(\alpha − 1)(2\alpha − 1)}{2\alpha − 3}$$

Критичний параметр вигину досягає мінімумів при$\alpha = 1.75$. Мінімальне навантаження на вигин

$$q_{\text{min}} = 9.8 \frac{EI}{l^3}$$

Похибка зменшена вдвічі, але вона все ще велика на 25%. У третій спробі розглянемо тригонометричну функцію

$$\phi = 1 − \cos \frac{\pi x}{2l} \label{10.24a}$$

$$\phi^{\prime} = \left(\frac{\pi}{2l}\right) \sin \frac{\pi x}{2l}$$

$$\phi^{\prime\prime} = \left( \frac{\pi}{2l} \right)^2 \cos \frac{\pi x}{2l} \label{10.24c}$$

Крім задоволення затиснутого кінематичного стану при$x = 0$, форма косинуса дає нульовий згинальний момент вгорі. Підставляючи рівняння\ ref {10.24a} -\ ref {10.24c} в умову Треффца, Рівняння (10.18), отримано наступний розв'язок закритої форми

$$q = \frac{EI}{l^3} \frac{\pi^4}{2(\pi^2 − 4)} = 8.29 \frac{EI}{l^3}$$

який відрізняється лише на 6% від точного розчину. Справжня форма колони, яка пряжиться власною вагою, - це функція Бесселя, але тригонометрична функція забезпечує дуже хороше наближення.

Вже понад 200 років рішення Ейлера викривлення колони під власною вагою залишається безпроблемним. У 1960 році Келлер і Ніордсон задалися питанням, на скільки можна збільшити висоту колони. Якщо ж обсяг матеріалу розподіляється як постійний перетин призматичної конструкції радіусом$r = 0.1$ м, то довжина колони буде

$$l = \frac{V}{\pi r^2} = \frac{1}{\pi 0.1^2} = 32 m \nonumber$$

і вага на одиницю довжини нерухомого стовпця буде

$$q = \frac{V}{l} = \frac{7.8 \times 10^4}{32} = 24 N/m \nonumber$$

За допомогою Equation\ ref {10.12} ми можемо перевірити, чи залишиться така колонка або застібатися під власною вагою

$$l^2_c = 7.84 \frac{EI}{N} \nonumber$$

де$I = \frac{\pi r^4}{4}$,$N = V \rho$ і$E = 2.1 \times 10^{11} N/m^2$. Підставляючи вищевказані значення, критична довжина стає$l_c = 26$ м, а це означає, що призматична колона об'ємом 32 м буде загнута і не може бути зведена. При формуванні колони по малюнку ($\PageIndex{2}$) її довжина може бути збільшена в рази$86/26 = 3.3$.

Якщо перетин змінний, це питання призвело до дуже складної математичної задачі. Деякі аспекти цього рішення вивчаються досі. Проблема добре поставлена, якщо оптимальне рішення шукає при постійному, заданому обсязі матеріалу. Простого закритого розв'язку задачі не існує, тому відповідь отримується шляхом числової оптимізації, див. Рисунок ($\PageIndex{2}$).

Малюнок$\PageIndex{2}$: Форма найвищої колони.

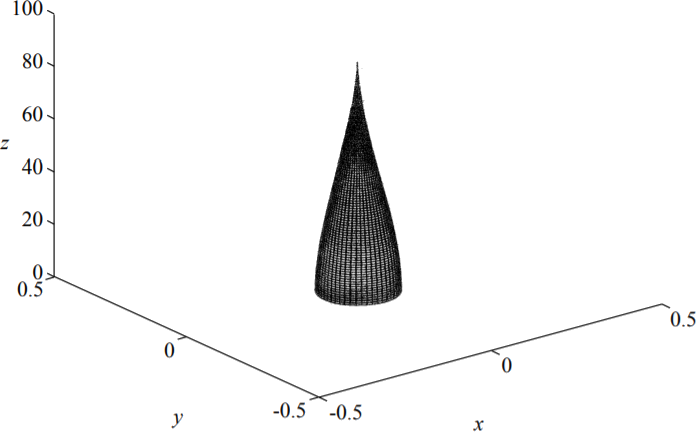
Зверніть увагу, що висота стовпця була зменшена відповідно до розміру сторінки. Щоб дати вам уявлення, сталева колона загальним об'ємом 1,0 м$^3$ і оголеним радіусом 10 см могла бути висотою$l = 86$ до м.