8.7: Перехід режиму (розширений)
- Page ID
- 32969
Рівняння рівноваги моменту
Для штифтової опорної колони форма недосконалості\(\bar{w}(x)\) та деформація\(w(x)\) задовольняють рівнянню рівняння рівноваги моменту
\[EIw^{\prime \prime} + P w = EI\bar{w}^{\prime \prime} \label{9.77}\]
Розв'язки повинні задовольняти граничним умовам
\[\begin{align*} w(0) &= 0 \\[4pt] w^{\prime \prime}(0) &= 0 \\[4pt] w(l) &= 0 \\[4pt] w^{\prime \prime}(l) &= 0 \end{align*}\]
Звичайно, розчини також повинні задовольняти безперервним умовам:\(w(x)\) і бути\(w^{\prime}(x)\) безперервними по всій довжині колони, а саме в розчині не відбувається жодного кроку або зламу.
Ми можемо розширити недосконалість\(\bar{w}(x)\) у рядах Фур'є як
\[\bar{w}(x) = \sum^{\infty}_{n=1} A_n \sin \frac{n \pi x}{l} \label{9.79}\]
Коефіцієнти\(A_n\) можуть бути визначені шляхом перетворення Фур'є\(\bar{w}\):
\[A_n = \frac{2}{l} \int_{0}^{l} \bar{w}(x) \sin \frac{n \pi x}{l} dx \]
Деформацію\(w(x)\) під навантаженням\(P\) можна записати як підсумовування повної множини рядів Фур'є.
\[w(x) = \sum^{\infty}_{n=1} B_n \sin \frac{n \pi x}{l} \label{9.81}\]
де\(B_n\) можна визначити за рівнянням\ ref {9.77}.
Рівняння\ ref {9.77} тепер стає
\[ -\sum^{\infty}_{n=1} B_n \left(\frac{n \pi} {l} \right)^2 \sin \frac{n \pi x}{l} + \frac{P}{EI} \sum^{\infty}_{n=1} B_n \sin \frac{n \pi x}{l} = - \sum^{\infty}_{n=1} A_n \left(\frac{n \pi} {l} \right)^2 \sin \frac{n \pi x}{l}\]
Щоб рівняння трималося, коефіцієнти повинні задовольняти
\[−B_n \frac{n^2 \pi^2} {l^2} + \frac{P}{EI} B_n = −A_n \frac{n^2 \pi^2} {l^2} \]
Вирішуємо за\(B_n\), отримуємо
\[B_n = A_n \frac{1}{1 − \bar{P}/n^2} \]
тут, ми визначили\(\bar{P} = P/P_c\) і\(P_c = \frac{\pi^2 EI}{l^2}\). Отже, деформація\(w(x)\) є
\[w(x) = \sum^{\infty}_{n=1} A_n \frac{1}{1 − \bar{P}/n^2} \sin \frac{n \pi x}{l} \]
Рішення говорить нам, що таке форма деформації, але це не говорить нам нічого про стабільність рівноважної форми. Якщо ми хочемо вивчити стабільність, ми повинні використовувати метод потенційної енергії.
Метод потенційної енергії
Під\(P\) навантаженням загальна потенційна енергія системи колон дорівнює (завдяки рівнянню (9.2.1) в главі 9):
\[\prod = \frac{EI}{2} \int_{0}^{l} (w^{\prime \prime} − \bar{w}^{\prime \prime})^2 dx − \frac{P}{2} \int_{0}^{l} (w^{\prime 2} − \bar{w}^{\prime 2}) dx \]
Підставляємо рівняння\ ref {9.79} і\ ref {9.81} в нього, ми маємо
\[\begin{align*} \prod &= \frac{EI}{2} \int_{0}^{l} (w^{\prime \prime} − \bar{w}^{\prime \prime})^2 dx − \frac{P}{2} \int_{0}^{l} (w^{\prime 2} − \bar{w}^{\prime 2}) dx \\[4pt] &= \frac{EI}{2} \int_{0}^{l} \left[ -\sum^{\infty}_{n=1} B_n \left(\frac{n \pi} {l} \right)^2 \sin \frac{n \pi x}{l} + \sum^{\infty}_{n=1} A_n \left(\frac{n \pi} {l} \right)^2 \sin \frac{n \pi x}{l} \right]^2 dx - \frac{P}{2} \int_{0}^{l} \left\{ \left[ \sum^{\infty}_{n=1} B_n \left(\frac{n \pi} {l} \right) \cos \frac{n \pi x}{l} \right]^2 - \left[ \sum^{\infty}_{n=1} A_n \left(\frac{n \pi} {l} \right) \cos \frac{n \pi x}{l} \right]^2 \right\} dx \\[4pt] &= \frac{\pi^4 EI}{4l^3} \sum^{\infty}_{n=1} (B_n - A_n)^2 n^4 - \frac{\pi^2 P}{4l} \sum^{\infty}_{n=1} B_n^2 n^2 + \frac{\pi^2 P}{4l} \sum^{\infty}_{n=1} A_n^2 n^2 \\[4pt] &= \frac{\pi^2 P_c}{4l} \left\{ \sum^{\infty}_{n=1} [(B_n - A_n)^2 n^4 - \bar{P} (b_n^2 - a_n^2) n^2] \right\} \end{align*}\]
Для спрощення інтеграції використовується ортогональність рядів Фур'є.
Для того щоб отримати рівноважний розчин, потрібна перша похідна потенційної енергії
\[\frac{\partial \prod}{\partial B_n} = 0 \quad \rightarrow \quad B_n = A_n \frac{1}{1 − \bar{P}/n^2} \label{9.88}\]
який точно такий же, як і рішення, дане рішенням рівняння рівняння рівноваги.
Щоб побачити стабільність розчину, нам потрібна друга похідна потенційної енергії
\[\frac{\partial^ \prod}{\partial B_n^2} > 0 \quad \rightarrow \quad \bar{P} < n^2 \label{9.89}\]
Ми можемо побачити наступні моменти безпосередньо з Рівняння\ ref {9.88} і\ ref {9.89}:
- Критичне навантаження на вигин для\(n^{th}\) режиму є\(P_c = \frac{n^2\pi^2 EI}{l^2}\).
- Режими, які\(n^2 > \bar{P}\) задовольняють, знаходяться в стабільній рівновазі.
- Для режимів, які задовольняють\(n^2 < \bar{P}\), ми все ще можемо вирішити для значення\(B_n\), але ці режими нестабільні і будуть вписатися в плюс або мінус нескінченність.
Приклад\(\PageIndex{1}\)
Недосконалість\(\bar{w}(x)\) складається тільки з перших двох режимів, а саме
\[\bar{w}(x) = A_1 \sin \frac{\pi x}{l} + \sin \frac{2 \pi x}{l} \]
Якщо\(A_1 = 0\), нульова точка знаходиться в центрі стовпчика. Якщо\(A_1 \neq 0\), нульова точка зміщується на відстань\(u\). \(u\)дається
\[u = \frac{\sin^{−1} \frac{A_1}{2}}{\pi} l , \quad 0 \leq A_1 \leq 2 \]
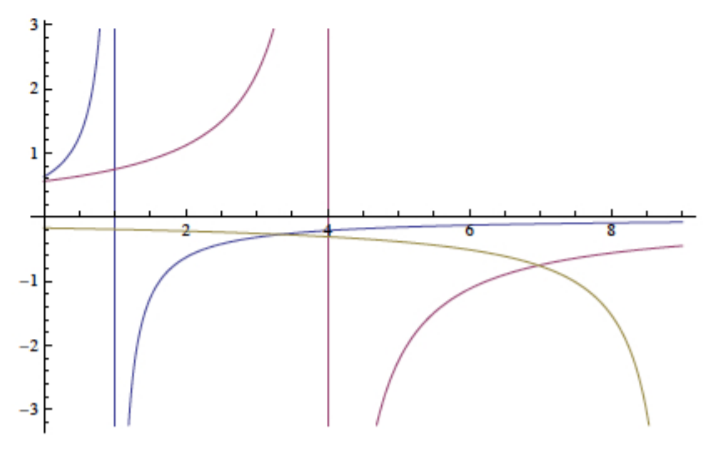
Амплітуди деформації проти кривих навантаження побудовані на рисунку (\(\PageIndex{1}\)) для випадку\(A_1 = 0.5\), Рисунок (\(\PageIndex{2}\)) для\(A_1 = 1\) та Рисунок (\(\PageIndex{3}\)) для\(A_1 = 1.5\).
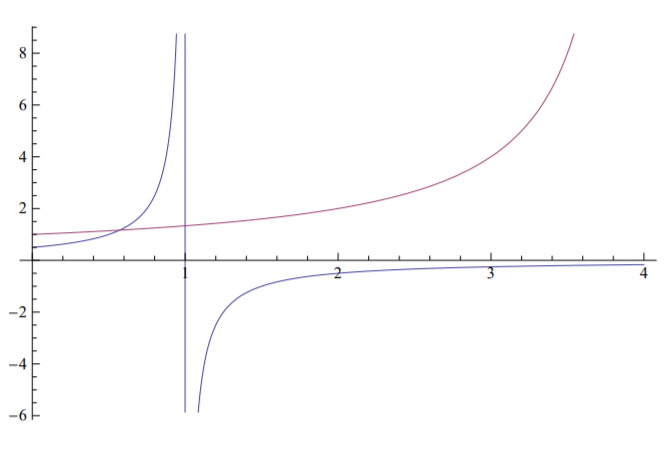
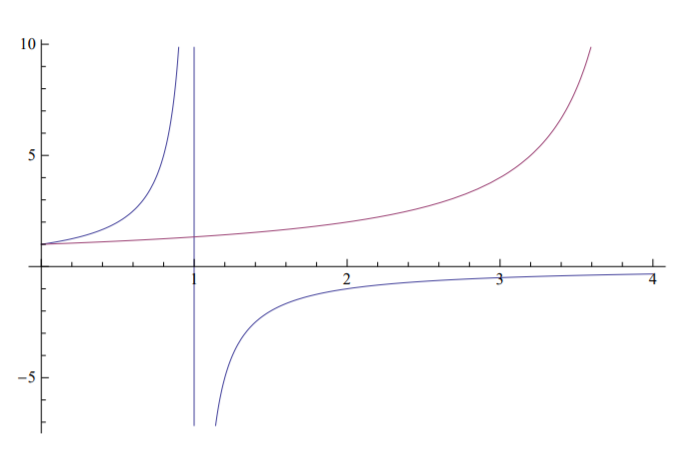
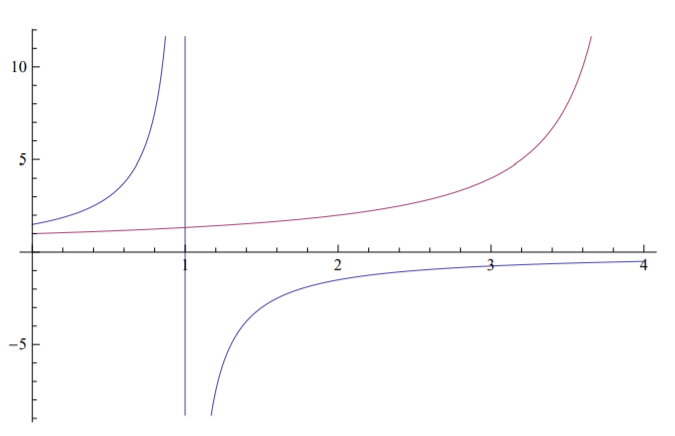
Приклад\(\PageIndex{2}\)
Недосконалість полягає в такій формі, що нульова точка зміщується, тоді як обидва перерізи самосиметричні. Таку форму можна охарактеризувати як
\[\bar{w}(x) = \begin{cases} \sin \frac{\pi x}{\eta l} & 0 < x < \eta l \\ − \frac{1 − \eta}{\eta} \sin \frac{\pi(x − \eta l)}{(1 − \eta)l} & \eta l < x < l \end{cases} \label{9.92}\]
де\(0.5 \leq \eta \leq 1\). Коли\(\eta = 0.7\),\(\bar{w}(x)\) можна розширити в рядах Фур'є як:
\[\bar{w}(x) = 0.634 \sin \frac{\pi x}{l} + 0.563 \sin \frac{2 \pi x}{l} − 0.174 \sin \frac{3 \pi x}{l} + 0.071 \sin \frac{4 \pi x}{l} + \dots \]
Як і очікувалося, в цьому випадку домінують перші два режими, але в розширенні все ще є більш високі режими.
Ми будуємо амплітуди режиму проти навантаження на рисунку (\(\PageIndex{4}\)). Якщо навантаження\(\bar{P} > 4\), наприклад\(\bar{P} = 7.5\), амплітуда III режиму стає найбільшою. Отже, вирішена форма деформації більше схожа на режим III, хоча початкова недосконалість, здається, не має нічого спільного з режимом III. Проте ця форма дуже нестійка; так як і режим I\(\bar{P} > 2^2\), і режим II знаходяться в нестійкому рівновазі. При такому навантаженні режим I і режим II будуть посилюватися в геометричній прогресії.