8.6: Пластикові вигину колон

Last updated
Save as PDF

Page ID: 32937

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Розглянемо штифт-колону, для якої критична навантаження на вигин

\[P_c = \frac{\pi^2 EI}{l^2}\]

Відповідне критичне напруження\(\sigma_c\) вигину

\[\sigma_c = \frac{P_c}{A} = \frac{\pi^2 E}{l^2} \frac{I}{A} \label{9.69}\]

де\(A\) - площа поперечного перерізу. Зверніть увагу, що напруга розраховується по попередньо вигинає, первинному шляху рівноваги, для якого немає вигину. Позначивши\(\rho\) радіусом обертання\(A \rho^2 \equiv I\), рівняння\ ref {9.69} можна переписати через коефіцієнт стрункості\(\beta = l/\rho\)

\[\sigma_c = \pi^2 E \frac{1}{\beta^2} \label{9.70}\]

Напруга вигину невелика для довгої, стрункої колони і швидко зростає для коротких колон. При деякій критичній довжині стовпця межа текучості матеріалу\(\sigma_y\) буде досягнута, Рисунок (\(\PageIndex{1}\)).

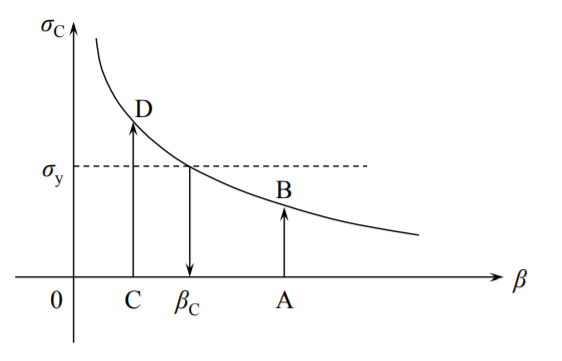
8.6.1.png — Малюнок\(\PageIndex{1}\): Гіперболічна залежність напруги вигин від коефіцієнта стрункості.

Критичний коефіцієнт стрункості, при якому напруга вигину досягає межі текучості матеріалу, отримано з Equation\ ref {9.70} шляхом встановлення\(\sigma_c = \sigma_y\)

\[\beta_c = \frac{l_c}{\rho} = \pi \sqrt{\frac{E}{\sigma_y}} \]

Щоб дати вам відчуття критичної стрункості, розглянемо стовп з м'якої сталі з\(E = 210\)\(\sigma_y = 250\) ГПа, МПа і квадратним перетином\(A = h^2\), для якого радіус обертання дорівнює\(\rho^2 = h^2/12\)

\[\left( \frac{l}{h} \right)_c = \pi \sqrt{\frac{E}{\sigma_y}} \cdot \frac{1}{2 \sqrt{3}} \approx 30 \]

Колони більш стрункі, ніж критичні, будуть пружно пряжатися перед тим, як поступитися (шлях AB). Коротша колона або кремезна колона дасть вигин перед вигином. Що буде з такими колонками? Вони будуть пластично деформуватися при осьовому стисненні і в кінцевому підсумку пряжкою в пластиковому діапазоні.

Джеррард (1948) розширив прогнозну здатність Equation\ ref {9.70} в пластичний діапазон шляхом заміни модуля пружності на дотичний модуль\(E_t = \frac{d\sigma}{d\epsilon}\)

\[(\sigma_c)_{\text{plastic}} = \pi^2 E_t \frac{1}{\beta^2}, \text{ for } \beta < \beta_c \label{9.73}\]

Наприклад, для пластичного матеріалу, який підкоряється правилу енергетичного зміцнення,

\[\sigma = B \cdot \epsilon^n \label{9.74a}\]

\[\frac{d\sigma}{d\epsilon} = nB\epsilon^{n−1} \label{9.74b}\]

Підставляючи рівняння\ ref {9.74a} -\ ref {9.74b} на рівняння\ ref {9.73}, критична деформація вигин\(\epsilon_c\) дорівнює

\[\epsilon_c = \frac{\pi^2 n}{\beta^2} \]

Використовуючи правило загартовування, напруга вигину становить

\[\sigma_c = B \left[ \frac{\pi^2 n}{\beta^2}\right]^n \]

У наведеному вище рівнянні\(B\) є амплітудою закону зміцнення і\(n\) є показником зміцнення. Для більшості конструкційних сталей\(n \approx 0.1-0.2\).

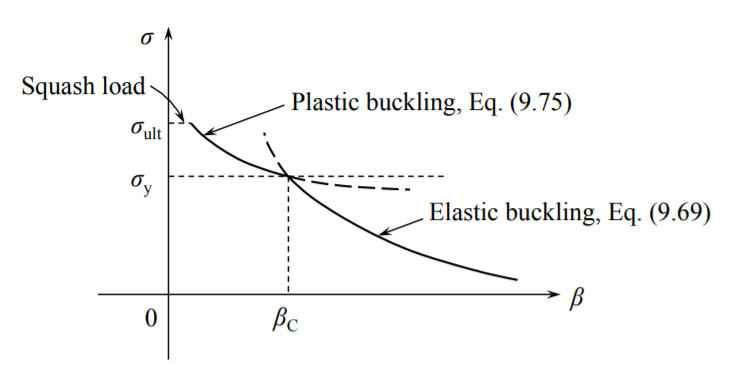
8.6.2.png — Малюнок\(\PageIndex{2}\): Діапазон еластичних і пластичних вигин.

Дуже короткі колони виходять за рамки елементарної теорії тонких і струнких балок. Вони ніколи не застібаються, а сплюснуть, як млинець.