8.4: Вплив структурних недосконалостей
- Page ID
- 32936
Розглянемо той же дискретний розпірка, що і в розділі 8.2. Цього разу жорсткий стрижень не прямий, а повертається на кут\(\theta_o\) до того, як буде застосовано вертикальне навантаження. При застосуванні навантаження колона піддається додатковому обертанню\(\theta\), виміряному від теоретичного вертикального напрямку, рис. (\(\PageIndex{1}\)).
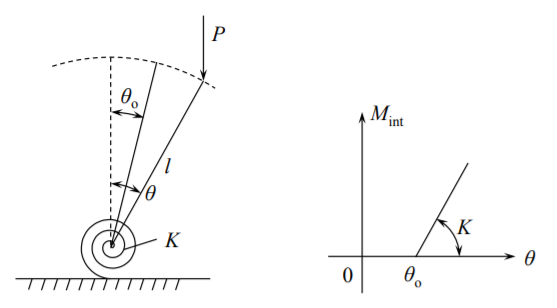
Проблема буде вирішуватися за допомогою локальної рівноваги. Зовнішній згинальний момент біля основи дорівнює
\[M_{\text{ext}} = Pl \sin \theta, \text{ for } \theta \geqslant \theta_o \]
де\(l \sin \theta\) знаходиться рука сили\(P\). У разі наближення малого кута\(M_{\text{ext}} = Pl \theta\). Внутрішній опір згинальний момент є
\[M_{\text{int}} = K(\theta − \theta_o) \]
Прирівнювання зовнішніх і внутрішніх згинальних моментів
\[Pl \theta = K(\theta − \theta_o) \label{9.40}\]
Для геометрично досконалої колони\(\theta_o = 0\) та з Equation\ ref {9.40}
\[P = P_c = \frac{K}{l} \]
Рівняння\ ref {9.40} можна переписати через нормовану силу стиснення\(P/P_c\)
\[\frac{P}{P_c} \theta = \theta − \theta_o \]
Розв'язування цього рівняння для\(\theta\) врожайності
\[\theta = \theta_o \frac{1}{1 − \frac{P}{P_c}} \]
Графік наведеної вище функції показаний на малюнку (\(\PageIndex{2}\)). Термін\(1/(1 − \frac{P}{P_c} )\) називається коефіцієнтом збільшення. Він передбачає, наскільки збільшуються початкові недосконалості при заданій величині навантаження. При структурних недосконалостях відсутні первинні та вторинні шляхи рівноваги. Існує лише одна плавна крива відхилення навантаження, яка називається шлях рівноваги.
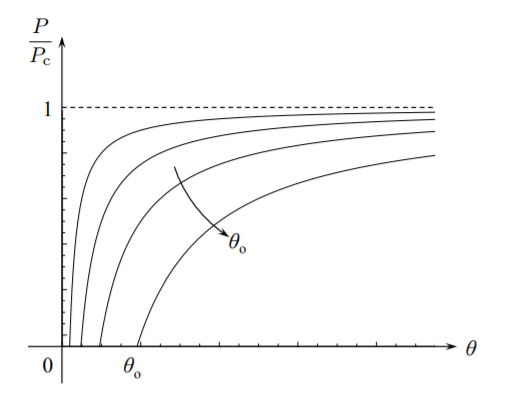
Цікаво відзначити, що при менших і менших початкових недосконалостях шляхи рівноваги наближаються до точки біфуркації, але ніколи не досягають її. Такий тип поведінки властивий всім недосконалим структурам.
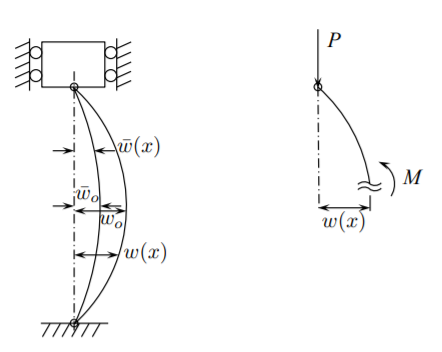
Як ще один приклад недосконалої конструкції розглянемо штифтовий пружний стовпчик. Вводяться такі позначення:
- \(\bar{w}(x)\)— форма початкової недосконалості
- \(\bar{w}_o\)— амплітуда початкової недосконалості
- \(w(x)\)- фактична форма з пряжками, виміряна з вертикального (ідеального) положення
- \(w_o\)— центральна амплітуда фактичного відхилення
Внутрішній згинальний момент дорівнює
\[M_{\text{int}} = EI \Delta\kappa = −EI(w^{\prime \prime} − \bar{w}^{\prime \prime}) \]
де\(\Delta\kappa\) - зміна кривизни від початкового вигнутого (недосконалого) стовпчика. Для просто підтримуваної колони кінцеві (реакційні) моменти дорівнюють нулю, тому зовнішній згинальний момент дорівнює
\[M_{\text{ext}} = P w \]
Прирівнюючи внутрішній і зовнішній згинальні моменти, отримуємо
\[EIw^{\prime \prime} + P w = EI\bar{w}(x) \label{9.46}\]
Це лінійне неоднорідне диференціальне рівняння другого порядку, де права сторона є відомою формою початкової недосконалості. Розв'язок цього рівняння існує через квадратури, але інтеграли важко оцінити для складних форм недосконалостей.
Розглянемо найпростіший випадок синусоїдальної форми недосконалостей. Можна показати, що розчин також\(w(x)\) синусоїдальної форми.
\[w(x) = w_o \sin \lambda x \label{9.47a}\]
\[\bar{w}(x) = \bar{w}_o \sin \lambda x \label{9.47b}\]
Кінематичними граничними умовами є
\[w(0) = w(l) = 0 \nonumber\]
що означає, що
\[\sin \lambda l = 0 \quad \rightarrow \quad \lambda l = n \pi \]
Підстановка рівнянь\ ref {9.47a} -\ ref {9.47b} у керівне рівняння\ ref {9.46}
\[−EI \lambda^2 (w_o − \bar{w}_o) \sin \lambda x − P w_o \sin \lambda x = 0 \]
який задовольняється, якщо
\[P w_o = EI(w_o − \bar{w}_o) \lambda^2 \label{9.50}\]
Для ідеального\(\bar{w}_o = 0\) стовпця і Equation\ ref {9.50} дає
\[(P_c − EI \lambda^2 )w_o = 0 \\ \text{or }P_c = EI\lambda^2 = \frac{n^2 \pi^2 EI}{l^2} \]
Для недосконалої колони
\[P w_o = P_c(w_o − \bar{w}_o) \]
або рішення для\(w_o\)
\[w_o = \bar{w}_o \frac{1}{1 − \frac{P}{P_c}} \]
Форма коефіцієнта збільшення ідентична тій, що виведена для окружної колони. Єдина відмінність полягає в тому, що безперервна колона має нескінченний режим вигину, де\(n = 1\) відповідає найнижчому навантаженню на вигин. Навантаження на вигин, що відповідає другому режиму вигину, в чотири рази більше тощо.
