Skip to main content
LibreTexts - Ukrayinska

8.5: Стабільність у напрузі

  1. Last updated
  2. Save as PDF
  • Page ID
    32952

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Для деяких матеріалів нестійкість в напрузі проявляється розвитком локальної шийки, рис. (\(\PageIndex{1}\)).

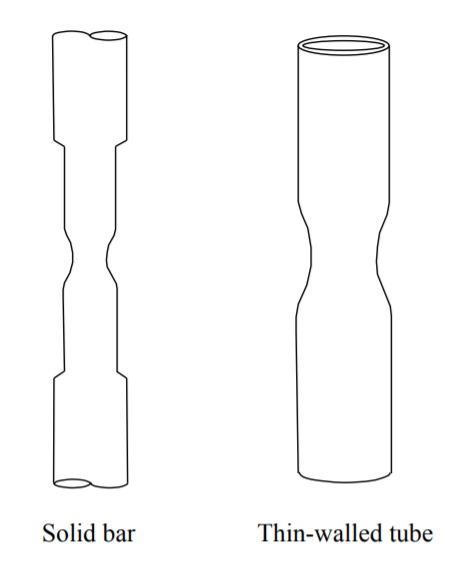
    8.5.1.png
    Малюнок\(\PageIndex{1}\): Шийка в суцільному перерізі бруса і тонкостінної труби під натягом.

    Розглянемо круглий пруток початкової площі поперечного перерізу, що\(A_o\) піддається зусиллям розтягування\(P\). Бар стає довшим і тому, що ефект Пуассона його поперечний переріз зменшується до значення струму\(A\). Цей аналіз справедливий для матеріалів, які є нестисливими, тобто не змінюють об'єм, а лише форму. Певні полімери, гума і метали (в пластиковому асортименті) є нестисливими.

    Обсяг нескінченно малої довжини\(l\) дорівнює

    \[ V = lA \]

    Приріст обсягу для нестисливого матеріалу повинен дорівнювати нулю

    \[\delta V = \delta (lA) = \delta lA + l \delta A = 0 \]

    Візьмемо логарифмічне визначення осьової деформації

    \[\epsilon = \ln \frac{l}{l_o} ; \quad \delta \epsilon = \frac{\delta l}{l} \]

    З перерахованих вище двох рівнянь

    \[\delta \epsilon = \frac{\delta l}{l}= − \frac{\delta A}{A} \]

    Інтеграція обох сторін

    \[\epsilon = − \ln A + C \nonumber\]

    В\(A = A_o\),\(\epsilon = 0\) так\(C = \ln A_o\).

    Тому виразом для осьової деформації стає

    \[\epsilon = \ln \frac{A_o}{A} = \ln \frac{l}{l_o} \]

    Зроблено висновок, що осьова деформація може бути визначена або вимірюванням зміни довжини, або зміною площі поперечного перерізу. Справжнє (Коші) напруга визначається як навантаження, розділене на поперечний переріз струму\(A\)

    \[\sigma = \frac{P}{A} \]

    Побудуємо загальну потенційну енергію і її першу варіацію

    \[\delta \prod = \int_{V} \sigma \delta \epsilon dv − P \delta u \label{9.60}\]

    Перед виникненням нестабільності деформація і напруга (одновісний натяг) рівномірні по перерізу бруса довжини\(l\)

    \[u = l \epsilon = l \ln \frac{A_o}{A} \label{9.61a}\]

    \[\delta u = −l \frac{\delta A}{A} \label{9.61b}\]

    Таким чином, з рівнянь\ ref {9.60} і\ ref {9.61a} -\ ref {9.61b}

    \[\delta \prod = \int_{V} \sigma \delta \epsilon dv + Pl \frac{\delta A}{A} \]

    Друга варіація загальної потенційної енергії -

    \[\delta^2 \prod = \int_{V} \delta \sigma \delta \epsilon dv − Pl \frac{\delta A \delta A}{A^2} \]

    Застосовуючи умову стійкості Trefftz,\(\delta^2 \prod = 0\) отримуємо

    \[lA \delta \sigma \delta \epsilon = Pl \delta \epsilon \delta \epsilon \]

    або

    \[\delta \sigma = \frac{P}{A} \delta \epsilon = \sigma \delta \epsilon \]

    і наостанок

    \[ \frac{\delta \sigma}{\delta \epsilon} = \sigma \label{9.66}\]

    Нестисливий стрижень втрачає стійкість у напрузі, коли локальна дотична до кривої напруження-деформації стає рівним значенню напруги в цій точці. Графічна інтерпретація показана на малюнку (\(\PageIndex{2}\)).

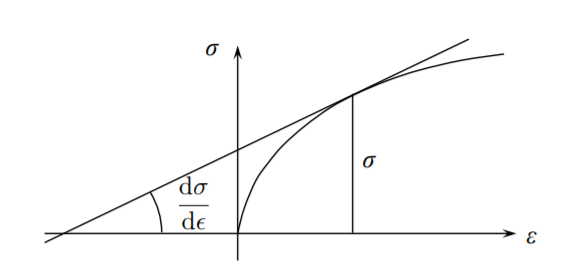
    8.5.2.png
    Малюнок\(\PageIndex{2}\): Побудова «Розглядач», який першим вивів рівняння\ ref {9.66}.

    При якому напруженні розвивається нестабільність для еластичного матеріалу? При одноосьовому напруженні

    \[\sigma = E\epsilon \]

    \[\frac{d\sigma}{d\epsilon} = E \]

    Рівняння\ ref {9.66} задовольняється, якщо\(\epsilon = 1\). Для металів така деформація не досяжна в еластичному діапазоні, оскільки вихід буде досягнутий при деформації\(\epsilon_y = \frac{\sigma_y}{E} \cong 10^{−3}\). Однак для гуми і подібних полімерних матеріалів модуль Юнга на чотири порядки менше, тому шийка є звичайним явищем. Виведення умови нестабільності\ ref {9.66} проводилося без будь-яких припущень про відношення напружено-деформованого матеріалу. Тому ця умова справедлива для еластичного, а також пластичного матеріалу. Це підводить нас до наступної теми, яка є пластиковим вигином колон.