4.1: Керуючі рівняння

Поки ми встановили три групи рівнянь, які повністю характеризують реакцію балок на різні типи навантаження. У главі 1 були встановлені відносини для обчислення деформацій з поля зміщення.

$$\epsilon(x, z) = \epsilon^{\circ}(x) + z\kappa$$

де

$$\epsilon^{\circ}(x) = \frac{du}{dx} + \frac{1}{2} \left( \frac{dw}{dx} \right)^2 \; , \; \kappa = −\frac{d^2w}{dx^2} \label{4.1.2}$$

Вищезазначені геометричні відносини є незалежними від рівноваги і застосовуються до будь-якого виду матеріалів.

Другий набір рівнянь, виведений у главі 2, є вимогою рівноваги

$$\frac{dV^*}{dx} + q(x) = 0 \quad − \quad \text{ force equilibrium}$$

$$\frac{dM}{dx} - V = 0 \quad − \quad \text{ moment equilibrium} \label{4.1.4}$$

де$V^* = V + N \frac{dw}{dx}$ ефективний зсув.

$$\frac{dN}{dx} = 0$$

Усуваючи$V$ та$V^*$ між вищезазначеними рівняннями, отримано рівняння рівноваги пучка (див. Рівняння (2.7.1))

$$\frac{d^2M}{dx^2} + N\frac{d^2w}{dx^2} + q = 0 \label{4.1.7}$$

Виведення рівноваги справедливо для всіх типів матеріалів. У теорії помірно великих прогинів рівновага пов'язана з кінематикою.

Третя група рівнянь визначає поведінку матеріалу і пов'язує узагальнені деформації з узагальненими силами.

$$N = EA\epsilon^{\circ} \label{4.1.8}$$

$$M = EI\kappa \label{4.1.9}$$

Незалежність геометрії та рівноваги від конституційного рівняння дозволяє розробити загальні рамки розв'язувача в кодах скінченних елементів. Установчі рівняння потім можуть бути додані як визначені користувачем підпрограми.

Розглянемо спочатку нескінченно малі деформації (малі обертання), для яких термін$\frac{1}{2} \left( \frac{dw}{dx} \right)^2$ зникає в Equation\ ref {4.1.2} та термін$\frac{d^2w}{dx^2} = 0$ у Equation\ ref {4.1.7}. Потім з рівнянь\ ref {4.1.2},\ ref {4.1.4} і\ ref {4.1.8} отримується

$$EA\frac{d^2u}{dx^2} = 0$$

Усуваючи кривизну і згинальні моменти між рівняннями\ ref {4.1.2},\ ref {4.1.7} і\ ref {4.1.9}, отримано рівняння прогину променя

$$EI\frac{d^4w}{dx^4} = q(x) \label{4.1.11}$$

Зосереджене навантаження$P$ можна розглядати як окремий випадок розподіленого навантаження$q(x) = P \delta(x − x_0)$, де$\delta$ є дельта-функція Дірака.

Розглянемо перше рівняння\ ref {4.1.4} для осьового зміщення. Граничні умови в$x$ -напрямку є

$$(N − \bar{N})\delta u = 0$$

Загальне рішення$u(x)$ для

$$\frac{du}{dx} = D_1 \; , \; u = D_1x + D_0 \label{4.1.13}$$

Є дві константи інтеграції, і потрібні дві граничні умови. Існує всього чотири комбінації граничних умов:

1. Балка обмежена від осьового руху, див. Рис.$\PageIndex{1}$

$$u(x = 0) = u(x = l) = 0$$

Це дає початок розв'язку двох алгебраїчних рівнянь

$$0 = D_0 + D_1 \cdot 0$$

$$0 = D_0 + D_1l$$

який дає$D_0 = D_1 = 0$ і$u(x) = 0$. Це банальний випадок, для якого також$N = EA\frac{du}{dx}$ зникає осьова сила.

Рисунок$\PageIndex{1}$: Три комбінації в площині граничних умов для$u(x)$.

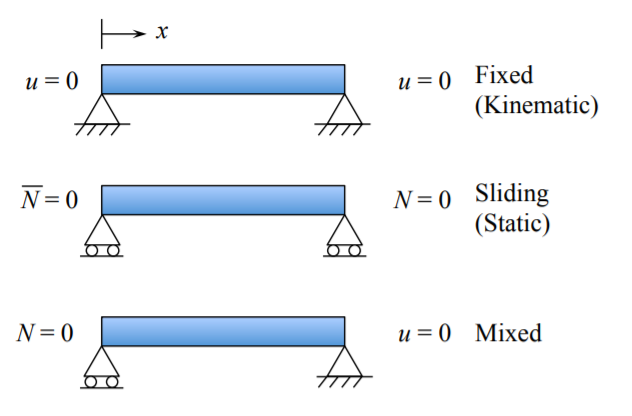
2. Балка допускається ковзати в$x$ -напрямку на обох кінцях.

$$\bar{N} = N = 0 \text{ at } x = 0 \text{ and } x = l$$

Осьова сила пропорційна$\frac{du}{dx}$. З Equation\ ref {4.1.13} ми бачимо, що градієнт$u$ дорівнює нулю вздовж всього променя. Отже, якщо$\bar{N} = 0$ або$\frac{du}{dx}$ зникає на одному кінці, скажімо$x = 0$,$D_1 = 0$ і автоматично$\bar{N} = 0$ задовольняється на іншому кінці,$x = l$. Константа інтеграції$D_0$ є невизначеною, що означає, що допускається трансляція твердого тіла всієї балки.

3. Щоб запобігти трансляції жорсткого тіла, один кінець балки, скажімо$x = 0$, повинен бути зафіксований проти руху в$x$ -напрямку. Таким чином

$$\bar{N} = 0 \text{ or } \frac{du}{dx} = 0 \quad \text{ at } \quad x = 0$$

$$u = 0 \quad \text{ at } \quad x = l$$

які є саме граничними умовами для третього випадку. З рівняння\ ref {4.1.13} отримуємо

$$D_1 = 0$$

$$D_1l + D_2 = 0 \rightarrow D_2 = 0$$

Тепер осьовий зсув зникає,$u(x) = 0$ але переклад жорсткого тіла усувається.

Для всіх перерахованих вище трьох випадків кінематичних статичних і змішаних граничних умов осьова сила дорівнювала нулю.

4. Якщо один кінець балки (бруса) навантажений заданою силою,$\bar{N}$ а інший закріплений, граничні умови (БК) складають

$$\begin{array}{lcl} N = -\bar{N} \; , \; EA\frac{du}{dx} = 0 & \text{ at } x = 0 \\ u = 0 & \text{ at } x = l \end {array}$$

$$D_1 = − \frac{\bar{N}}{EA} \; , \; D_2 = \frac{\bar{N}l}{EA}$$

і рішення

$$u(x) = \frac{\bar{N}}{EA} (l − x)$$

Набагато цікавіший випадок, коли нелінійний член зберігається в Equation\ ref {4.1.2}. Це буде розбиратися в розділі про помірно великому прогині балок.

Тепер звернемо увагу на рішення прогину балки, Equation\ ref {4.1.11}. Це лінійне неоднорідне рівняння четвертого порядку, яке вимагає чотирьох граничних умов. Існує чотири типи граничних умов, що визначаються

$$(M − \bar{M})\delta w^{\prime} = 0$$

$$(V − \bar{V}) \delta w = 0$$

Для ілюстрації вибираємо штифт БК для балки, завантаженої рівномірним подібним навантаженням$q$, Рисунок ($\PageIndex{2}$).

Малюнок$\PageIndex{2}$: Підтримка штифтів дозволяє обертати, але не для вертикального перекладу.

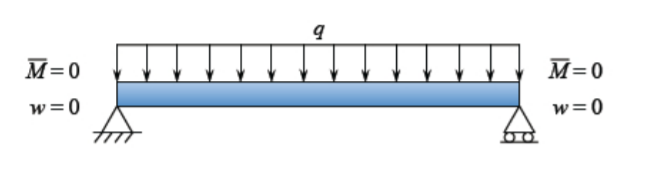
Згинальний момент пропорційний кривизні. Рівняння\ ref {4.1.11} потім піддається наступним граничним умовам:

$$w(x = 0) = w(x = l) = 0$$

$$\left. \frac{d^2w}{dx^2}\right|_{x=0} = \left. \frac{d^2w}{dx^2} \right|_{x=l} = 0$$

Давайте інтегруємо диференціальне рівняння чотири рази щодо$x$:

$$\begin{align} \frac{d^3w}{dx^3} &= \frac{qx}{EA} + C_1 \\[4pt] \frac{d^2w}{dx^2} &= \frac{qx^2}{EA2} + C_1x + C_2  \\[4pt] \frac{dw}{dx} &= \frac{qx^3}{EA6} + \frac{C_1x^2}{2} + C_2x + C_3  \\[4pt] w &= \frac{qx^4}{EA24} + \frac{C_1x^3}{6} + \frac{C_2x^2}{2} + C_3x + C_4 \end{align}$$

Підставляючи БК в загальні розв'язки, один отримує

$$0 = C_2$$

$$0 = \frac{ql^3}{2EA} + {C_1}l + C_2$$

$$0 = C_4$$

$$0 = \frac{ql^4}{24EA} + \frac{C_1l^3}{6} + \frac{C_2l^2}{2} + C_3l + C_4$$

Рішенням вищевказаної системи є

$$C_1 = −\frac{ql}{2}$$

$$C_2 = 0$$

$$C_3 = \frac{ql^3}{12}$$

$$C_4 = 0$$

Відношення навантаження-переміщення стає

$$w(x) = \frac{qx}{24EA}(l^3 - 2lx^2 + x^3) \label{4.1.40}$$

Диференціююче рівняння\ ref {4.1.40} двічі, вираз для згинального моменту дорівнює

$$M(x) = \frac{qx}{2} (l − x)$$

і диференціюючи знову, сила зсуву стає

$$V(x) = \frac{dM}{dx} = \frac{q}{2} (l − 2x)$$

Графіки нормованих згинальних моментів і сил зсуву наведені на малюнку ($\PageIndex{3}$).

Малюнок$\PageIndex{3}$: Параболічний розподіл згинального моменту і лінійна зміна сили зсуву.

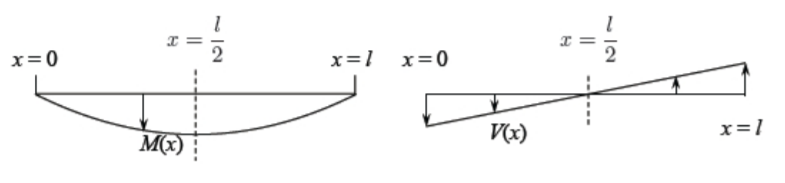
Зсувна сила$V = EI\frac{d^3w}{dx^3}$, як видно, зникає в середині прольоту балки. Також ухил$\frac{dw}{dx}$ дорівнює нулю в цьому місці. Доведено, що на площині симетрії

$$V (x = \frac{l}{2} ) = 0 \label{4.1.43}$$

$$\left. \frac{dw}{dx}\right|_{x= \frac{l}{2}} = 0 \label{4.1.44}$$

І навпаки, якщо задача симетрична, то рівняння\ ref {4.1.43} -\ ref {4.1.44} повинні триматися на площині симетрії. В якості альтернативної формулювання можна розглянути половину пучка з симетрією до н.е.

Чи можете ви вирішити вищезазначену задачу і порівняти її з розв'язком штифтового пучка, Equation\ ref {4.1.40}?

Малюнок$\PageIndex{4}$: Проста опорна пластина з граничними умовами симетрії.

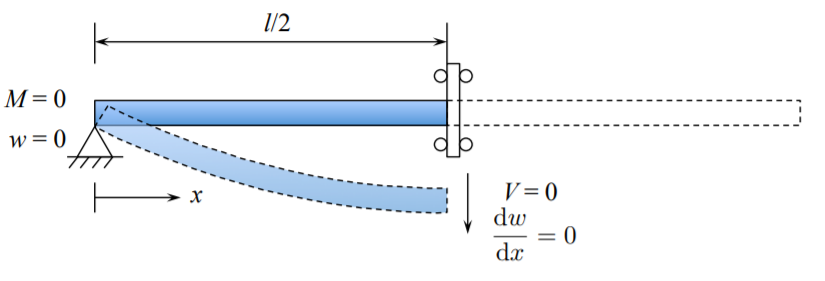
Слід зазначити, що опорна балка з штифтовим штифтом є статично визначальною конструкцією. Тому розподіл зсувних сил і згинальних моментів можна визначити лише з рівняння рівноваги. Чи можете ви це зробити і правильно отримати знаки?

Мета глави 4 - представити властивості керівних рівнянь та розв'язків. Зацікавлені студенти посилаються на кінцеву главу множин задач, де розглянуто багато пучків з різним навантаженням та БК. Також рекомендований довідник і монографії представляють рішення деяких поширених проблем променя.