4.3: Статично визначені промені

Last updated
Save as PDF

Page ID: 32971

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Балка, для якої розподіл згинальних моментів і сил зсуву можна визначити лише з рівноваги, називають статично визначеними балками. Для таких балок\(M(x)\) і\(V (x)\) відомі і визначення прогину балки буде набагато простіше завданням. Об'єднання рівняння (4.1.9) з рівнянням (4.1.2) закінчується наступним лінійним диференціальним рівнянням другого порядку

\[−EI \frac{d^2w}{dx^2} = M(x) \label{4.3.1}\]

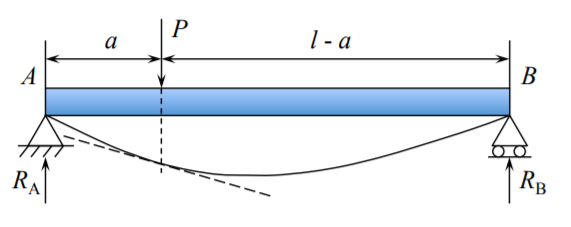
Згинальний момент, який сам по собі повинен задовольняти диференціальному рівнянню другого порядку, Рівняння (4.1.7) тепер має підкорятися двом граничним умовам напружень на кінцях балки. Статичні граничні умови вказані на малюнку (\(\PageIndex{1}\)) для штифтової опори та консольної балки.

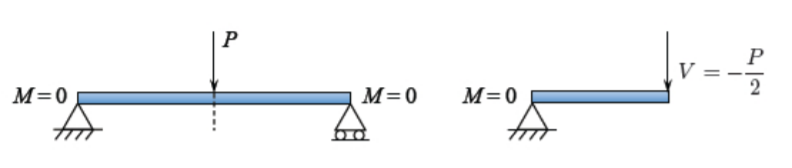
4.3.1.png — Малюнок\(\PageIndex{1}\): Статичні граничні умови для повної і половини балки.

Визначення діаграм згинального моменту і сили зсуву є предметом елементарних курсів статики, і загальна процедура тут не пояснюється. У випадку з просто спирається балкою з точковим навантаженням на середині прольоту згинальні моменти

\[M(x) = \begin{cases} \frac{P x}{2} , & 0 < x < \frac{l}{2} \\ \frac{P(l − x)}{2} , & \frac{l}{2} < x < l \end{cases} \label{4.3.2}\]

Згинальний момент зникає при\(x = 0\) і\(x = l\).

Відповідна сила\(V = \frac{dM}{dx}\) зсуву

\[V(x) = \begin{cases} \frac{P}{2} , & 0 < x < \frac{l}{2} \\ - \frac{P}{2} , & \frac{l}{2} < x < l \end{cases} \]

У центрі променя

\[[V ] = \frac{P}{2} − \left[ − \frac{P}{2} \right] = P\]

Через розрив сили зсуву в центрі променя, рішення буде шукатися для половини балки. Кожна половина балки несе половину навантаження. Показано, що розподіл згинального моменту задовольняє двом граничним умовам атласу. Тому диференціальне рівняння\ ref {4.3.2} піддається лише двом кінематичним граничним умовам

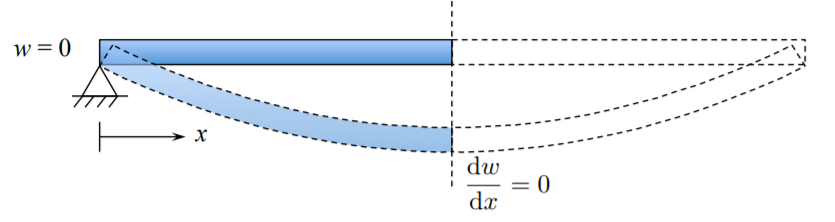
4.3.2.png — Малюнок\(\PageIndex{2}\): Гранична умова симетрії.

Інтеграція рівняння\ ref {4.3.1} двічі отримує один

\[−EIw = \frac{P x^3}{12} + C_1x + C_2\]

Дві інтеграційні константи, що визначаються з граничних умов\(w(0) = 0, \quad \left. \frac{dw}{dx} \right|_{ x= \frac{l}{h}} = 0\),

\[C_1 = −\frac{Pl^2}{16}, \quad C_2 = 0\]

а лінія прогину балки задається

\[w(x) = \frac{Px}{48EI} (3l^2 - 4x^2) \quad 0 < x < \frac{l}{2}\]

Друга половина променя - дзеркальне відображення, по симетрії. Зокрема, центральний прогин\(w_o = w(x = \frac{l}{2})\) виражається всіма вхідними параметрами балки як

\[w_o = \frac{Pl^3}{48EI}\]

Буде корисно запам'ятати вищевказану формулу до кінця свого професійного життя.

Підводячи підсумок, визначення прогинів статично визначених балок набагато простіше, ніж його статично невизначені аналоги. Керуюче рівняння другого порядку, а для симетричних задач існує лише дві константи інтеграції.

4.3.3.png — Малюнок\(\PageIndex{3}\): Балка під навантаженням поза центром точки.