Skip to main content
LibreTexts - Ukrayinska

8.1: Оцінка

  1. Last updated
  2. Save as PDF
  • Page ID
    30057

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

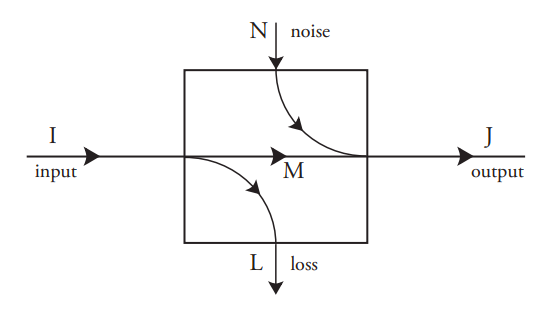
    Часто необхідно визначити вхідну подію, коли спостерігалася лише вихідна подія. Це стосується систем зв'язку, в яких мета полягає в тому, щоб зробити висновок символу, що випромінюється джерелом, щоб його можна було відтворити на виході. Це також стосується систем пам'яті, в яких метою є відтворення вихідного бітового шаблону без помилок.

    В принципі, ця оцінка проста, якщо відомий розподіл вхідних ймовірностей\(p(A_i)\) та умовні вихідні ймовірності, обумовлені на вхідних подіях.\(p(B_j \;|\; A_i) = c_{ji}\) Ці «вперед» умовні ймовірності\(c_{ji}\) утворюють матрицю з такою кількістю рядків, скільки є вихідні події, і стільки стовпців, скільки є вхідні події. Вони є властивістю процесу, і не залежать від вхідних ймовірностей\(p(A_i)\).

    Безумовна\(p(B_j)\) ймовірність кожної\(B_j\) вихідної події

    \(p(B_j) = \displaystyle \sum_{i} c_{ji}p(A_i)\tag{8.1}\)

    Знімок екрана 2021-05-19 о 11.14.10 PM.png
    Малюнок 8.1: Інформаційний потік в дискретному процесі без пам'яті

    а спільна ймовірність кожного входу з кожним виходом\(p(A_i, B_j)\) і зворотними умовними ймовірностями\(p(A_i \;|\; B_j)\) можна знайти за допомогою теореми Байєса:

    \ begin {вирівнювати*}
    p (A_ {i}, B_ {j}) &=p (B_ {j}) p (A_ {i}\; |\; B_ {j})\\
    &= p (A_ {i}) p (B_ {j}\; |\; A_ {i})\ тег {8.2}\
    &= p (A_ {i}) c_ {ji}
    \ end {вирівнювати*}

    Тепер припустимо, що певна вихідна подія\(B_j\) спостерігалася. Вхідну подію, яка «викликала» цей вихід, може бути оцінена лише за ступенем розподілу ймовірностей по вхідних подіях. Для кожної\(A_i\) вхідної події ймовірність того, що це був вхід, просто зворотна\(p(A_i \;|\; B_j)\) умовна ймовірність для конкретної вихідної події\(B_j\), яку можна записати за допомогою Equation 8.2 як

    \(p(A_i \;|\; B_j) = \dfrac{p(A_i)c_{ji}}{p(B_j)} \tag{8.3}\)

    Якщо процес не має втрат (\(L\)= 0), то для кожного\(j\) рівно одне з вхідних подій\(A_i\) має ненульову ймовірність, а отже його ймовірність\(p(A_i \;|\; B_j)\) дорівнює 1. У більш загальному випадку, при ненульових втратах, оцінка складається з уточнення набору вхідних ймовірностей, щоб вони узгоджувалися з відомим виходом. Зауважте, що цей підхід працює, лише якщо відомий вихідний розподіл ймовірностей. Все, що він робить, - це вдосконалити цей розподіл у світлі нових знань, а саме спостережуваного виходу.

    Можна подумати, що новий розподіл вхідних ймовірностей матиме меншу невизначеність, ніж у вихідному розподілі. Чи завжди це правда?

    Невизначеність розподілу ймовірностей - це, звичайно, його ентропія, як визначено раніше. Невизначеність (про вхідну подію) перед відомою вихідною подією

    \(U_{\text{before}} = \displaystyle \sum_{i} p(A_i) \log_2 \Big(\dfrac{1}{p(A_i)}\Big) \tag{8.4}\)

    Залишкова невизначеність, після того, як відомо якась конкретна вихідна подія, є

    \(U_{\text{after}}(B_j) = \displaystyle \sum_{i} p(A_i \;|\; B_j) \log_2 \Big(\dfrac{1}{p(A_i \;|\; B_j)}\Big) \tag{8.5}\)

    Питання, тоді в тому, чи є\(U_{\text{after}}(B_j) ≤ U_{\text{before}}\). Відповідь часто, але не завжди, так. Однак неважко довести, що середня (за всіма вихідними станами) залишкової невизначеності менше початкової невизначеності:

    \(\displaystyle \sum_{j} p(B_j)U_{\text{after}}(B_j) ≤ U_{\text{before}} \tag{8.6}\)

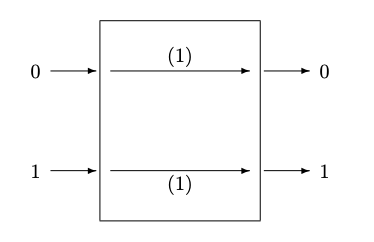
    Знімок екрана 2021-05-19 о 11.27.02 PM.png
    (а)
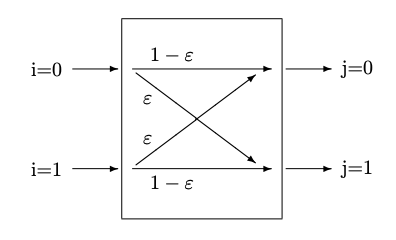
    Знімок екрана 2021-05-19 о 11.27.20 PM.png
    (б)

    Малюнок 8.2: (a) Двійковий канал без шуму (b) Симетричний двійковий канал, з помилками

    На словах це твердження говорить про те, що в середньому наша невизначеність щодо вхідного стану ніколи не збільшується, дізнавшись щось про вихідний стан. Іншими словами, в середньому ця методика висновку допомагає нам отримати кращу оцінку вхідного стану.

    Два з наступних прикладів будуть продовжені в наступних розділах, включаючи наступну главу про Принцип максимальної ентропії - симетричний двійковий канал і Бергера Бургера.