8.5: Термоелектричні ефекти

Last updated
Save as PDF

Page ID: 29561

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Три пов'язані ефекти

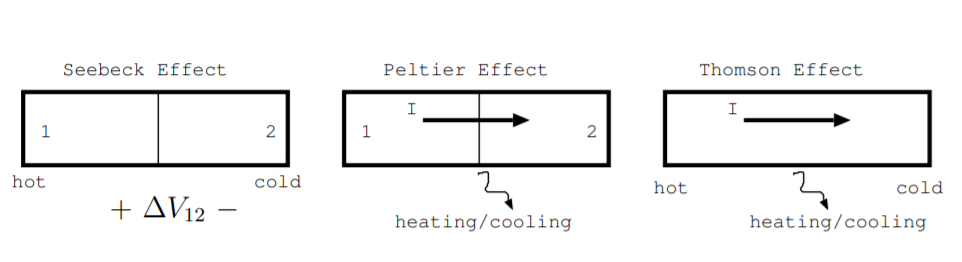
8.5.1.PNG — Малюнок$\PageIndex{1}$: Ефект Зеєбека, ефект Пельтьє та ефект Томсона.

У 1800-х роках експериментально спостерігалося три ефекти. Спочатку було неочевидно, що ці експерименти були пов'язані між собою, але незабаром вони виявилися трьома аспектами одного і того ж явища [5, с. 113].

Перший ефект, який зараз називають ефектом Зеєбека, був відкритий в 1821 році Томасом Зеебеком [5, с. 113]. Спостерігається в місці з'єднання двох різних металів або напівпровідників. Як обговорювалося в розділі 6.4, переходи також використовуються для виготовлення фотоелектричних пристроїв, світлодіодів та напівпровідникових лазерів. Коли різні сторони переходу утримуються при різних температурах, на переході розвивається напруга. Коефіцієнт$$$ Зеєбека в одиницях$\frac{V}{K}$ визначається як відношення цієї напруги до різниці температур. Більш конкретно розглянемо стик, де одна сторона утримується при більш гарячій температурі, ніж інша, як показано в лівій частині рис. $\PageIndex{1}$. Різниця між коефіцієнтом Зеєбека в матеріалі один$$_1$ і коефіцієнтом Зеєбека в матеріалі два$$_2$ задається виміряною напругою на переході,$\Delta V_{12}$ поділеним на різницю температур між матеріалами$\Delta T_{12}$ [110, стор. 24].

\[$_1 - $_2 = \frac{\Delta V_{12}}{\Delta T_{12}} \nonumber \]

Різниця між коефіцієнтами Зеєбека може бути позитивною або негативною, оскільки і різниця температур, і вимірювана напруга можуть бути позитивними або негативними. Однак для будь-якого даного матеріалу коефіцієнт Зеєбека є позитивним. Щоб знайти коефіцієнт Зеєбека для невідомого матеріалу, сформуйте стик між цим матеріалом і матеріалом з відомим коефіцієнтом Зеєбека, нагрійте один кінець переходу гаряче, ніж інший, і виміряйте встановлену напругу. Для більшості матеріалів коефіцієнт Зеебека менше$1 \frac{\mu V}{K}$. Деякі з найбільших значень коефіцієнта Зеебека знаходяться в матеріалах, що містять телур. Наприклад, (Bi$_{0.7}$ Sb$_{0.3})_2$ Te$_3$ має,$$ \approx 230 \frac{\mu V}{K} $ а PbTe має$$ \approx 400 \frac{\mu V}{K}$ [3].

Щоб зрозуміти фізику, що стоїть за ефектом Зеєбека, розглянемо потік зарядів через цей діодно-подібний пристрій. У металах валентні електрони є носіями заряду, а в напівпровідниках носіями заряду є і валентні електрони, і дірки. Ці носії заряду дифундують від гарячої до холодної сторони переходу. Розглянемо стик двох металів без чистого заряду з обох сторін спочатку. Якщо електрон рухається з гарячої сторони в холодну сторону, то гаряча сторона тоді матиме чистий позитивний заряд, а холодна сторона матиме чистий негативний заряд. Цей рух зарядів встановлює електричне поле і, отже, напруга.

Якщо ми дозволимо зразку досягти рівноважної температури, напруга не вимірюватиметься. Напруга вимірюється тільки в той час, коли носії заряду розсіялися від одного матеріалу до іншого, але коли матеріал не досяг рівномірної температури. Таким чином, щоб матеріал мав великий термоелектричний ефект, він повинен мати велику електропровідність і малу теплопровідність. Термоелектричні пристрої, як правило, виготовляються з металів або напівметалів, оскільки ці матеріали задовольняють цій умові.

Другий ефект був відкритий Жаном Пельтьє в 1834 році [5, с. 113]. Ефект Пельтьє також спостерігається в місці з'єднання двох різних металів, напівметалів або напівпровідників. Вона проілюстрована в середній частині рис. $\PageIndex{1}$. При подачі струму,$I$ в амперах, через перехід відбувається передача тепла. Цей ефект виникає через те, що заряди від подається струму протікають через різні матеріали з різною теплопровідністю з різних сторін переходу. Ефект кількісно визначається коефіцієнтом Пельтьє для переходу$\displaystyle \prod_{12}$, або коефіцієнтами Пельтьє для матеріалів, що утворюють стик,$\displaystyle \prod_1$ і$\displaystyle \prod_2$. Більш конкретно, коефіцієнт Пельтьє визначається як

\[\prod_{12} = \prod_1 - \prod_2 = \frac{ \left( \frac{d\mathbb{Q}}{dt} \right) }{I} \nonumber \]

в одиницях вольт [110, стор. 24]. Термін$\frac{d\mathbb{Q}}{dt}$ являє собою швидкість передачі тепла$\frac{J}{s}$, і вона може бути позитивною або негативною, оскільки теплопровідність в першому матеріалі може бути вище або нижче, ніж у другому матеріалі. Коефіцієнт Зеебека і коефіцієнт Пельтьє пов'язані

\[\prod_1 - \prod_2 = ($_1 - $_2)T. \nonumber \]

PbTe - матеріал з відносно високим коефіцієнтом Зеєбека. При кімнатній температурі він має коефіцієнти$$ = 400 \frac{\mu V}{K}$ і

\[\prod = 400 \frac{\mu V}{K} \cdot 300K = 0.12V. \nonumber \]

Третій ефект вперше був відкритий Вільямом Томсоном в 1860-х роках [3]. Томсон також вивів зв'язок між цими трьома ефектами. Вона проілюстрована на правій частині рис. $\PageIndex{1}$. Коли струм проходить через однорідний шматок матеріалу, який має температурний градієнт, відбудеться нагрівання або охолодження, і цей результат відомий як ефект Томсона [3, с. 148] [110, с. 24] [5, с. 115]. Щоб спостерігати за цим ефектом, застосуйте градієнт температури на шматок металу або напівпровідника, а також подайте струм по довжині матеріалу. Нагрівання або охолодження можна виміряти, і цей ефект описується іншим коефіцієнтом. Коефіцієнт Томсона$\tau$ також має одиниці$\frac{V}{K}$. Він визначається як швидкість теплоти, що утворюється над добутком струму і різниці температур.

\[ \tau = \frac {\frac {d\mathbb{Q}} {dt}} {I(T_h-T_c)} \nonumber \]

Коефіцієнти Томсона і Зеебека для одного матеріалу пов'язані

\[\int_{0}^{T} \frac{\tau}{T^{\prime}} d T^{\prime}=$ \nonumber \]

де інтеграл - над температурою [110, стор. 24].

Ці ефекти працюють в обох напрямках. Ми можемо використовувати ефект Пельтьє, наприклад, щоб зробити або нагрівальний, або охолоджуючий пристрій. Ми можемо подавати струм через перехід для отримання перепаду температур, або ми можемо поставити різницю температур для генерації струму. Всі три ефекти пов'язані з тим, що коли електропровідність більше теплопровідності, енергія може перетворюватися між перепадом температур і електрикою. Крім того, матеріали з низькою електропровідністю і високою теплопровідністю також використовуються для виготовлення пристроїв перетворення енергії. Компоненти двигунів і генераторів часто виготовляються з шарів металу і діелектриків з цими властивостями [111, гл. 8].

Електропровідність

Електропровідність$\sigma$, в одиницях$\frac{1}{\Omega \cdot m}$, - це міра здатності зарядів протікати через матеріал. Питомий опір - зворотна електропровідність,$\rho = \frac{1}{\sigma}$. Приклади значень електропровідності наведені в таблиці 8.2.1, наведеної в розділі 8.2. Для вимірювання цих величин потрібно мало інструментів. Омметр може бути використаний для пошуку опору$R$, в Омах, зразка з відомою довжиною$l$ і площею поперечного перерізу$A$. Провідність може бути розрахована безпосередньо,

\[\sigma = \frac{l}{AR}. \nonumber \]

Електропровідність - добуток кількості зарядів, що протікають, і їх рухливості. Для провідників валентні електрони є носіями заряду, які протікають, тому провідність може бути виражена як [9, с. 84]

\[\sigma = nq\mu_n. \nonumber \]

У цьому виразі n - концентрація валентних електронів в одиницях електронів$m^3$, і вона була введена в п. 5.1. Величина заряду електрона дорівнює$q = 1.6 \cdot 10^{-19} C$. Рухливість електронів - це легкість$\mu_n$, з якою носії заряду дрейфують у матеріалі, і він має одиниці$\frac{m^2}{V \cdot s}$. За визначенням рухливість - це відношення середньої швидкості дрейфу електронів до прикладеного електричного поля в$\frac{V}{m}$ [9, с. 84].

\[\mu_n = \frac{\text{-avg drift velocity of electrons}}{\left|\overrightarrow{E}\right|} \nonumber \]

Для напівпровідників як електрони, так і дірки виступають носіями заряду, і обидва сприяють провідності,

\[\sigma = q(n\mu_n + p\mu_p) \nonumber \]

де$\mu_p$ - рухливість отворів, і$p$ - концентрація отворів.

Щоб зрозуміти, які матеріали мають велику електропровідність, а значить, і зробити хороші термоелектричні пристрої, нам потрібно враховувати концентрації заряду$n$ і$p$. Провідники та напівпровідники мають заряди, які можуть рухатися через матеріал, тоді як ізолятори - ні. При цьому провідники і напівпровідники мають велику електропровідність і використовуються для виготовлення термоелектричних приладів. Крім того, легований напівпровідник має більше носіїв заряду, ніж нелегований, який також називають внутрішнім напівпровідником. Так, леговані напівпровідники зазвичай мають більш високу електропровідність, ніж нелеговані напівпровідники з того ж матеріалу [110].

$\sigma$Електропровідність пропорційна електронній і дірковій рухливості$\mu_p$,$\mu_n$ причому, і рухливість є сильною функцією температури [9]. З цієї причини електропровідність є функцією температури. При низькій температурі рухливість обмежується розсіюванням домішок, тоді як при високих температурах вони обмежені фононним розсіюванням. При деякій проміжній температурі рухливість і провідність максимальні, і цей пік припадає на різні температури для різних матеріалів. Рухливість також залежить від того, чи є матеріал кристалічним або аморфним, і від ступеня кристалічності. Рухливість та електропровідність зазвичай вищі у кристалах, ніж у окулярах, оскільки заряди частіше розсіюються в аморфних матеріалах.

Теплопровідність

8.5.2.png — Малюнок$\PageIndex{2}$: Компоненти, що використовуються для вимірювання теплопровідності.

Теплопровідність$\kappa$ - це міра здатності тепла протікати через матеріал, і вона має одиниці$\frac{W}{m \cdot K}$ [109, с. 793]. Приклади значень теплопровідності наведені в таблиці 8.2.1, наведеної в розділі 8.2. Розуміння теплопровідності ускладнюється тим, що за провідність тепла відповідає ряд механізмів. Тепло може транспортуватися фононами, фотонами, електронами або іншими механізмами, і кожен механізм залежить від температури і властивостей матеріалу. Хороші термоелектричні прилади мають невелику теплопровідність. Часто метали мають велику теплопровідність, а ізолятори мають малу теплопровідність.

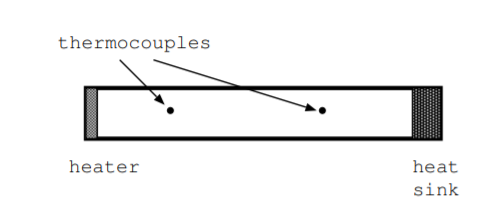
Апарат для вимірювання теплопровідності складається з нагрівача, радіатора і ряду термопар [110] [112]. Щоб виміряти теплопровідність експериментальним шляхом, почніть з бруска матеріалу з відомою площею поперечного перерізу$A$. Нагрійте один кінець планки по відношенню до іншого, дочекайтеся стійкого теплового стану, і виміряйте температуру на кожному кінці планки. Далі обчислюємо температурний градієнт$\frac{dT}{dx}$ в одиницях$\text{K}{m}$ по довжині бруса. Також виміряйте швидкість, яку тепло подається на планку$\frac{d\mathbb{Q}}{dt}$, в одиницях$\frac{J}{s}$. За визначенням теплопровідність - це співвідношення

\[\kappa = \frac{\text{(power dissipated in heater)(distance between thermocouples)}}{\text{(cross sectional area)(change in temp)}} \nonumber \]

[109, с. 49]. Теплопровідність можна обчислити по

\[\kappa = \frac{- \left( \frac{d\mathbb{Q}}{dt} \right)}{A \left( \frac{dT}{dx} \right)}. \nonumber \]

Ця методика добре працює при низьких і помірних температурах і матеріалах з високою теплопровідністю. Існують інші методи вимірювання теплопровідності і вигідні для різних діапазонів температур або провідності.

Інший спосіб зрозуміти теплопровідність - це думати про неї як про добуток кількості тепла, що транспортується деякими частинками, що перевищує швидкість цієї частинки. Ця точка зору стосується того, чи беруть участь фактичні частинки у транспорті тепла. Більш конкретно теплопровідність задається

\[\kappa = C_v|\overrightarrow{v}|l \nonumber \]

Символ$C_v$ представляє питому теплоту при постійному обсязі в$\frac{J}{g \cdot K}$, а символ$|\overrightarrow{v}|$ представляє величину транспортної швидкості в$\frac{m}{s}$. Довжина розсіювання представлена$l$ в$m$.

Незалежно від того, чи електрони, фонони чи щось інше транспортують тепло через матеріал, здатність цього тепла потрапляти з одного кінця в інший без розсіювання або блокування впливає на теплопровідність. Так, кристали зазвичай мають більш високу теплопровідність, ніж аморфні матеріали [113]. Теплопровідність кристала можна знизити, піддаючи матеріал випромінюванню, яке руйнує кристалічність і збільшує ймовірність того, що теплоносій буде розсіяний [110]. Для окулярів довжина розсіювання приблизно дорівнює міжатомному інтервалу [112]. Також теплопровідність стекол менш залежна від температури, ніж кристалів, оскільки високі температури спотворюють ідеальну кристалічність, тим самим знижуючи теплопровідність кристалів, але не стекол [113].

Всі фактори, що сприяють$C_v$$|\overrightarrow{v}|$, і довжина$l$ розсіювання залежать від температури, тому теплопровідність є функцією температури. Температурна залежність факторів розглядається в довіднику [110]. Теплопровідність, як і електропровідність, низька при низьких температурах, потім підвищується до максимуму, перш ніж знову знижуватися при більш високих температурах [112].

Фігура заслуг

Цифра заслуг термоелектричного пристрою$Z$, є єдиною мірою, яка підсумовує, наскільки хороший матеріал для виготовлення термоелектричних пристроїв. Він визначається як

\[Z = \frac{$^2 \sigma}{\kappa}, \nonumber \]

і він має одиниці$K^{-1}$. Це залежить від коефіцієнта Зеєбека$$$, електропровідності$\sigma$ та теплопровідності$\kappa$. Велике значення$Z$ говорить про те, що матеріал є хорошим вибором для використання в будівництві термоелектричного приладу.

Цифра заслуг залежить від температури, оскільки параметри$$$$\sigma$, і$\kappa$ є сильними функціями температури. Таким чином, найкращий вибір матеріалу для термоелектричного пристрою, що працює поблизу кімнатної температури, може бути не найкращим вибором для пристрою, що працює при інших температурах. Іноді$ZT$ використовується як міра, а не просто$Z$ для обліку температурної залежності.

Цифра заслуг не включає всі фактори, пов'язані з температурою, які слід враховувати при виборі матеріалів для термоелектричних пристроїв. Температура плавлення також важлива. Термоелектричний пристрій перетворює більше енергії, коли через пристрій розміщується більша різниця температур. Коефіцієнт Зеебека обернено пропорційний перепаду температур,$$ = \frac{\Delta V}{\Delta T}$. Однак занадто великий перепад температур розплавить гарячий кінець пристрою, і різні матеріали можуть мати дуже різні температури плавлення. Наприклад, телурид свинцю PbTe плавиться at$924 ^{\circ}C$, а Bi$_2$ Te$_3$ плавиться при$580 ^{\circ}C$ [114, с. 4-52, 4-71].

Цифра заслуг також залежить від рівня легування, оскільки електропровідність прямо пропорційна концентрації заряду$n$ і$p$ [110]. Таким чином, термоелектричний прилад, виготовлений з легованого напівпровідника, має більш високу електропровідність і термоелектричний ККД, ніж прилад, виготовлений з нелегованого напівпровідника з того ж матеріалу. Коефіцієнт Зеєбека також залежить від рівня допінгу, але не так сильно [110]. Теплопровідність не є сильною функцією концентрацій заряду$n$ і$p$ [110]. Так, термоелектричні матеріали часто виготовляють з сильно легованих напівпровідників або з провідників.

Цифра заслуг також залежить від ступеня кристалічності. Як правило, і електропровідність, і теплопровідність набагато вище у кристалів, ніж у стеклах, оскільки заряд і теплоносії рідше розсіюються, коли вони подорожують крізь кристали, ніж скла [113]. Оскільки впливають як електрична, так і теплопровідність, вплив ступеня кристалічності на фігуру заслуг може бути ускладненим.

Термоелектричні пристрої, як правило, виготовляються з з'єднань двох різних металів або напівпровідників. По суті, термоелектричний прилад - це діод. Загальні використовувані матеріали включають телурид вісмуту, телурид свинцю та телурид сурми, всі з яких є напівметалами. Bi, Sb і Pb всі розташовані один біля одного на таблиці Менделєєва. Інші матеріали, вивчені для використання в термоелектричних пристроях, включають [110], BiSete, LiMnO, LiCoO, LiCoO, LiniO, PbS та ZnSb. Ці матеріали є або напівпровідниками з невеликим зазором, або напівметалами. У напівпровідникових матеріалах з малими енергетичними зазорами відношення електропровідності до теплопровідності велике. Однак цей факт повинен бути збалансований з тим, що напівпровідники з меншим зазором, як правило, мають більш низькі температури плавлення, ніж напівпровідники з більшим зазором [110, гл. 1].

Останнім часом шаруваті матеріали і надрешітки розглядаються як матеріали для термоелектричних приладів [115] [116]. Шари можуть бути пристосовані, щоб по-різному впливати на теплові та електричні властивості і можуть діяти як фільтр для вибору різних механізмів провідності. Розуміння механізмів провідності є необхідною умовою для розуміння таких більш складних структур.