5.1: Фізика ефекту Холла

Пристрої з ефектом Холла - це пристрої прямого перетворення енергії, які перетворюють енергію з магнітного поля в електрику. Фізика, що стоїть за цими пристроями, описується рівнянням сили Лоренца. Ця дискусія слідує за посиланнями [3] і [9]. Якщо помістити заряд у зовнішнє електричне поле, він буде відчувати силу, паралельну прикладеному електричному полю. Якщо помістити рухомий заряд у зовнішнє магнітне поле, він буде відчувати силу, перпендикулярну прикладеному магнітному полю. Рівняння сили Лоренца\[\overrightarrow{F} = Q\left(\overrightarrow{E} + \overrightarrow{v} \times \overrightarrow{B} \right) \nonumber \]

описує сили на рухомий заряд за рахунок зовнішніх електричних і магнітних полів. У наведеному вище рівнянні\(\overrightarrow{F}\) представляє силу в ньютонах на заряді, що рухається зі швидкістю\(\overrightarrow{v}\) в одиницях\(\frac{m}{s}\). Величина\(\overrightarrow{E}\) представляє напруженість електричного поля в одиницях\(\frac{V}{m}\) і\(\overrightarrow{B}\) являє собою щільність магнітного потоку в одиницях\(\frac{Wb}{m^2}\). Заряд в кулоні позначається символом\(Q\). Зверніть увагу, що сила на заряді за рахунок електричного поля вказує в тому ж напрямку, що і електричне поле, в той час як сила на заряді за рахунок магнітного поля вказує перпендикулярно як швидкості заряду, так і напрямку магнітного поля.

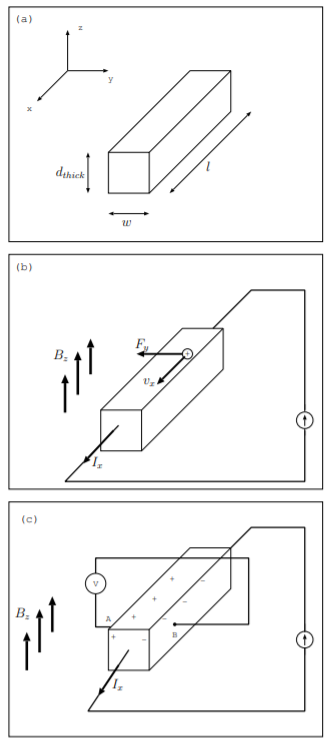
Ефект Холла виникає як в провідниках, так і в напівпровідниках. У провідниках електрони є носіями заряду, що відповідають за ефект, тоді як в напівпровідниках як електрони, так і дірки є носіями заряду, відповідальними за ефект [9]. Дірка - це відсутність електрона. Розглянемо шматок напівпровідника, орієнтований так, як показано на рис. \(\PageIndex{1}\)а Припустимо, що довжина задається\(l\), ширина вказана\(w\), а товщина задається\(d_{thick}\). Для типового пристрою з ефектом Холла ці розміри можуть бути в міліметровому діапазоні. Крім того, припустимо, що напівпровідник p-типу з концентрацією отворів\(p\) в одиницях\(m^{-3}\). Концентрація заряду являє собою чисту або надлишкову щільність заряду вище нейтрального матеріалу. Матеріали з чистим негативним зарядом, надлишковими валентними електронами, матимуть позитивне значення для концентрації електронів\(n\) і називаються n-типом. Матеріали з чистим позитивним зарядом, надлишком отворів, матимуть позитивне значення для концентрації отворів,\(p\) що представляє щільність отворів у матеріалі і називаються p-типом. Загальна щільність заряду\(n\) пов'язана з\(p\)\[\rho_{ch} = -qn + qp \nonumber \]

де\(q\) - величина заряду електрона.

Припустимо, що напівпровідник поміщений у зовнішнє магнітне поле, орієнтоване в\(\hat{a}_z\) напрямку, з щільністю магнітного потоку\[\overrightarrow{B} = B_z\hat{a}_z. \nonumber \]

Також припустимо, що струм подається через напівпровідник в\(\hat{a}_x\) напрямку. Позитивні носії заряду в напівпровіднику, дірки, рухаються зі швидкістю,\(\overrightarrow{v} = v_x\hat{a}_x\) оскільки струм - це потік заряду в одиницю часу. Ці заходи проілюстровані на рис. \(\PageIndex{1}\)б Пристрої з ефектом Холла зазвичай використовуються як датчики, на відміну від пристроїв для збору енергії, оскільки потужність повинна подаватися від цього зовнішнього струму і тому, що кількість виробленої електроенергії, як правило, досить мала.

Силу на зарядах можна знайти з рівняння сили Лоренца. Сила, обумовлена зовнішнім магнітним полем на заряд величини\(q\), задається

\[q\overrightarrow{v} \times \overrightarrow{B} = qv_x\hat{a}_x \times B_z\hat{a}_z = -qB_z\hat{a}_y \nonumber \]

і орієнтується в\(-\hat{a}_y\) напрямку. Позитивні заряди накопичуються на одній стороні напівпровідника, як показано на рис. \(\PageIndex{1}\)c Це накопичення заряду викликає електричне поле, орієнтоване в\(\hat{a}_y\) напрямку, яке виступає проти подальшого накопичення заряду. Заряди накопичуються до досягнення рівноваги, коли сили на заряди в\(\hat{a}_y\) напрямку дорівнюють нулю.

\[\overrightarrow{F} = 0 = Q\left(\overrightarrow{E} + \overrightarrow{v} \times \overrightarrow{B} \right) \nonumber \]

Малюнок\(\PageIndex{1}\): Ілюстрація ефекту Холла.

Напруженість електричного поля може бути виражена як функція напруги,\(V_{AB}\) виміряної по ширині приладу, в\(\hat{a}_y\) напрямку.

\[\overrightarrow{E} = \frac{V_{AB}}{w}\hat{a}_y \nonumber \]

\[q\overrightarrow{E} = -q\overrightarrow{v} \times \overrightarrow{B} \nonumber \]

\[\frac{V_{AB}}{w} = v_xB_z \label{5.1.8} \]

У той час як величина швидкості зарядів\(v_x\) часто не відома, відомий застосований струм\(I_x\), в одиницях ампер. Щільність струму через поперечний переріз приладу є добутком концентрації заряду, сили зарядів і швидкості зарядів.

\[\text{current density} = \frac{I_x}{w \cdot d_{thick}} = q \cdot v_x \cdot p \nonumber \]

З вищенаведеного виразу швидкість може бути виражена термінами струму.

\[v_x = \frac{I_x}{w \cdot d_{thick} \cdot q \cdot p} \label{5.1.10} \]

Рівняння\ ref {5.1.8} і\ ref {5.1.10} можуть бути об'єднані.

\[V_{AB} = \frac{w \cdot I_x \cdot B_z}{w \cdot d_{thick} \cdot q \cdot p} \nonumber \]

Магнітометр - це прилад, який вимірює магнітне поле. Щоб використовувати прилад з ефектом Холла в якості магнітометра, почніть з шматка напівпровідника відомих розмірів і відомої концентрації заряду, а потім подайте струм. Якщо вимірюється напруга, перпендикулярне струму, можна обчислити магнітне поле. Виміряна напруга пропорційно силі зовнішньої щільності магнітного потоку.

\[B_z = \frac{d_{thick} \cdot q \cdot p \cdot V_{AB}}{I_x} \nonumber \]

Напруга легко вимірюється вольтметром, тому ніяких спеціалізованих інструментів не потрібно. Щоб надійно виміряти цю напругу, його часто посилюють.

Крім того, якщо відома напруженість зовнішнього магнітного поля, ефект Холла може бути використаний для вимірювання концентрацій дірок або електронів у шматку напівпровідника. За допомогою деякої алгебри ми можемо записати концентрацію отвору як функцію розмірів напівпровідника, відомої напруженості магнітного поля, прикладеного струму та вимірюваної напруги.

\[p = \frac{I_x \cdot B_z}{d_{thick} \cdot q \cdot V_{AB}} \label{5.1.13} \]

Аналогічний вираз можна знайти, якщо домінуючим носієм заряду є електрони замість дірок. Знак цього вимірюваного напруги також використовується для визначення того, чи є шматок напівпровідника n-типу або p-типу [58].

Опір Холла\(R_H\) - параметр, обернено пропорційний концентрації заряду, і він має одиниці Ом [9] [59]. Для наведених вище припущень опір Холла визначається як

\[R_H = \frac{B_z}{qp} \cdot \frac{w}{l \cdot d_{thick}}. \label{5.1.14} \]

Комбінуючи рівняння\ ref {5.1.13} і\ ref {5.1.14}, його можна записати через виміряну напругу і прикладеного струму.

\[R_H = \frac{V_{AB}}{I_x} \cdot \frac{w}{l} \nonumber \]

Як приклад, припустимо, що в якості пристрою ефекту Холла\(p = 10^{17} cm^{-3}\) використовується шматок кремнію з концентрацією отворів. Пристрій має розміри\(l = 1 cm\), і\(w = 0.2 cm\)\(d_{thick} = 0.2 cm\), і орієнтується воно так, як показано на рис. \(\PageIndex{1}\). Матеріал має питомий опір\(\rho = 0.9 \Omega \cdot cm\). Струм\(I = 1 mA\) подається в\(\hat{a}_x\) напрямку. Прилад знаходиться у зовнішньому магнітному полі\(\overrightarrow{B} = 10^{-5}\hat{a}_z \frac{Wb}{cm^2}\). Якщо вольтметр підключений так, як показано на малюнку, то яку напругу\(V_{AB}\) вимірюють?

\[V_{AB} = \frac{I_x \cdot B_z}{q \cdot d_{thick} \cdot p} = \frac{1^{-3} \cdot 10^{-5}}{1.6 \cdot 10^{-19} \cdot 0.2 \cdot 10^{17}} = 3.1 \cdot 10^{-6} V \nonumber \]

Сигнали в мілівольтовому діапазоні легко виявляються за допомогою стандартного вольтметра, але сигнали в мікровольтовому діапазоні часто можна виміряти з деяким посиленням. Яку вихідну потужність генерує цей пристрій? Ми можемо розрахувати опір по\(\hat{a}_y\) напрямку. Питомий опір кремнію було дано в задачі, а опір\(R\) і питомий опір\(\rho\) пов'язані

\[R = \frac{\rho \cdot \text{length}}{\text{area}}. \nonumber \]

Опір по всій ширині приладу дорівнює

\[R_{width} = \frac{\rho w}{ld_{thick}} = \frac{0.09 \cdot 0.2}{1 \cdot 0.2} = 0.09 \Omega \nonumber \]

Ми можемо використовувати цей розрахунковий опір і виміряну напругу, щоб знайти потужність, перетворену з магнітного поля в електричну потужність пристрою.

\[P = \frac{V^2_{AB}}{R_{width}} = 1.1 \cdot 10^{-11} W \nonumber \]

Ця кількість енергії крихітна. Хоча цей пристрій може зробити корисний датчик, він не зробить корисний пристрій для збору енергії. Він генерує десятки піковат потужності, і для отримання потужності повинен подаватися\(1 mA\) струм.