1.6: Електромагнітні хвилі

Рівняння Максвелла

У цьому тексті$I$ позначають$V$ і постійну напругу і струм відповідно,$v$ а також$i$ позначають змінний струм або змінну напругу і струм. При аналізі схем ми не стурбовані тим, що відбувається поза цими проводами. Нас цікавлять тільки напруга вузлів і струми через дроти. Крім того, напруги та струми в ланцюзі описуються як функції часу,$t$ але не положення$(x, y, z)$. Пристрої, такі як резистори, конденсатори та індуктори теж вважаються точковими і не розширеними щодо положення$(x, y, z)$. Цей набір припущень є лише моделлю. У реальності, якщо два вузли в ланцюзі мають різницю напруг між ними, то обов'язково сила прикладається на сусідні заряди не на шляху проходження ланцюга. Ця сила на одиницю заряду є напруженістю електричного поля$\overrightarrow{E}$. Аналогічно, якщо по проводу протікає струм, обов'язково виникає сила, що чиниться на електрони в сусідніх петель дроту, і ця сила на одиницю струмового елемента є щільністю магнітного потоку$\overrightarrow{B}$. Енергія може зберігатися в електричному або магнітному полі. У наступних розділах ми обговоримо пристрої, включаючи антени, електрооптичні пристрої, фотоелектричні пристрої, лампи та лазери, які перетворюють енергію електромагнітного поля в електрику або з неї. Для опису електромагнітних полів використовуються чотири взаємопов'язані векторні величини. Ці векторні поля є функціями положення$(x, y, z)$ і часу$t$. Чотири векторні поля

• $\overrightarrow{E}(x, y, z, t) =$Напруженість електричного поля в$\frac{V}{m}$
• $\overrightarrow{D}(x, y, z, t) =$Щільність поля зміщення в$\frac{C}{m^2}$
• $\overrightarrow{H}(x, y, z, t) =$Напруженість магнітного поля в$\frac{A}{m}$
• $\overrightarrow{B}(x, y, z, t) =$Щільність магнітного потоку в$\frac{Wb}{m^2}$

У цих виразах$V$ представляє одиниці вольт,$C$ представляє одиниці кулонів,$A$ представляє одиниці ампер і$Wb$ представляє одиниці вебер. Додаткові скорочення для одиниць наведені в Додатку В.

Закон Кулона:

$$\overrightarrow{F} = \frac{Q_1 Q_2 \hat a_r}{4 \pi \epsilon r^{2}} \nonumber$$

говорить нам про те, що заряджені предмети чинять сили на інші заряджені об'єкти. У цьому вираженні$Q_1$ і$Q_2$ знаходяться величини зарядів в кулоні. Величина$\epsilon$ - це діелектрична проникність навколишнього матеріалу в одиницях фарад на метр, і вона обговорюється далі в 1.6.3 і 2.1.3. Величина$r$ - це відстань між зарядами в метрах, і$\hat a_r$ являє собою одиничний вектор, що вказує уздовж напрямку між зарядами. Сила в ньютонах представлена$\overrightarrow{F}$. Протилежні заряди притягують, і подібні заряди відштовхують. Напруженість електричного поля - це сила на одиницю заряду, тому напруженість електричного поля за рахунок точкового заряду задається $$\overrightarrow{E} = \frac{Q \hat a_r}{4 \pi \epsilon r^{2}} \nonumber$$

Ці векторні поля можуть описувати сили на заряди або струми в ланцюзі, а також поза траєкторією ланцюга. Рівняння Максвелла пов'язують мінливі в часі електричні та магнітні поля. Рівняння Максвелла в диференціальній формі:

$$\overrightarrow{\nabla} \times \overrightarrow{E} = -\frac{\partial \overrightarrow{B}}{\partial t} \quad \text{Faraday's Law} \nonumber$$

$$\overrightarrow{\nabla} \times \overrightarrow{H} = \overrightarrow{J} + \frac{\partial \overrightarrow{D}}{\partial t} \quad \text{Ampere's Law} \nonumber$$

$$\overrightarrow{\nabla} \cdot \overrightarrow{D} = \rho_{ch} \quad \text{Gauss's Law for the Electric Field} \nonumber$$

$$\overrightarrow{\nabla} \cdot \overrightarrow{B} = 0 \quad \text{Gauss's Law for the Magnetic Field} \nonumber$$

Додатковими величинами в рівняннях Максвелла є об'ємна щільність струму$\overrightarrow{J}$ в$\frac{A}{m^2}$ і щільність заряду$\rho_{ch}$ в$\frac{C}{m^3}$. У цьому тексті ми не будемо вирішувати рівняння Максвелла, але зіткнемося з посиланнями на них.

Величина$\overrightarrow{\nabla}$ називається оператором del. У декартових координатах він задається

$$\overrightarrow{\nabla} =\hat a_x \frac{\partial}{\partial x} + \hat a_y \frac{\partial}{\partial y} + \hat a_z \frac{\partial}{\partial z}. \nonumber$$

Коли цей оператор діє на скалярну функцію$\overrightarrow{\nabla}f$, він називається градієнтом. Градієнт скалярної функції повертає вектор, що представляє просторову похідну функції, і вказує у напрямку найбільшої зміни цієї функції. У рівняннях Максвелла$\overrightarrow{\nabla}$ діє на векторні, а не скалярні, функції. Операція$\overrightarrow{\nabla} \times \overrightarrow{E}$ називається завивкою, а операція$\overrightarrow{\nabla} \cdot \overrightarrow{E}$ називається розбіжністю. Обидві ці операції являють собою типи просторових похідних векторних функцій. Оператор del підпорядковується ідентичності

$$\nabla^2 =\overrightarrow{\nabla} \cdot \overrightarrow{\nabla}. \nonumber$$

Операція$\nabla^2f$ називається лапласианом скалярної функції, і вона являє собою просторову другу похідну цієї функції.

Електромагнітні хвилі у вільному просторі

Електромагнітні хвилі рухаються крізь порожній простір зі швидкістю світла у вільному просторі$c = 2.998 \cdot 10^8 \frac{m}{s}$, а через інші матеріали зі швидкістю менше$c$. Для синусоїдальної електромагнітної хвилі швидкість поширення є добутком частоти та довжини хвилі $$|\overrightarrow{v}| =f \lambda \nonumber$$

де$|\overrightarrow{v}|$ - величина швидкості в$\frac{m}{s}$,$f$ - частота в Гц, а$\lambda$ довжина хвилі в метрах. У вільному просторі це стає $$c =f \lambda. \nonumber$$

Швидкість світла у вільному просторі пов'язана з двома константами, які описують вільний простір. $$c = \frac{1}{\sqrt{\epsilon_0\mu_0}} \nonumber$$

Діелектрична проникність вільного простору задається тим,$\epsilon_0 = 8.854 \cdot 10^{-12} \frac{F}{m}$ де$F$ представляє фарад, а проникність вільного простору задається тим,$\mu_0 = 1.257 \cdot 10^{-6} \frac{H}{m}$ де$H$ представляє Генріс. (Константи, зазначені в цьому розділі і в Додатку А, округляються до чотирьох значущих цифр.)

У вільному просторі напруженість електричного поля$\overrightarrow{E}$ і щільність потоку зміщення$\overrightarrow{D}$ пов'язані між собою$\epsilon_0$. $$\overrightarrow{D} = \mu_0 \overrightarrow{E} \nonumber$$

Відносно у вільному просторі напруженість магнітного поля$\overrightarrow{H}$ та щільність магнітного потоку$\overrightarrow{B}$ пов'язані між собою$mu_0$. $$\overrightarrow{B} = \mu_0 \overrightarrow{H}. \nonumber$$

Електромагнітні хвилі в матеріалах

Електромагнітні поля дуже по-різному взаємодіють з провідниками і з ізоляторами. Електромагнітні поля не поширюються на досконалі провідники. Замість цього на поверхні накопичуються заряди і струми. Хоча ніякі матеріали не є ідеальними провідниками, часто зустрічаються метали, такі як мідь та алюміній, є дуже хорошими провідниками. Коли ці матеріали поміщаються у зовнішнє електромагнітне поле, поверхневі заряди і струми накопичуються, і електромагнітне поле в матеріалі швидко наближається до нуля. Електромагнітні поля поширюються через ідеальні ізолятори на великі відстані, не розпадаючись, і ніякі заряди або струми не можуть накопичуватися на поверхні, оскільки немає електронів, вільних від їх атомів. У практичних діелектриках електромагнітні хвилі поширюються на великі відстані з дуже невеликим загасанням. Наприклад, оптичні електромагнітні хвилі залишаються досить сильними для виявлення після поширення сотень кілометрів через оптичні волокна, виготовлені з чистого діоксиду кремнію [10, с. 886].

Опір$R$ в Омах, ємність$C$ у фарадах і індуктивність$L$ у Генрі описують електричні властивості пристроїв. Питомий опір$\rho$ в$\Omega m$,$\epsilon$ діелектрична проникність і проникність$\mu$$\frac{H}{m}$ описують електричні властивості матеріалів.$\frac {F}{m}$ Кількість$\rho$$\epsilon$, і$\mu$ описують властивості матеріалів поодинці в той час як кількості$R$$C$, і$L$ включають ефекти матеріалу, форми і розміру пристрою.

Питомий опір$\rho$ - це міра нездатності зарядів або електромагнітних хвиль поширюватися через матеріал. Провідники мають дуже малий питомий опір, тоді як ізолятори мають великий питомий опір. Іноді замість питомого$\sigma =\frac{1}{\rho}$ опору використовується електропровідність$\frac{1}{\Omega m}$, в одиницях. Для пристрою з однорідного матеріалу з довжиною$l$ і площею поперечного перерізу$A$ опір і питомий опір пов'язані $$R =\frac{\rho l}{A}. \nonumber$$

Опір - це міра нездатності зарядів або електромагнітних хвиль протікати через пристрій, тоді як питомий опір є мірою нездатності протікати через матеріал.

Малюнок$\PageIndex{1}$: Геометрія паралельної пластини конденсатора і часткового витку індуктора.

Проникність$\mu$ - це міра здатності матеріалу накопичувати енергію в магнітному полі за рахунок струмів, розподілених по всьому матеріалу. Матеріали також можуть бути описані їх відносною проникністю$\mu_r$, безодичною мірою. $$\mu_r = \frac{\mu}{\mu_0} \nonumber$$

Хоча проникність описує матеріал, індуктивність описує пристрій. Щільність магнітного потоку в матеріалі є масштабованим варіантом напруженості магнітного поля.

$$\overrightarrow{B} =\mu\overrightarrow{H} \nonumber$$

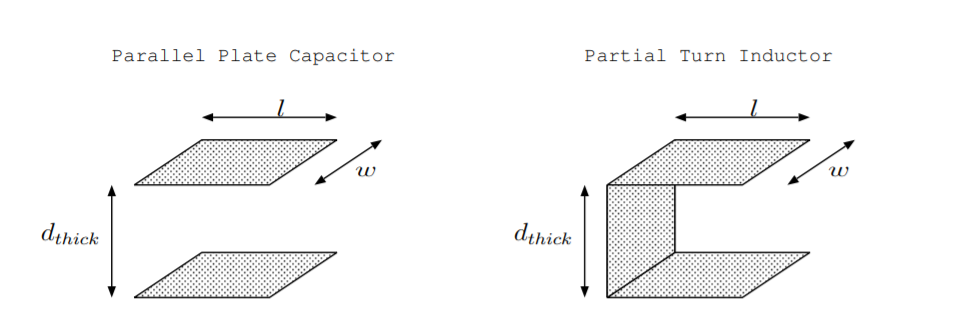
Часто ізолятори мають проникність, близьку до,$mu_0$ тоді як провідники, що використовуються для виготовлення постійних магнітів, мають значно більшу проникність. У правій частині малюнка$\PageIndex{1}$: показана часткова виткова котушка у вакуумі з довжиною$l$$d_{thick}$, товщиною та шириною$w$. Індуктивність і проникність цього пристрою пов'язані [11, с. 311]

$$L =\frac{\mu d_{thick} l}{w}. \nonumber$$

Діелектрична проникність$\epsilon$ - це міра здатності матеріалу зберігати енергію у вигляді електричного поля за рахунок поділу заряду, розподіленого по всьому матеріалу. Матеріали також можуть бути описані їх відносною діелектричною проникністю$\epsilon_r$, безодичною мірою. $$\epsilon_r =\frac{\epsilon}{\epsilon_0} \nonumber$$

Щільність потоку переміщення в матеріалі є масштабованим варіантом напруженості електричного поля. $$\overrightarrow{D} =\epsilon\overrightarrow{E} \nonumber$$

Деякі ізолятори мають діелектричну проникність в сотні разів більше, ніж діелектрична проникність вільного простору. Діелектрична проникність - це міра здатності зберігати енергію в матеріалі, тоді як ємність є мірою здатності зберігати енергію в пристрої.

Рівномірний паралельний пластинчастий конденсатор з площею поперечного перерізу пластин$A =l \cdot w$ і відстанню між пластинами$d_{thick}$$\PageIndex{1}$, показаний на лівій частині малюнка, і він має ємність, $$C =\frac{\epsilon A}{d_{thick}} \nonumber$$ де$\epsilon$ діелектрична проникність ізолятора між пластинами.

Діелектрична проникність, проникність та питомий опір залежать від частоти. У деяких контекстах частотну залежність можна ігнорувати, і протягом більшої частини цього тексту ці величини будуть вважатися константами. В інших контекстах залежність від частоти може бути досить значною. Наприклад, діелектрична проникність напівпровідникових матеріалів є сильною функцією частоти для частот, близьких до напівпровідникового енергетичного розриву. Діелектрична проникність$\epsilon(\omega)$ і питомий опір не$\rho(\omega)$ є незалежними. Якщо одна з них відома як функція частоти і$\mu$ вважається постійною, інша може бути виведена. Цей зв'язок відомий як співвідношення Крамерса Кроніга [10] або іноді як формула діелектричної дисперсії [15].

При обговоренні електричних властивостей пристрою опір, індуктивність та ємність об'єднуються в одну комплексну міру, імпеданс. Так само деякі автори вважають зручним об'єднати питомий опір, діелектричну проникність і проникність в пару комплексних заходів електричних властивостей матеріалів [6]. Визначено складну діелектричну проникність та$\epsilon^* =\epsilon+j\rho$ визначено складну проникність$\mu^* =\mu+j\rho_{mag}$. Величина$\rho$ являє собою питомий опір, який є мірою енергії, перетвореної в тепло, коли заряд протікає через матеріал за рахунок застосованого електричного поля. Величина$\rho_{mag}$ являє собою аналогічну міру енергії, перетвореної в тепло від струмів в прикладеному магнітному полі. Складна діелектрична проникність і проникність в цьому тексті не використовуватимуться.