10.2: Інтерферометрична автокореляція (МАК)
- Page ID
- 32238
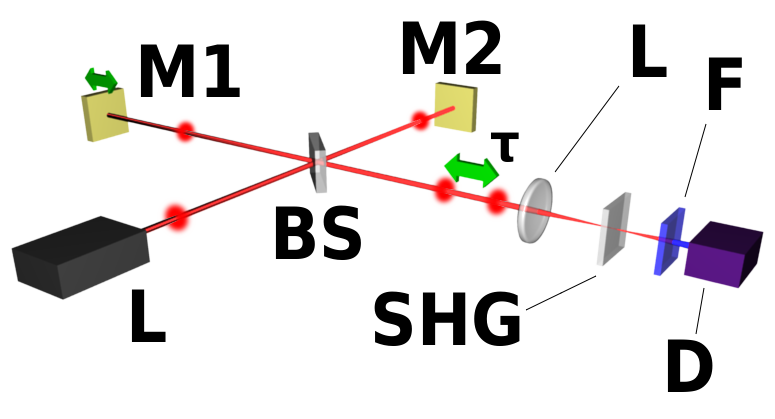
Методом імпульсної характеристики, який також виявляє фазу імпульсу, є інтерферометрична автокореляція, введена Дж. Дільсом [2], (рис. 10.2 а). Вхідний промінь знову розбивається на дві частини і один з них затримується. Однак тепер два імпульси посилаються колінно в нелінійний кристал. Після фільтра виявляється тільки компонент SHG.
Сумарне поле\(E(t,\tau)\) після інтерферометра Майкельсона-інтерферометра задається двома однаковими імпульсами,\(\tau\) затриманими відносно один одного
\[\begin{align*}E(t, \tau) &= E(t + \tau) + E(t) \\[4pt] &= A(t + \tau) e^{j\omega_c (t + \tau)} e^{j \phi_{CE}} + A(t) e^{j \omega_c t} e^{j \phi_{CE}}. \end{align*} \nonumber \]
A (t) - комплексна амплітуда, термін\(e^{i\omega_0 t}\) описує коливання з несучою частотою\(\omega_0\) і\(\phi_{CE}\) є фазою несучої оболонки. Рівняння (10.1.1) пише
\[P^{(2)} (t, \tau) \propto (A(t + \tau) e^{j \omega_c (t + \tau)} e^{j \phi_{CE}} + A(t) e^{j \omega_c t} e^{j\phi_{CE}})^2 \nonumber \]
Це в ідеалі тільки в тому випадку, якщо доріжки для обох балок ідентичні. Якщо, наприклад, використовуються діелектричні або металеві променевіспліттери, в інтерферометрі Майкельсона-інтерферометрі, показаному на малюнку 10.2 (а), що призводять до диференціального зсуву фаз між двома імпульсами. Цього можна уникнути за допомогою точно симетричного етапу затримки, як показано на малюнку 10.1 (b).
Знову ж таки, випромінюване друге гармонічне електричне поле пропорційно поляризації
\[E(t, \tau) \propto (A(t + \tau) e^{j \omega_c (t + \tau)} e^{j \phi_{CE}} + A(t) e^{j \omega_c t} e^{j\phi_{CE}})^2 \nonumber \]
Фотодетектор (або фотомножник) інтегрується над оболонкою кожного окремого імпульсу
\[\begin{array} {rcl} {I(\tau)} & \propto & {\int_{-\infty}^{\infty} |(A(t + \tau) e^{j\omega_c (t + \tau)} + A(t) e^{j\omega_c t})^2|^2 dt.} \\ {} & \propto & {\int_{-\infty}^{\infty} |A^2(t + \tau) e^{j 2 \omega_c (t + \tau)} + 2A(t + \tau) A(t) e^{j\omega_c (t + \tau)} e^{j \omega_c t} + A^2 (t) e^{j 2 \omega_c t}|^2.} \end{array} \nonumber \]
Оцінка абсолютного квадрата призводить до наступного виразу:
\[\begin{array} {rcl} {I(\tau)} & \propto & {\int_{-\infty}^{\infty} [|A(t + \tau)|^4 + 4|A(t + \tau)|^2 |A(t)|^2 + |A(t)|^4} \\ {} & \ & {+2A(t + \tau) |A(t)|^2 A^* (t) e^{j \omega_c \tau} + c.c.} \\ {} & \ & {+2A(t)|A(t + \tau)|^2 A^* (t + \tau) e^{-j \omega_c \tau} + c.c.} \\ {} & \ & {+A^2 (t + \tau) (A^* (t))^2 e^{j2\omega_c \tau} + c.c.]dt.} \end{array} \nonumber \]
Фаза несучої оболонки\(\phi_{CE}\) випадає, оскільки вона ідентична обом імпульсам. Інтерферометрична автокореляційна функція складається з наступних термінів:
\[I(\tau) = I_{back} + I_{int} (\tau) + I_{\omega} (\tau) + I_{2 \omega} (\tau). \label{eq10.2.7} \]
Фоновий сигнал\(I_{back}\):
\[I_{back} = \int_{-\infty}^{\infty} (|A(t + \tau)|^4 + |A(t)|^4) dt = 2 \int_{-\infty}^{\infty} I^2 (t) dt \nonumber \]
Інтенсивність автокореляції\(I_{int} (\tau)\):
\[I_{int} (\tau) = 4\int_{-\infty}^{\infty} |A(t + \tau)|^2 |A(t)|^2 dt = 4 \int_{-\infty}^{\infty} I(t + \tau) \cdot I(t) dt \nonumber \]
Когерентність термін коливається з\(\omega_c\)\(I_{\omega} (\tau)\):
\[I_{\omega} (\tau) = 4 \int_{-\infty}^{\infty} \text{Re} [(I(t) + I(t + \tau)) A^* (t) A(t + \tau) e^{j \omega \tau}] dt \nonumber \]
Когерентність термін коливається з\(2 \omega_c\)\(I_{2\omega} (\tau)\):
\[I_{\omega} (\tau) = 2 \int_{-\infty}^{\infty} \text{Re} [A^2 (t) (A^* (t + \tau))^2 e^{j2\omega \tau}] dt \nonumber \]
Рівняння (\(\ref{eq10.2.7}\)) часто нормалізується відносно інтенсивності фону Iback, що призводить до інтерферометричного автокореляційного сліду
\[I_{IAC} (\tau) = 1 + \dfrac{I_{int}(\tau)}{I_{back}} + \dfrac{I_{\omega}(\tau)}{I_{back}} + \dfrac{I_{2 \omega}(\tau)}{I_{back}}.\label{eq10.2.12} \]
Рівняння (\(\ref{eq10.2.12}\)) є кінцевим рівнянням для нормованої інтерферометричної автокореляції. Термін\(I_{int} (\tau)\) - це автокореляція інтенсивності, виміряна неколінійною генерацією другої гармоніки, як обговорювалося раніше. Отже, усереднена інтерферометрична автокореляція призводить до того, що інтенсивна автокореляція сидить на тлі 1.
На малюнку 10.3 показаний розрахунковий і виміряний ІАК для імпульсу у формі сеха.
Зображення видалено через обмеження авторських прав. Будь ласка, див.: Keller, U., Надшвидка лазерна фізика, Інститут квантової електроніки, Швейцарський федеральний технологічний інститут, ETH Honggerberg—HPT, CH-8093 Цюрих, Швейцарія.
Малюнок 10.3: Обчислені та виміряні інтерферометричні автокореляційні сліди для імпульсу у формі сеха довжиною 10 fs.
Як і у випадку з автокореляцією інтенсивності, при побудові інтерферометрична автокореляція повинна бути також симетричною:
\[I_{IAC} (\tau) = I_{IAC} (-\tau). \nonumber \]
Це вірно лише в тому випадку, якщо шлях променя між двома репліками в установці повністю ідентичний, тобто немає навіть фазового зсуву між двома імпульсами. Зсув фази призведе до зсуву шаблону бахроми, який дуже сильно проявляється в тривалих імпульсах декількох циклів. Щоб уникнути такого розриву симетрії, потрібно розташувати лінію затримки, як показано на малюнку 10.2 b так, щоб кожен імпульс проходив через однакову кількість матеріалу підкладки і зазнавав однакові відбиття.
При\(\tau = 0\), всі інтеграли ідентичні
\[\begin{array} {rcl} {I_{back}} & \equiv & {2 \int |A(t)|^4 dt} \\ {I_{int} (\tau = 0)} & \equiv & {2 \int |A^2(t)|^2 dt = 2 \int |A(t)|^4 dt = I_{back}} \\ {I_{\omega} (\tau = 0)} & \equiv & {2 \int |A(t)|^2 A(t) A^* (t) dt = 2 \int |A(t)|^4 dt = I_{back}}\\ {I_{2\omega} (\tau = 0)} & \equiv & {2\int A^2 (t) A^2 (t)^* dt = 2\int |A(t)|^4 dt = I_{back}} \end{array} \nonumber \]
Потім отримано для інтерферометричної автокореляції при нульовій часовій затримці
\[\begin{array} {l} {I_{IAC} (\tau) |_{\max} = I_{IAC} (0) = 8} \\ {I_{IAC} (\tau \to \pm \infty) = 1} \\ {I_{IAC} (\tau) |_{\min} = 0} \end{array} \nonumber \]
Це важливе співвідношення 1:8 між крилами та вибором МАК, що є хорошим керівництвом для правильного вирівнювання інтерферометричного автокорелятора. Для щебетання пульсу конверт вже не реальний. Щебетання в пульсі призводить до появи вузлів в МАК. На малюнку 10.4 показаний ІАС щебетання сех-імпульсу
\[A(t) = \left ( \text{sech} \left (\dfrac{t}{\tau_p}\right) \right )^{(1 + j\beta)}\nonumber \]
для різних щебетань.
Зображення видалено через обмеження авторських прав.
Будь ласка, дивіться:
Keller, U., Надшвидка лазерна фізика, Інститут квантової електроніки, Швейцарський федеральний технологічний інститут, ETH Ho'nggerberg—HPT, CH-8093 Цюрих, Швейцарія.
Малюнок 10.4: Вплив наростаючого щебетання на МАК.
Інтерферометрична автокореляція нечірпованого імпульсу Сеха
Конверт з нечіркованого січ-імпульсу
\[A(t) = \text{sech} (t/\tau_p) \nonumber \]
Інтерферометрична автокореляція сіх-імпульсу
\[I_{IAC} (\tau) = 1 + \{2 + \cos (2 \omega_c \tau) \} \dfrac{3((\tfrac{\tau}{\tau_p}) \cosh (\tfrac{\tau}{\tau_p}) - \sinh (\tfrac{\tau}{\tau_p}))}{\sinh^3 (\tfrac{\tau}{\tau_p})} + \dfrac{3(\sinh (\tfrac{2\tau}{\tau_p}) - (\tfrac{2\tau}{\tau_p}))}{\sinh^3 (\tfrac{\tau}{\tau_p})} \cos (\omega_c \tau) \nonumber \]
Інтерферометрична автокореляція чірпованого гауссового імпульсу
Комплексна оболонка гауссового імпульсу
\[A(t) = \exp \left [-\dfrac{1}{2} \left (\dfrac{t}{t_p} \right ) (1 + j \beta) \right ]. \nonumber \]
Інтерферометрична автокореляція гауссового імпульсу
\[I_{IAC} (\tau) = 1 + \{2 + e^{-\tfrac{\beta^2}{2} (\tfrac{\tau}{\tau_p})^2} \cos (2 \omega_c \tau) \} e^{-\tfrac{1}{2} (\tfrac{\tau}{\tau_p})^2} + 4e^{-\tfrac{3+\beta^2}{8} (\tfrac{\tau}{\tau_p})^2} \cos \left (\dfrac{\beta}{4} \left (\dfrac{\tau}{\tau_p} \right )^2 \right ) \cos (\omega_c \tau). \nonumber \]
Дисперсія другого порядку
Досить просто обчислити в області Фур'є те, що відбувається при наявності дисперсії.
\[E(t) = A(t) e^{j \omega_c t} \to \tilde{E} (\omega) \nonumber \]
Після поширення через дисперсійне середовище отримаємо в області Фур'є.
\[\tilde{E}' (\omega) = \tilde{E} (\omega) e^{-i\Phi (\omega)}\nonumber \]
і
\[E'(t) = A'9t) e^{j \omega_c t}\nonumber \]
На малюнку 10.5 показана амплітуда імпульсу до і після поширення через середовище з дисперсією другого порядку. Пульс розширюється за рахунок дисперсії. Якщо дисперсія ще більше збільшується, розширення збільшується, і інтерферометричні автокореляційні сліди, показані на малюнку 10.5, розвивають характерний п'єдестал через термін\(I_{int}\). Ширина інтерферометно- рико-чутливої частини залишається колишньою і більше пов'язана з часом когерентності в імпульсі, тобто пропорційно зворотній ширині спектра і не змінюється.
Зображення видалено через обмеження авторських прав.
Будь ласка, дивіться:
Keller, U., Надшвидка лазерна фізика, Інститут квантової електроніки, Швейцарський федеральний технологічний інститут, ETH Ho'nggerberg—HPT, CH-8093 Цюрих, Швейцарія.
Малюнок 10.5: Вплив різних кількостей дисперсії другого порядку на транс-форму, обмежену 10 fs SECH-імпульсу.
Дисперсія третього порядку
Ми очікуємо, що дисперсія третього порядку суттєво впливає на пульс для
\[\dfrac{D_3}{\tau^3} > 1\nonumber \]
який призначений для 10fs секундного імпульсу\(D_3 > (\tfrac{10fs}{1.76})^3 183 fs^3\). На малюнках 10.6 і 10.7 показано вплив на форму імпульсу і інтерферометричну автокореляцію. Термін непарної дисперсії породжує асиметрію в імпульсі. Інтерферометрична автокореляція розвиває характерні вузли в крилах.
Зображення видалено через обмеження авторських прав.
Будь ласка, дивіться:
Keller, U., Надшвидка лазерна фізика, Інститут квантової електроніки, Швейцарський федеральний технологічний інститут, ETH Hongerberg—HPT, CH-8093 Цюрих, Швейцарія.
Малюнок 10.6: Вплив 200 дисперсії\(fs^3\) третього порядку на імпульс 10 fs при центральній довжині хвилі 800 нм і його інтерферометричної автокореляції.
Зображення видалено через обмеження авторських прав.
Будь ласка, дивіться:
Keller, U., Надшвидка лазерна фізика, Інститут квантової електроніки, Швейцарський федеральний технологічний інститут, ETH Ho'nggerberg—HPT, CH-8093 Цюрих, Швейцарія.
Малюнок 10.7: Зміни внаслідок збільшення дисперсії третього порядку від 100-1000\(fs^3\) на імпульсі 10 фс при центральній довжині хвилі 800 нм.
Самофазова модуляція
Самофазова модуляція без компенсації належною негативною дисперсією генерує фазу над імпульсом у часовій області. Ця фаза невидима в автокореляції інтенсивності, однак вона чітко проявляється в МАК, див. Рисунок 10.8 для гауссового імпульсу з піковим нелінійним зсувом фаз\(\phi_0 = \delta A_0^2 = 2\) і рис. 10.8 для нелінійного зсуву фаз\(\phi_0 = 3\).
Зображення видалено через обмеження авторських прав.
Будь ласка, дивіться:
Keller, U., Надшвидка лазерна фізика, Інститут квантової електроніки, Швейцарський федеральний технологічний інститут, ETH Ho'nggerberg—HPT, CH-8093 Цюрих, Швейцарія.
Малюнок 10.8: Зміна форми імпульсу та інтерферометричної автокореляції в імпульсі 10 fs при 800 нм за умови чистої самофазової модуляції, що призводить до нелінійного зсуву фаз\(\phi_0 = 2\).
Зображення видалено через обмеження авторських прав.
Будь ласка, дивіться:
Keller, U., Надшвидка лазерна фізика, Інститут квантової електроніки, Швейцарський федеральний технологічний інститут, ETH Ho'nggerberg—HPT, CH-8093 Цюрих, Швейцарія.
Малюнок 10.9: Зміна форми імпульсу та інтерферометричної автокореляції в імпульсі 10 fs при 800 нм за умови чистої самофазової модуляції, що призводить до нелінійного зсуву фаз\(\phi_0 = 3\).
З досвіду, отриманого, розглядаючи вищезазначені IAC-сліди для імпульсів, що проходять дисперсії другого та третього порядку, а також самофазової модуляції, ми робимо висновок, що загалом неможливо передбачити чисто, дивлячись на IAC, які фазові збурень може мати імпульс. Тому завжди було бажання однозначно реконструювати електричне поле щодо амплітуди та фази з виміряних даних. Насправді можна чітко показати, що амплітуда і фаза імпульсу можуть бути виведені однозначно від МАК і виміряного спектра до амбігітуїну часового розвороту [1]. Крім того, показано, що для реконструкції імпульсу достатньо перехресної кореляції імпульсу з реплікою, щебенетою у відомому середовищі та спектром імпульсу [3]. Так як спектр імпульсу вже заданий тільки фаза повинна бути визначена. Якщо передбачається певна фаза, можна обчислити електричне поле і виміряну крос-кореляцію або IAC. Мінімізація похибки між виміряною крос-кореляцією або IAC дасть дедротову спектральну фазу. Ця процедура отримала назву PICASO (фаза та інтенсивність від перехресної кореляції та лише спектру).
Зверніть увагу, також замість вимірювання автокореляції та інтерферометричної автокореляції з SHG можна також використовувати двофотонне поглинання або поглинання більш високого порядку в напівпровідниковому матеріалі (Лазер або світлодіод) [4].
Однак сьогодні двома широко використовуваними методами імпульсної характеристики є частотно-вирішена оптична решітка (FROG) та спектральна фазова інтерфером-запис для прямої реконструкції електричного поля (SPIDER)
