4.1: Рівняння швидкості
- Page ID
- 32177
У розділі 2.5 ми вивели для взаємодії дворівневого атома з лазерним полем, що поширює праворуч рівняння руху (2.5.13) і (2.5.14), які наведені тут знову:
\[\left ( \dfrac{\partial}{\partial z} + \dfrac{1}{v_g} \dfrac{\partial}{\partial t} \right ) A(z, t) = \dfrac{N\hbar}{4T_2 E_s} w (z, t) A(z, t), \label{4.1.1} \]
\[\dot{w} = -\dfrac{w - w_0}{T_1} + \dfrac{|A(z,t)|^2}{E_s} w(z, t), \label{4.1.2} \]
де швидкість релаксації енергії,\(T_1\)\(v_g\) групова швидкість у матеріалі господаря, де вбудовані два атоми рівня\(E_s = I_sT_1\), флюенс насичення [\(J/cm^2\)], середовища. І\(I_s\) інтенсивність насичення відповідно до рівняння (2.4.7)
\[I_s = \left [\dfrac{2T_1T_2Z_F}{\hbar} \dfrac{|\vec{M} \hat{\vec{E}}|^2}{|\hat{\vec{E}}|^2} \right ]^{-1},\nonumber \]
яка пов'язує інтенсивність насичення з мікроскопічними параметрами переходу, такими як поздовжня і поперечна швидкості релаксації, а також дипольний момент переходу.
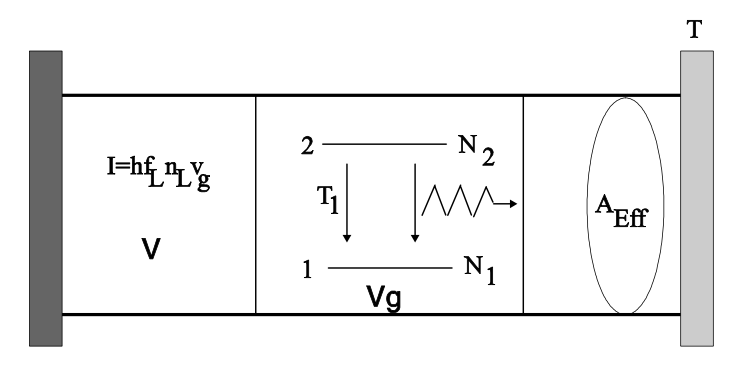
У багатьох випадках зручніше нормалізувати рівняння\ ref {4.1.1} і\ ref {4.1.2} до популяцій на рівні\(\text{e}\)\(\text{g}\) і/або 2\(N_2\) і 1 відповідно і\(N_1\), і щільності фотонів\(n_L\), в режимі взаємодії з атомами і рухаються на відповідному групова швидкість, vg, див. Рис. 4.1. Інтенсивність\(I\) в режимі, що поширюється з\(v_g\) груповою швидкістю з режимним об'ємом,\(V\) пов'язана з кількістю фотонів,\(N_L\) що зберігаються в режимі з\(V\) об'ємом на
\[I = hf_L \dfrac{N_L}{2^*V} v_g = \dfrac{1}{2^*} hf_Ln_Lv_g, \nonumber \]
де\(hf_L\) - енергія фотонів. \(2^* = 2\)для лінійного лазерного резонатора (тоді тільки половина фотонів йде в одному напрямку), і\(2^* = 1\) для кільцевого лазера. У цій першій обробці розглядається випадок незалежних від простору рівнянь швидкості, тобто ми припускаємо, що лазер коливається в одному режимі, а густини енергії накачування і режиму рівномірні всередині лазерного матеріалу. З взаємодією поперечний переріз\(\sigma\) визначається як
\[\sigma = \dfrac{hf_L}{2^*I_s T_1},\label{eq4.1.4} \]
і множення рівняння (??) з кількістю атомів в режимі отримуємо
\[\dfrac{d}{dt} (N_2 - N_1) = -\dfrac{(N_2 - N_1)}{T_1} - \sigma (N_2 - N_1) v_g n_L + R_p \nonumber \]
Зверніть увагу,\(v_gn_L\) це потік фотонів, таким чином σ - це поперечний переріз стимульованого випромінювання між атомами і фотонами. \(R_p\)це швидкість накачування в верхній лазерний рівень. Аналогічне рівняння швидкості можна вивести для густини фотонів
\[\dfrac{d}{dt} n_L = -\dfrac{n_L}{\tau_p} + \dfrac{l_g}{L} \dfrac{\sigma v_g}{V_g} [N_2 (n_L + 1) - N_1 n_L].\label{eq4.1.6} \]
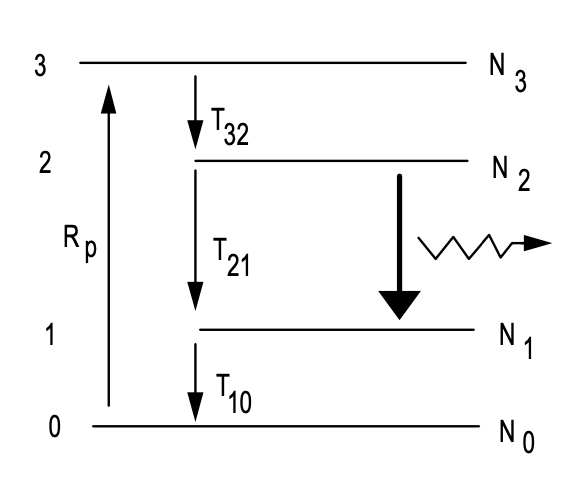
Ось час життя фотонів у порожнині або порожнині час розпаду і той, що в еквалайзері.\(\tau_p\) (\(\ref{4.1.6}\)) припадає на спонтанне випромінювання, що еквівалентно стимульованому випромінюванню одним фотоном, що займає режим. \(V_g\)- це обсяг активного середовища посилення. Для лазерної порожнини з напівпрозорим дзеркалом з передачею\(T\), що виробляє невеликі втрати потужності\(2l = - \ln(1 - T) \approx T\) (для малих\(T\)) на кругообіг в порожнині, час розпаду порожнини становить\(\tau_p = 2l/T_R\), якщо\(T_R = 2^*L/c_0\) це час кругообігу в лінійній порожнині з оптичною довжиною\(2L\) або кільцем порожнину з оптичною довжиною\(L\). Оптична довжина\(L\) - це сума оптичної довжини в середовищі посилення\(n_{group} l_g\) та довжини порожнини вільного простору\(l_a\). Внутрішні втрати можна лікувати аналогічним чином і сприяти часу розпаду порожнини. Зверніть увагу, швидкість розпаду при інверсії при відсутності поля\(1/T_1\), обумовлена не тільки спонтанним випромінюванням, але і є результатом нерадіаційних процесів розпаду. Дивіться, наприклад, систему чотирьох рівнів, показану на малюнку 4.2. У межі, де популяції третього і першого рівня дорівнюють нулю, через швидкі темпи релаксації\(T_{32}\)\(T_{10} \to 0\), т. Е.
\[\dfrac{d}{dt} N_2 = -\dfrac{N_2}{\tau_L} - \sigma v_g N_2 n_L + R_p \nonumber \]
\[\dfrac{d}{dt} n_L = -\dfrac{n_L}{\tau_p} + \dfrac{l_g}{L} \dfrac{\sigma v_g}{V_g} N_2 (n_L + 1). \nonumber \]
де\(\tau_L = T_{21}\) - термін служби верхнього лазерного рівня. Експериментально число фотонів та інверсія в лазерному резонаторі є не дуже зручними величинами, тому ми нормалізуємо обидва рівняння до посилення амплітуди в зворотному напрямку, що\(g = \dfrac{l_g}{L} \dfrac{\sigma v_g}{2V_g} N_2 T_R\) відчувається світлом та циркулюючою внутрішньорезонаторною потужністю\(P = I \cdot A_{eff}\)
\[\dfrac{d}{dt} g = -\dfrac{g-g_0}{\tau_L} - \dfrac{gP}{E_{sat}} \nonumber \]
\[\dfrac{d}{dt} P = -\dfrac{1}{\tau_p} P + \dfrac{2g}{T_R} (P + P_{vac}), \nonumber \]
із
\[E_s = I_s A_{eff} \tau_{L} = \dfrac{hf_L}{2^* \sigma} \nonumber \]
\[P_{sat} = E_{sat}/\tau_L \nonumber \]
\[P_{vac} = hf_L v_g/2^* L = hf_L/T_R \nonumber \]
\[g_0 = \dfrac{2^* v_g R_p}{2A_{eff} c_0} \sigma \tau_L,\label{eq4.1.14} \]
невеликий сигнал зворотного посилення лазера. Зверніть увагу, коефіцієнт двох перед виграшем і втратою обумовлений тим, що\(g\) і\(l\) є посилення і втрати щодо амплітуди. Рівняння\ ref {eq4.1.14} з'ясовує, що цифра заслуги, яка характеризує малий посилення сигналу, досяжний з певним лазерним матеріалом, є\(\sigma \tau_L\) -продуктом.
| Лазерне середовище | Довжина хвилі\(\lambda_0\) (\(n\)м) | Поперечний\(\sigma\) переріз (\(\text{cm}^2\)) | Верхня Св. Термін служби\(\tau_L\) (\(\mu\)и) | Ширина лінії\(\Delta f_{FWHM} = \tfrac{2}{T_2} (\text{THz})\) | Тип | Реф. індекс\(n\) |
|---|---|---|---|---|---|---|
| \(\text{Nd}^{3+}: \ce{YAG}\) | \ (\ лямбда_0\) (\(n\)m) ">1,064 | \ (\ сигма\) (\(\text{cm}^2\)) ">\(4.1 \cdot 10^{-19}\) | \ (\ tau_l\) (\(\mu\)s) ">1,200 | \ (\ Дельта f_ {FWHM} =\ tfrac {2} {T_2} (\ текст {ТГц})\) ">0.210 | Ч | \ (n\) ">1,82 |
| \(\text{Nd}^{3+}: \ce{LSB}\) | \ (\ лямбда_0\) (\(n\)m) ">1,062 | \ (\ сигма\) (\(\text{cm}^2\)) ">\(1.3 \cdot 10^{-19}\) | \ (\ tau_l\) (\(\mu\)s) ">87 | \ (\ Дельта f_ {FWHM} =\ tfrac {2} {T_2} (\ текст {ТГц})\) ">1.2 | Ч | \ (n\) ">1.47 (ne) |
| \(\text{Nd}^{3+}: \ce{YLF}\) | \ (\ лямбда_0\) (\(n\)m) ">1,047 | \ (\ сигма\) (\(\text{cm}^2\)) ">\(1.8 \cdot 10^{-19}\) | \ (\ тау_л\) (\(\mu\)и) ">450 | \ (\ Дельта f_ {FWHM} =\ tfrac {2} {T_2} (\ текст {ТГц})\) ">0.390 | Ч | \ (n\) ">1.82 (ne) |
| \(\text{Nd}^{3+}: \ce{YVO4}\) | \ (\ лямбда_0\) (\(n\)m) ">1,064 | \ (\ сигма\) (\(\text{cm}^2\)) ">\(2.5 \cdot 10^{-19}\) | \ (\ tau_l\) (\(\mu\)s) ">50 | \ (\ Дельта f_ {FWHM} =\ tfrac {2} {T_2} (\ текст {ТГц})\) ">0.300 | Ч | \ (n\) ">2.19 (ne) |
| \(\text{Nd}^{3+}: \ce{glass}\) | \ (\ лямбда_0\) (\(n\)m) ">1,054 | \ (\ сигма\) (\(\text{cm}^2\)) ">\(4 \cdot 10^{-20}\) | \ (\ тау_л\) (\(\mu\)и) ">350 | \ (\ Дельта f_ {FWHM} =\ tfrac {2} {T_2} (\ текст {ТГц})\) ">3 | Ч/Я | \ (n\) ">1.5 |
| \(\text{Er}^{3+}: \ce{glass}\) | \ (\ лямбда_0\) (\(n\)m) ">1,55 | \ (\ сигма\) (\(\text{cm}^2\)) ">\(6 \cdot 10^{-21}\) | \ (\ tau_l\) (\(\mu\)s) ">10,000 | \ (\ Дельта f_ {FWHM} =\ tfrac {2} {T_2} (\ текст {ТГц})\) ">4 | Ч/Я | \ (n\) ">1,46 |
| Рубін | \ (\ лямбда_0\) (\(n\)m) ">694.3 | \ (\ сигма\) (\(\text{cm}^2\)) ">\(2 \cdot 10^{-20}\) | \ (\ tau_l\) (\(\mu\)s) ">1,000 | \ (\ Дельта f_ {FWHM} =\ tfrac {2} {T_2} (\ текст {ТГц})\) ">0.06 | Ч | \ (n\) ">1,76 |
| \(\text{Ti}^{3+}: \ce{Al2O3}\) | \ (\ лямбда_0\) (\(n\)m) ">660-1180 | \ (\ сигма\) (\(\text{cm}^2\)) ">\(3 \cdot 10^{-19}\) | \ (\ tau_l\) (\(\mu\)s) ">3 | \ (\ Дельта f_ {FWHM} =\ tfrac {2} {T_2} (\ текст {ТГц})\) ">100 | Ч | \ (n\) ">1,76 |
| \(\text{Cr}^{3+}: \ce{LiSAF}\) | \ (\ лямбда_0\) (\(n\)m) ">760-960 | \ (\ сигма\) (\(\text{cm}^2\)) ">\(4.8 \cdot 10^{-20}\) | \ (\ tau_l\) (\(\mu\)s) ">67 | \ (\ Дельта f_ {FWHM} =\ tfrac {2} {T_2} (\ текст {ТГц})\) ">80 | Ч | \ (n\) ">1.4 |
| \(\text{Cr}^{3+}: \ce{LiCAF}\) | \ (\ лямбда_0\) (\(n\)м) ">710-840 | \ (\ сигма\) (\(\text{cm}^2\)) ">\(1.3 \cdot 10^{-20}\) | \ (\ tau_l\) (\(\mu\)и) ">170 | \ (\ Дельта f_ {FWHM} =\ tfrac {2} {T_2} (\ текст {ТГц})\) ">65 | Ч | \ (n\) ">1.4 |
| \(\text{Cr}^{3+}: \ce{LiSGAF}\) | \ (\ лямбда_0\) (\(n\)м) ">740-930 | \ (\ сигма\) (\(\text{cm}^2\)) ">\(3.3 \cdot 10^{-20}\) | \ (\ tau_l\) (\(\mu\)s) ">88 | \ (\ Дельта f_ {FWHM} =\ tfrac {2} {T_2} (\ текст {ТГц})\) ">80 | Ч | \ (n\) ">14 |
| Хе-Не | \ (\ лямбда_0\) (\(n\)m) ">632.8 | \ (\ сигма\) (\(\text{cm}^2\)) ">\(1 \cdot 10^{-13}\) | \ (\ tau_l\) (\(\mu\)s) ">0.7 | \ (\ Дельта f_ {FWHM} =\ tfrac {2} {T_2} (\ текст {ТГц})\) ">0.0015 | Я | \ (n\) ">~1 |
| \(\ce{Ar+}\) | \ (\ лямбда_0\) (\(n\)m) ">515 | \ (\ сигма\) (\(\text{cm}^2\)) ">\(3 \cdot 10^{-12}\) | \ (\ tau_l\) (\(\mu\)s) ">0.07 | \ (\ Дельта f_ {FWHM} =\ tfrac {2} {T_2} (\ текст {ТГц})\) ">0.0035 | Я | \ (n\) ">~1 |
| \(\ce{CO2}\) | \ (\ лямбда_0\) (\(n\)м) ">10,600 | \ (\ сигма\) (\(\text{cm}^2\)) ">\(3 \cdot 10^{-18}\) | \ (\ tau_l\) (\(\mu\)s) ">2 900 000 | \ (\ Дельта f_ {FWHM} =\ tfrac {2} {T_2} (\ текст {ТГц})\) ">0.000060 | Ч | \ (n\) ">~1 |
| Родамін-6Г | \ (\ лямбда_0\) (\(n\)m) ">560-640 | \ (\ сигма\) (\(\text{cm}^2\)) ">\(3 \cdot 10^{-16}\) | \ (\ tau_l\) (\(\mu\)s) ">0.0033 | \ (\ Дельта f_ {FWHM} =\ tfrac {2} {T_2} (\ текст {ТГц})\) ">5 | Ч | \ (n\) ">1,33 |
| напівпровідників | \ (\ лямбда_0\) (\(n\)м) ">450-30,000 | \ (\ сигма\) (\(\text{cm}^2\)) ">~\(10^{-14}\) | \ (\ tau_l\) (\(\mu\)s) ">~ 0,002 | \ (\ Дельта f_ {FWHM} =\ tfrac {2} {T_2} (\ текст {ТГц})\) ">25 | Ч/Я | \ (n\) ">3-4 |
Чим більше цей продукт, тим більшим є малий коефіцієнт посилення сигналу (\(g_0\)) досяжний з певним лазерним матеріалом. Таблиця 4.1
Від ур. (2.4.7) і (\(\ref{eq4.1.4}\)) ми знаходимо наступний зв'язок між перетином взаємодії переходу та його мікроскопічними параметрами, такими як ширина лінії, дипольний момент та швидкість релаксації енергії
\[\sigma = \dfrac{hf_L}{I_{sat} T_1} = \dfrac{2T_2}{\hbar^2 Z_F} \dfrac{|\vec{M} \hat{\vec{E}}|^2}{|\hat{\tilde{E}}|^2}.\nonumber \]
Це рівняння говорить нам, що широкосмугові лазерні матеріали, природно, показують менші перерізи посилення, якщо дипольний момент однаковий.
