4.4: Q-перемикання
- Page ID
- 32167
Зображення видалено через обмеження авторських прав. Будь ласка, дивіться: Keller, U., Надшвидка лазерна фізика, Інститут квантової електроніки, Швейцарський федеральний технологічний інститут, ETH Ho'nggerberg—HPT, CH-8093 Цюрих, Швейцарія.
Малюнок 4.5: Динаміка посилення і втрат активно Q-перемикається лазера.
Енергія, що зберігається в лазерному середовищі, може бути вивільнена раптово, збільшивши Q-значення порожнини, щоб лазер досяг порогу. Це можна зробити активно, наприклад, швидко перемістивши одне з дзеркал резонатора на місце або пасивно, помістивши насичуваний поглинач в резонатор [1, 16]. Хеллварт вперше запропонував цей метод лише через рік після винаходу лазера. Як груба орієнтація для твердотільного лазера, наступне співвідношення для відповідних часових шкал, як правило, є дійсним
\[\tau_L \gg T_R \gg \tau_p. \nonumber \]
Активне Q-перемикання
На малюнку 4.5 показана принципова динаміка активної добротності лазера. Лазер накачується імпульсом насоса з довжиною на порядок життя верхнього стану, в той час як внутрішньопорожнині втрати тримаються досить високими, так що лазер не може досягти порогу. Тому лазерне середовище виступає в ролі накопичувача енергії. Енергія розслабляється лише спонтенними і невипромінювальними переходами. Тоді раптом внутрішньопорожнинна втрата зменшується, наприклад, дзеркалом, що обертається порожниною. Лазер накачується вище порогу, і світлове поле нарощується експоненціально з чистим коефіцієнтом посилення, поки енергія імпульсу не наблизиться до енергії насичення середовища посилення. Посилення насичується і витягується, так що лазер відключається самим імпульсом.
Типовий активно Q-імпульс асиметричний: час підйому пропорційно до чистого посилення після того, як Q-значення порожнини активно перемикається на високе значення. Інтенсивність світла наростає пропорційна\(2g_0/T_R\). Коли посилення виснажується, час падіння здебільшого залежить від часу розпаду порожнини αp. Для коротких імпульсів з модуляцією добротності необхідна коротка довжина порожнини, високий коефіцієнт посилення і велика зміна порожнини Q. Якщо Q-перемикач не швидкий, ширина імпульсу може бути обмежена швидкістю перемикача. Типові електрооптичні і акустооптичні вимикачі - 10 нс і 50 нс відповідно
Зображення видалено через обмеження авторських прав. Будь ласка, дивіться: Keller, U., Надшвидка лазерна фізика, Інститут квантової електроніки, Швейцарський федеральний технологічний інститут, ETH Ho'nggerberg—HPT, CH-8093 Цюрих, Швейцарія.
Малюнок 4.6: Асиметричний активно Q-імпульс.
Наприклад, з\(\ce{Nd:YAG}\) мікрочіповим лазером з діодною накачуванням [6] за допомогою електрооптичного перемикача на основі імпульсів з\(\ce{LiTaO3}\) модуляцією добротності коротше 270 пс при частоті повторення 5 кГц були сформовані пікові потужності 25 кВт при середній потужності 34 мВт, а енергія імпульсів 6,8\(\mu\) Дж (рис. 4.7).
Зображення видалено через обмеження авторських прав. Будь ласка, дивіться: Кафка, Дж., і Т. «Волоконний лазер, легований ербієм, з формуванням солітонних імпульсів». Оптика Листи 14 (1989): 1269-1271.
Малюнок 4.7: Мікрочіп-лазер з модуляцією добротності за допомогою електрооптичного перемикача. Імпульс вимірюється за допомогою діапазону відбору проб [8]
Аналогічні результати були досягнуті з Nd:YLF [7] і відповідна установка показана на малюнку 4.8.
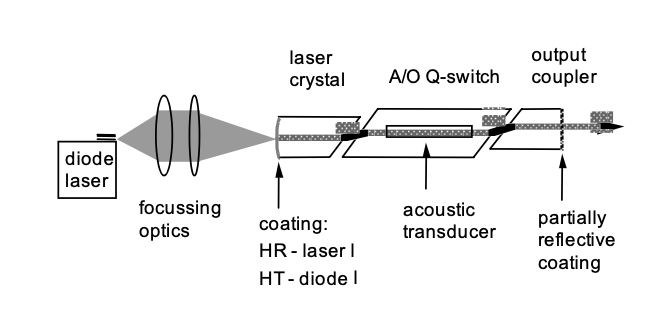
Одночастотні імпульси з Q-комутацією
Лазери з модуляцією добротності забезпечують стабільний вихід лише в тому випадку, якщо вони коливаються однієї частоти. Зазвичай це не досягається автоматично. Одним із способів досягнення цього є посів одночастотним лазером під час роботи з модуляцією добротності, так що вже існує популяція в одному з поздовжніх режимів перед нарощуванням імпульсу. Цей режим витягне всю енергію раніше, ніж інші режими зможуть це зробити, див. Рисунок 4.9
Зображення видалено через обмеження авторських прав. Будь ласка, дивіться: Keller, U., Надшвидка лазерна фізика, Інститут квантової електроніки, Швейцарський федеральний технологічний інститут, ETH Ho'nggerberg—HPT, CH-8093 Цюрих, Швейцарія.
Малюнок 4.9: Вихідна інтенсивність лазера з модуляцією добротності без а) і з посівом б).
Інша можливість досягнення одномодового виходу - це або використання еталона в порожнині, або зробити порожнину настільки короткою, що тільки один поздовжній режим знаходиться в межах смуги посилення (рис. 4.10). Зазвичай це відбувається лише в тому випадку, якщо довжина порожнини знаходиться на порядку перегляду міліметрів або нижче.Мікрочіповий лазер [6] [11] [10] може поєднуватися з електрооптичним модулятором для досягнення дуже компактних лазерів високої пікової потужності з субнаносекундною шириною імпульсу (рис. 4.7).
Зображення видалено через обмеження авторських прав. Будь ласка, дивіться: Keller, U., Надшвидка лазерна фізика, Інститут квантової електроніки, Швейцарський федеральний технологічний інститут, ETH Ho'nggerberg—HPT, CH-8093 Цюрих, Швейцарія.
Малюнок 4.10: У мікрочіповому лазері резонатор може бути настільки коротким, що в межах смуги посилення є тільки один поздовжній режим.
Теорія активного Q-перемикання
Ми хочемо отримати деяке уявлення про нарощування імпульсів і занепад активно Q-перемикається імпульсу. Розглянемо ідеальну ситуацію, коли втрати порожнини лазера можуть миттєво перемикатися з високого значення на низьке, тобто коефіцієнт якості переключається з низького значення відповідно на високе (рис.: 4.11)
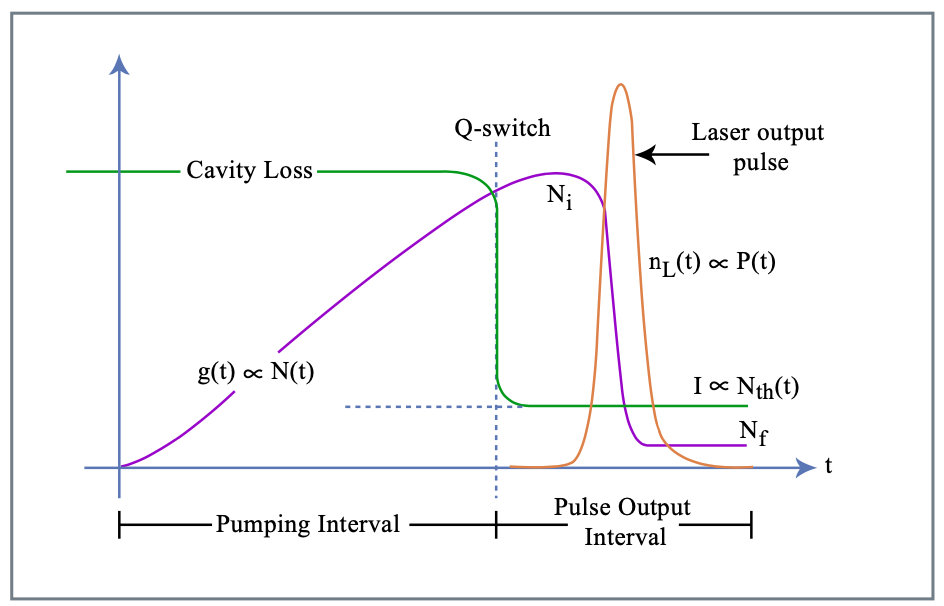
Інтервал відкачування
Під час прокачування з постійною швидкістю накачування\(R_p\), пропорційною малому посиленню сигналу\(\text{g}_0\), нарощується інверсія. Оскільки поля немає, коефіцієнт посилення відповідає простому рівнянню:
\[\dfrac{d}{dt} \text{g} = -\dfrac{\text{g} - \text{g}_0}{\tau_L}, \nonumber \]
або
\[\text{g}(t) = \text{g}_0 (1 - e^{-t/\tau_L}), \nonumber \]
Імпульсна фаза нарощування:
Припускаючи миттєве перемикання втрат порожнини, ми шукаємо приблизне рішення рівнянь швидкості, починаючи з початкового посилення або інверсії\(\text{g}_i = hf_LN_{2i}/(2E_{sat}) = hf_LN_i/(2E_{sat})\), ми можемо зберегти індекс подалі, оскільки існує лише верхня державна популяція. Далі припускаємо, що під час нарощування імпульсу стимульована швидкість випромінювання є домінуючим терміном, що змінює інверсію. Тоді рівняння швидкості спрощують\(\tau\)
\[\dfrac{d}{dt} \text{g} = -\dfrac{\text{g}P}{E_{sat_p}} \nonumber \]
\[\dfrac{d}{dt} P = \dfrac{2(\text{g} - l)}{T_R} P, \nonumber \]
в результаті чого
\[\dfrac{dP}{d\text{g}} = \dfrac{2E_{sat}}{T_R} \left (\dfrac{l}{\text{g}} - 1\right ).\label{eq4.4.6} \]
Ми використовуємо наступні початкові умови для внутрішньопорожнинної потужності\(P (t = 0) = 0\) та початкового посилення\(\text{g}(t = 0) = \text{g}_i = r \cdot l\). Зверніть увагу,\(r\) означає, скільки разів лазер накачується вище порогового значення після того, як Q-перемикач працює і внутрішньопорожнині втрати були зменшені до\(l\). Тоді\(\ref{eq4.4.6}\) можна безпосередньо вирішити, і ми отримаємо
\[P(t) = \dfrac{2 E_{sat}}{T_R} \left (\text{g}_i - \text{g} (t) + l \ln \dfrac{\text{g} (t)}{\text{g}_i} \right ). \nonumber \]
З цього рівняння можна вивести максимальну потужність імпульсу, так як зростання внутрішньопорожнинної потужності припиниться при зниженні посилення до втрат\(g(t) = l\), (рис. 4.11)
\[P_{\max} = \dfrac{2lE_{sat}}{T_R} (r - 1 - \ln r) \nonumber \]
\[= \dfrac{E_{sat}}{\tau_p} (r - 1 - \ln r).\label{eq4.4.9} \]
Це перша важлива величина генерується імпульсу і показана нормалізованою на малюнку 4.12.
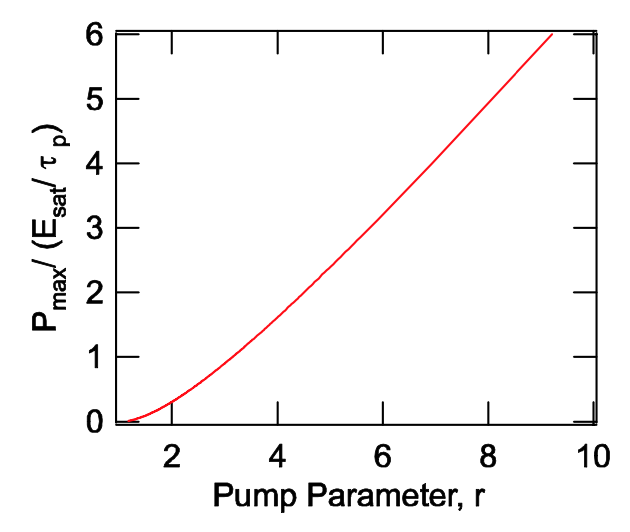
Далі ми можемо знайти остаточне посилення\(\text{g}_f\), яке досягається після завершення імпульсного випромінювання, тобто коли права сторона (4.38) зникає
\[\left (\text{g}_i - \text{g}_f + l \ln \left ( \dfrac{\text{g}_f}{\text{g}_i} \right ) \right ) = 0 \nonumber \]
Використовуючи параметр pump\(r = \text{g}_i/l\), це дає як вираз співвідношення між кінцевим і початковим коефіцієнтом посилення або між остаточною та початковою інверсією
\[1 - \dfrac{\text{g}_f}{\text{g}_i} + \dfrac{1}{r} \ln \left (\dfrac{\text{g}_f}{\text{g}_i} \right ) = 0, \nonumber \]
\[1 - \dfrac{N_f}{N_i} + \dfrac{1}{r} \ln \left ( \dfrac{N_f}{N_i} \right ) = 0,\label{eq4.4.12} \]
який залежить тільки від параметра насоса. Якщо припустити далі, що внутрішніх втрат немає, то можна оцінити енергію імпульсу, що генерується
\[E_P = (N_i - N_f) h f_L. \nonumber \]
Це також дорівнює енергії імпульсу, пов'язаної з виходом, оскільки внутрішні втрати не передбачаються. Таким чином, якщо остаточна інверсія стає малою, вся енергія, що зберігається в середовищі посилення, може бути витягнута. Визначаємо ефективність видобутку енергії\(\eta\)
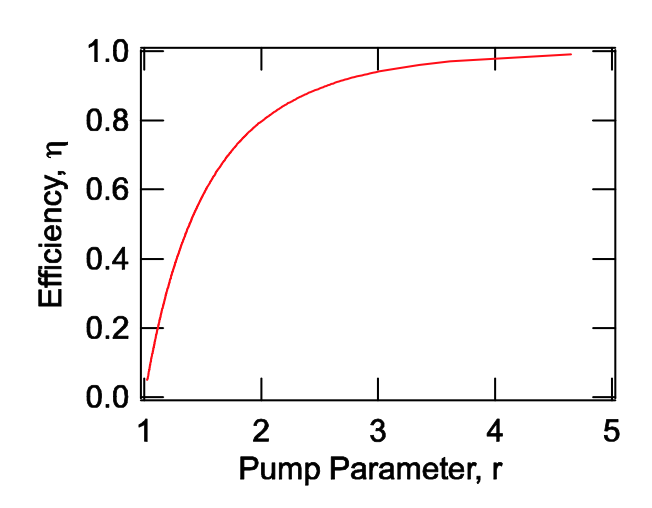
\[\eta = \dfrac{N_i - N_f}{N_i}, \nonumber \]
що говорить нам, скільки спочатку накопиченої енергії можна витягти за допомогою еквалайзера. (\(\ref{eq4.4.12}\))
\[\eta + \dfrac{1}{r} \ln (1 - \eta) = 0. \nonumber \]
Ця ефективність побудована на малюнку 4.13.
Зверніть увагу, ефективність видобутку енергії залежить тільки від параметра насоса\(r\). Тепер випромінювану енергію імпульсу можна записати як
\[E_P = \eta (r) N_i h f_L.\label{eq4.4.16} \]
і ми можемо оцінити ширину імпульсу випромінюваного імпульсу по співвідношенню між енергією імпульсу і піковою потужністю за допомогою (\(\ref{eq4.4.9}\)) і (\(\ref{eq4.4.16}\))
\[\begin{array} {rcl} {\tau_{Pulse}} & = & {\dfrac{E_P}{2lP_{peak}} = \tau_p \dfrac{\eta (r)}{(r - 1 - \ln r)} \dfrac{N_i hf_L}{2lE_{sat}}} \\ {} & = & {\tau_p \dfrac{\eta (r)}{(r - 1 - \ln r)} \dfrac{\text{g}_i}{l}} \\ {} & \ & {\tau_p \dfrac{\eta (r) \cdot r}{(r - 1 - \ln r)}.} \end{array} \nonumber \]
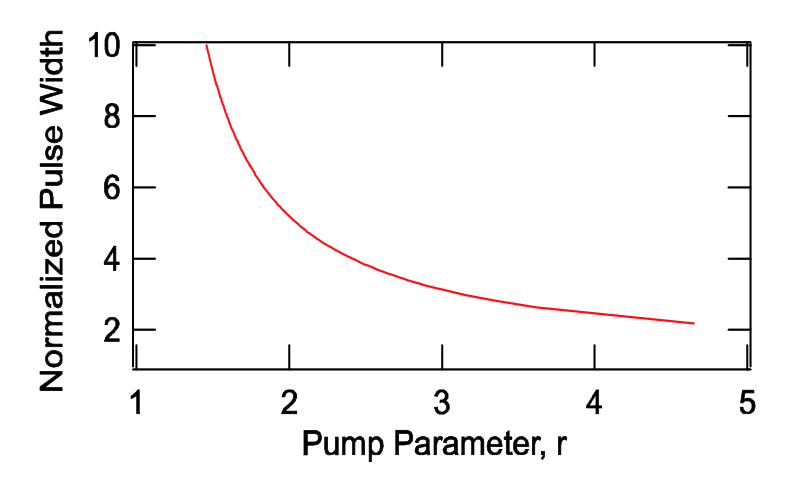
Нормована до часу розпаду порожнини ширина імпульсу\(\tau_p\) показана на малюнку 4.14.
Пасивне Q-перемикання
У разі пасивного Q-перемикання внутрішньопорожнинна модуляція втрат попередньо формується насиченим поглиначем, що вносить великі втрати при низькій інтенсивності світла і малі втрати для високої інтенсивності.
Релаксаційні коливання відбуваються за рахунок періодичного обміну енергією, що зберігається в лазерному середовищі інверсією і світловим полем. Без насичуваного абсорбера ці коливання гасять. Якщо з якихось причин в системі є два великих посилення, світлове поле може швидко нарощуватися. Особливо для низького коефіцієнта посилення поперечного перерізу зворотної дії зростаючого лазерного поля на інверсії слабке, і воно може рости далі. Цьому зростанню сприяє наявність втрат, які насичують інтенсивністю світла. Лазер стає нестабільним, зростання інтенсивності поля до тих пір, поки посилення не насичується нижче чистих втрат, див. Рис.4.15.
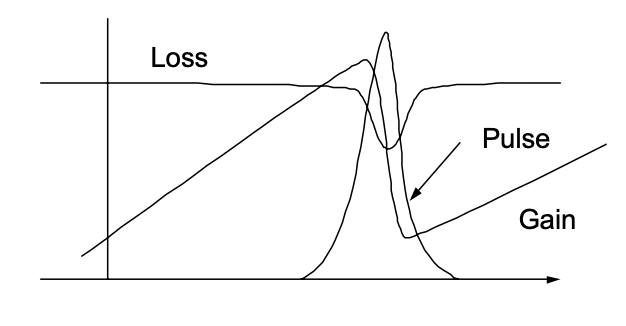
Тепер ми хочемо показати, що насичуваний поглинач призводить до дестабілізації релаксаційних коливань, що призводять до гігантського імпульсного лазера.
Продовжуємо нашу лазерну модель насиченим поглиначем, як показано на малюнку 4.16
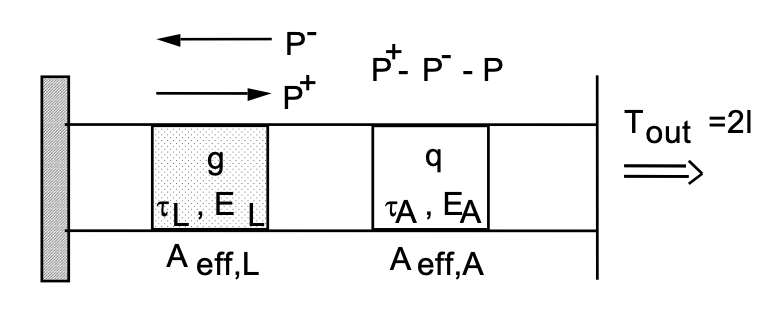
рівняння для лазера з модуляцією добротності
Ми робимо наступні припущення: По-перше, поперечні часи релаксації еквівалентних двох моделей рівня для лазерного середовища посилення і для насичуваного поглинача набагато швидше, ніж будь-яка інша динаміка в нашій системі, так що ми можемо використовувати рівняння швидкості для опису лазерної динаміки. По-друге, ми припускаємо, що зміни інтенсивності лазера, посилення і насичуваного поглинання невеликі за часовою шкалою на порядок часу\(T_R\) в обидва кінці в порожнині, (тобто менше 20%). Потім ми можемо використовувати рівняння швидкості лазера, як виведено вище, плюс відповідне рівняння для насичуваних втрат q, подібне рівнянню для посилення.
\[T_R \dfrac{dP}{dt} = 2(\text{g} - l - q) P\label{eq4.4.18} \]
\[T_R \dfrac{d \text{g}}{dt} = -\dfrac{\text{g} - \text{g}_0}{T_L} - \dfrac{\text{g} T_R P}{E_L} \nonumber \]
\[T_R \dfrac{dq}{dt} = -\dfrac{q -q_0}{T_A} - \dfrac{qT_R P}{E_A}\label{eq4.4.20} \]
де\(P\) позначає потужність лазера,\(\text{g}\) посилення амплітуди в обидва кінці,\(l\) лінійні втрати амплітуди в обидва кінці,\(\text{g}_0\) невеликий коефіцієнт посилення сигналу в обидва кінці і q0 ненасичені, але насичені втрати в обидва кінці. Величини\(T_L = \tau_L/T_R\) і\(T_A = \tau_A/T_R\) є нормованим верхнім станом життя- час середовища посилення і час відновлення абсорбера, нормалізоване до зворотного часу порожнини. Енергії\(E_L = h \nu A_{eff,L}/2^*\sigma_L\) і\(E_A = h \nu A_{eff,A}/2^*\sigma_A\) є енергіями насичення посилення і поглинача відповідно.
Для твердотільних лазерів з коефіцієнтом посилення часу релаксації на порядку\(\tau_L \approx 100 \mu s\) або більше, і порожнини в обидва кінці разів\(T_R \approx 10\) нс, отримаємо\(T_L \approx 10^4\). Крім того, ми припускаємо абсорбери з часом відновлення набагато коротше, ніж час зворотного ходу порожнини, тобто\(\tau_A \approx 1 - 100\) ps, так що, як правило,\(T_A ≈ 10^{-4}\) до\(10^{-2}\). Це досяжно в напівпровідниках і може бути сконструйовано за бажанням завдяки низькому зростанню температури напівпровідникового матеріалу [20, 30]. Поки лазер працює cw і одиночний режим, поглинач буде слідувати миттєвій потужності лазера. Потім насичуване поглинання може бути адіабатично усунуто, використовуючи еквалайзер. (\(\ref{eq4.4.20}\))
\[q = \dfrac{q_0}{1 + P/P_A} \text{ with } P_A = \dfrac{E_A}{\tau_A}, \nonumber \]
і зворотна заміна в еквалайзер. (\(\ref{eq4.4.18}\)). Тут\(P_A\) знаходиться потужність насичення абсорбера. При певній кількості насиченого поглинання коливання релаксації стають нестабільними і відбувається Q-перемикання. Щоб знайти критерій стійкості, лінеаризуємо систему
\[T_R \dfrac{dR}{dt} = (\text{g} - l -q(P))P \nonumber \]
\[T_R \dfrac{d\text{g}}{dt} = -\dfrac{\text{g} - \text{g}_0}{T_L} - \dfrac{\text{g} T_R P}{E_L}. \nonumber \]
Стаціонарне рішення
Як і у випадку з лазером, що працює cw, стаціонарна точка роботи лазера визначається точкою нульового чистого посилення.
\[\begin{array} {rcl} {\text{g}_s} & = & {l + q_s} \\ {\dfrac{\text{g}_0}{1 + P_s/P_L}} & = & {l + \dfrac{q_0}{1 + P_s/P_A}.} \end{array}\label{eq4.4.24} \]
Графічне рішення цього рівняння показано на малюнку 4.17
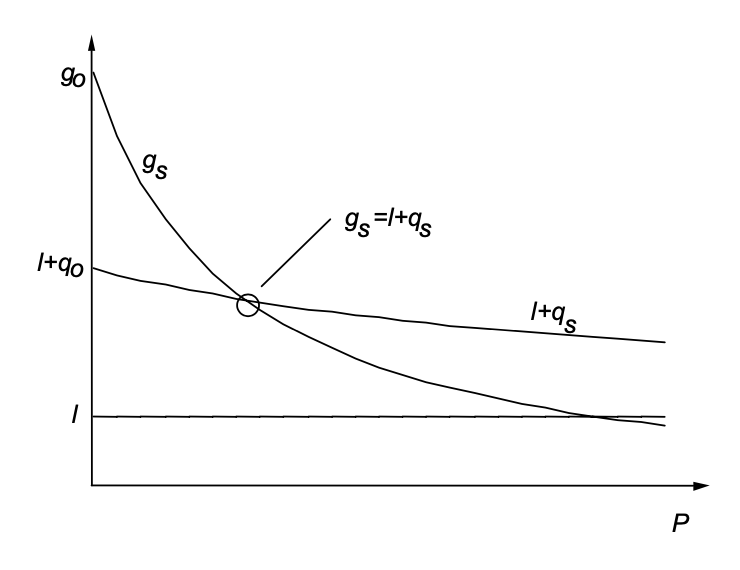
Стабільність стаціонарної робочої точки або умова Q-комутації
Для лінеаризованої системи використовується матриця коефіцієнтів, що відповідає Eq. (4.3.6) змінюється тільки насиченим поглиначем [23]:
\[T_R \dfrac{d}{dt} \left (\begin{matrix} \Delta P_0 \\ Delta \text{g}_0 \end{matrix} \right ) = A \left (\begin{matrix} \Delta P_0 \\ Delta \text{g}_0 \end{matrix} \right ), \text{ with } A = \left (\begin{matrix} -2 \dfrac{dq}{dP}|_{cw} P_s & 2P_s \\ -\tfrac{gsT_R}{E_L} & -\tfrac{T_R}{\tau_{stim}} \end{matrix} \right )\label{eq4.4.25} \]
Матриця\(A\) коефіцієнтів має власні значення з від'ємною дійсною частиною, тоді і лише тоді, коли її слід негативний, а детермінант позитивний, що призводить до двох умов.
\[-2P \dfrac{dq}{dP}|_{cw} < \dfrac{r}{T_L} \text{ with } r = 1 + \dfrac{P_A}{P_L} \text{ and } P_L = \dfrac{E_L}{\tau_L},\label{eq4.4.26} \]
і
\[\dfrac{dq}{dP}|_{cw} \dfrac{r}{T_L} + 2 \text{g}_s \dfrac{r - 1}{T_L} > 0. \nonumber \]
Після скасування\(T_L\) ми закінчуємо
\[\left |\dfrac{dq}{dP} \right |_{cw} < \left |\dfrac{d\text{g}_s}{dP} \right |_{cw}\label{eq4.4.28} \]
Для лазера, який починає коливатися самостійно, співвідношення автоматично\(\ref{eq4.4.28}\) виконується, оскільки мале посилення сигналу більше, ніж загальні втрати, див. Рисунок 4.17. Нерівність (\(\ref{eq4.4.26}\)) має просте фізичне пояснення. Права сторона (\(\ref{eq4.4.26}\)) - це час релаксації посилення до рівноваги, при заданій потужності насоса і постійної потужності лазера. Ліва сторона - це час розпаду коливання потужності лазера при фіксованому коефіцієнті посилення. Якщо посилення не може досить швидко реагувати на коливання потужності лазера, коливання релаксації зростають і призводять до пасивного Q-перемикання лазера.
Як видно з Eq. \(\ref{eq4.4.24}\)і Eq. (\(\ref{eq4.4.26}\)), отримуємо
\[-2T_L P \dfrac{dq}{dP}|_{cw} = 2T_L q_0 \dfrac{\tfrac{P}{\chi P_L}}{(1 + \tfrac{P}{\chi P_L})^2}|_{cw} < r_s \text{ with } \chi = \dfrac{P_A}{P_L},\label{eq4.4.29} \]
де\(\chi\) ефективна «жорсткість» абсорбера проти cw насичення. Співвідношення стійкості\(\ref{eq4.4.29}\) візуалізовано на малюнку 4.18.
Зображення видалено через обмеження авторських прав. Будь ласка, дивіться: Кертнер, Франц та ін. «Контроль твердотільної лазерної динаміки напівпровідниковими приладами». Оптична техніка 34, № 7 (липень 1995): 2024-2036.
Малюнок 4.18: Графічне зображення співвідношення стабільності перемикання CW-Q-для різних продуктів\(2q_0T_L\). Cw-жорсткість, яка використовується для ділянок, є\(\chi = 100\).
Тенденція лазера до Q-перемикача збільшується разом з продуктом\(q_0T_L\) і зменшується, якщо насичуваний поглинач важко насичувати, т\(\chi \gg 1\). Як можна зробити висновок з малюнка 4.18 і ур. (\(\ref{eq4.4.26}\)), лазер ніколи не може Q-перемикач, тобто ліва сторона еквалайзера. (\(\ref{eq4.4.26}\)) завжди менше правого боку, якщо кількість
\[MDF = \dfrac{2q_0T_L}{\chi} < 1\label{eq4.4.27} \]
менше 1. Абревіатура MDF розшифровується як режим блокування рушійної сили, незважаючи на те, що вираз (\(\ref{eq4.4.27}\)) регулює нестабільність Q-комутації. У наступному розділі ми побачимо зв'язок цього параметра з блокуванням режиму. Для твердотільних лазерів з тривалим часом життя верхнього стану, вже дуже малі кількості насичуваного поглинання, навіть частки відсотка, може призвести до досить великого режиму блокування рушійної сили для приведення лазера в Q-перемикання. На малюнку 4.19 показані області в площині\(\chi\) −\(P/P_L\) -, де може відбуватися Q-перемикання для фіксованого МДФ відповідно до відношення (\(\ref{eq4.4.26}\)). Область вище відповідного MDF-значення є областю Q-комутації. Для МДФ <1 CW-Q-перемикання не може відбуватися. Таким чином, якщо має бути спроектований лазер з комутацією CW-Q, потрібно вибрати поглинач з МДФ>1. Чим далі робоча точка розташована в області комутації CW-Q-тим більш вираженою буде CW-Q-комутація. Щоб зрозуміти природу нестабільності, розглянемо власний розв'язок і власні значення лінеаризованих рівнянь руху.\(\ref{eq4.4.25}\)
Зображення видалено через обмеження авторських прав. Будь ласка, дивіться: Кертнер, Франц та ін. «Контроль твердотільної лазерної динаміки напівпровідниковими приладами». Оптична техніка 34, № 7 (липень 1995): 2024-2036.
Малюнок 4.19: При заданому значенні МДФ CW-Q-перемикання відбувається в області над відповідною кривою. Для MDF-значення менше 1 CW-Qперемикання відбуватися не може.
\[\dfrac{d}{dt} \left (\begin{matrix} \Delta P_0 (t) \\ \Delta g_0 (t) \end{matrix} \right ) = s \left (\begin{matrix} \Delta P_0 (t) \\ \Delta g_0 (t) \end{matrix} \right ) \nonumber \]
що призводить до власних значень
\[sT_R = \dfrac{A_{11} + A_{22}}{2} \pm j \sqrt{A_{11}A_{22} - A_{12}A_{21} - \left ( \dfrac{A_{11} + A_{22}}{2} \right )^2}. \nonumber \]
З елементами матриці відповідно до ур. (\(\ref{eq4.4.25}\)) отримуємо
\[s = \dfrac{-\tfrac{2}{T_R} \tfrac{dq}{dP}|_{cw} P_s - \tfrac{1}{\tau_{stim}}}{2} \pm j \omega_Q \nonumber \]
\[\omega_Q = \sqrt{-\dfrac{2}{T_R} \dfrac{dq}{dP}|_{cw} P_s \dfrac{r}{\tau_L} + \dfrac{r - 1}{\tau_p \tau_L} - \left (\dfrac{-\tfrac{2}{T_R} \tfrac{dq}{dP}|_{cw} P_s - \tfrac{1}{\tau_{stim}}}{2} \right )^2} \nonumber \]
де параметр насоса тепер визначається як відношення між малим посиленням сигналу сумарними втратами в сталому стані, т\(r = g_0/(l + q_s)\). Це кілька тривалий вираз наочно показує, що коли система стає нестабільною\(-2\dfrac{dq}{dP} |_{cw} P_s > \dfrac{T_R}{\tau_{stim}}\), при\(\tau_L \gg \tau_p\), відбувається наростаюче коливання з частотою
\[\omega_Q \approx \dfrac{r - 1}{\tau_p \tau_L} \approx \dfrac{1}{\tau_p \tau_{stim}}. \nonumber \]
Тобто пасивне Q-перемикання можна розуміти як дестабілізацію релаксаційних коливань лазера. Якщо система лише трохи перебуває в нестабільному режимі, частота коливань Q-перемикання близька до частоти коливань релаксації. Якщо визначити швидкість росту\(\gamma_Q\), введену насичуваним абсорбером як параметр, власні значення можна записати як
\[s = \dfrac{1}{2} \left ( \gamma_Q - \dfrac{1}{\tau_{stim}} \right ) \pm j \sqrt{\gamma_Q \dfrac{r}{\tau_L} + \dfrac{r - 1}{\tau_p \tau_L} - \left (\dfrac{\gamma_Q - \tfrac{1}{\tau_{stim}}{2} \right )^2}. \nonumber \]
На малюнку 4.20 показана ділянка кореневого локусу для системи з поглиначем та без нього. Насичений поглинач дестабілізує коливання релаксації. Тип біфуркації називається біфуркацією Хопфа і призводить до коливання.
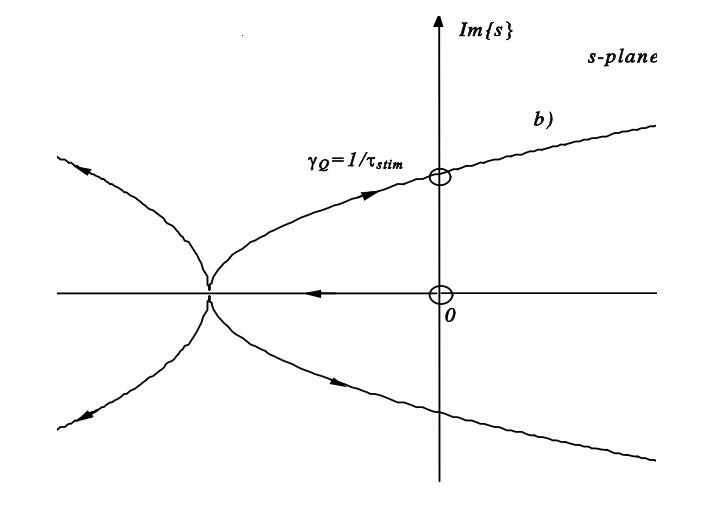
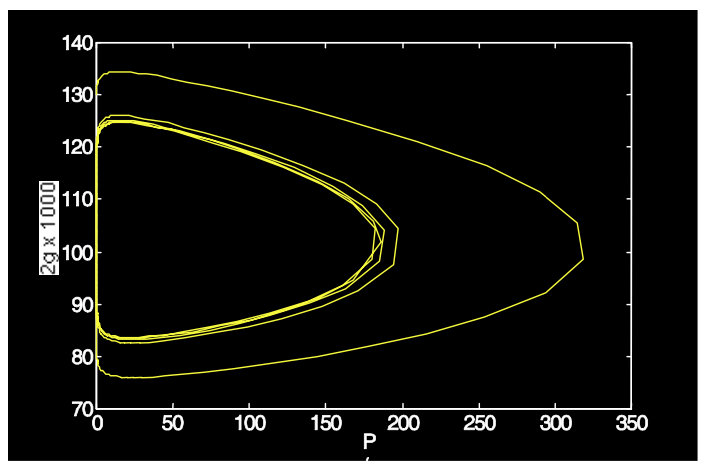
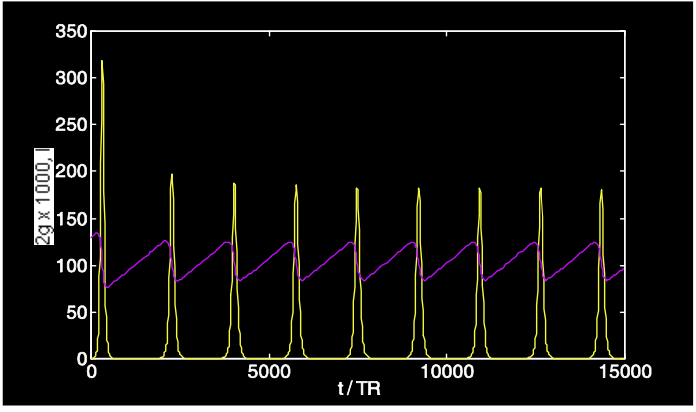
Як приклад розглянемо лазер з наступними параметрами:\(\tau_L = 250 \mu s\),,\(T_R = 4ns\)\(2l_0 = 0.1\),\(2q_0 = 0.005\),\(2g_0 = 2\),\(P_L/P_A = 100\). Рівняння швидкості розв'язуються числово і показані на малюнках4.21 і 4.22.