3.7: Стиснення імпульсів

Поки ми обговорювали поширення імпульсу в негативних дисперсійних середовищах і позитивну самофазову модуляцію. Тоді при досить великій енергії імпульсу може утворитися солітон, оскільки низькочастотні та високочастотні компоненти, що генеруються SPM спереду та ззаду імпульсу, повільні та швидкі і тому наздоганяють пульс і залишаються разом. Що станеться, якщо дисперсія позитивна? Зрозуміло, що низькі та високочастотні компоненти, що генеруються SPM спереду та ззаду імпульсу, швидкі та повільні і безперервно відходять від імпульсу. Це призводить до сильно, але лінійно щебетання імпульсу, який може бути стиснутий після нелінійного поширення, посилаючи його через лінійне негативне дисперсійне середовище або пару призми або пару решіток. Таким чином, імпульси можуть бути стиснуті великими факторами від 3 до 20. Цей процес стиснення імпульсів можна сформулювати більш загальним способом.

Загальна схема компресії імпульсів

Загальна схема імпульсного стиснення оптичних імпульсів була самостійно запропонована Гіресом і Турнуа в 1964 році [38] і Giordmaine et al. в 1968 році [39]. Вхідний імпульс спочатку спектрально розширюється фазовим модулятором. Фаза над генерується спектром, сподіваємось, у формі, яку можна зручно видалити згодом, тобто всі спектральні компоненти можуть бути перефазовані, щоб генерувати короткий імпульс у часовій області. Для стиснення фемтосекундних імпульсів повинен бути використаний надшвидкий фазовий модулятор, тобто імпульс повинен модулювати саму фазу самофазовою модуляцією. У 1969 р\(et\ al\). Фішер. [40] запропонував, що пікосекундні імпульси можуть бути стиснуті до фемтосекундної тривалості за допомогою великого позитивного чирпа, що утворюється навколо піку короткого імпульсу SPM в оптичній рідині Керра. У тому ж році Laubereau [41] використовував кілька осередків, що містять\(\ce{CS2}\) і пару дифракційних решіток, для стиснення приблизно в десять разів 20-ps імпульсів, що генеруються лазером Nd: Glass, що блокується режимом.

Як обговорювалося в розділі 3.2, оптичний ефект Керра в середовищі породжує залежну від інтенсивності зміну показника заломлення\(\Delta n = n_{2,L} I(t)\), де\(n_{2,L}\) коефіцієнт нелінійного показника і\(I(t)\) оптична інтенсивність. Самоіндукований від інтенсивності нелінійний фазовий зсув, що відчувається оптичним полем під час його поширення в середовищі Керра довжини,\(\ell\)\(\omega_0\) задається тим,\(\Delta \phi (t) = -(\omega_0/c)n_2I(t)\ell\) де знаходиться несуча частота імпульсу. Індуковану розгортку частоти над імпульсом можна обчислити з\(\Delta \omega = d \Delta \phi/dt\), див. Малюнок 3.13. Навколо центральної частини імпульсу, де зосереджена велика частина енергії, фаза параболічна, що призводить до приблизно лінійного щебетання по частоті. Область з лінійним щебетанням може бути збільшена за наявності позитивної дисперсії в середовищі Керра того ж знака [42]. Для стиснення спектрально розширеного і щебетання імпульсу може бути використана дисперсійна лінія затримки, що характеризується майже лінійною груповою затримкою\(T_g(\omega)\). Або якщо щебетання, що генерується над новоствореним спектром, є нелінійним, цей чірп повинен бути видалений відповідно нелінійною груповою затримкою\(T_g(\omega)\). На малюнку 3.13 видно, що в разі SPM і позитивного GDD створюється більш плавний спектр з більш лінійним чирпом і тому кінцевий стиснутий імпульс більш високої якості, тобто більший відсоток загальної енергії імпульсу дійсно зосереджений в короткому імпульсі, а не у великому нестиснутому імпульсному п'єдесталі.

Малюнок 3.13: Профіль інтенсивності, спектр, миттєва частота, оптимальне квадратичне стиснення та ідеальне стиснення для двох випадків: верхній ряд для короткого волокна, тобто висока нелінійність і низька дисперсія; оптимальна нелінійність і дисперсія нижнього ряду [42] Накацука, Г., Гришковський, Д.Грішковський та А.К. Балант. «Нелінійне поширення пікосекундних імпульсів через оптичні волокна з позитивною груповою дисперсією швидкостей.» Листи огляду фізики 47 (1981): 910-913.

Для променя, що поширюється в однорідному середовищі, на жаль, нелінійний показник заломлення призводить не тільки до тимчасової фазової модуляції, але і до просторової фазової модуляції, що призводить до самофокусування або розфокусування і маломасштабної нестабільності [43]. Тому фундаментальною вимогою до компресії імпульсів є те, що ефект Керра забезпечується направляючим нелінійним середовищем, щоб отримати просторово рівномірне спектральне розширення. У 1974 році\(et\ al\) Іппен. повідомив про перше вимірювання SPM при відсутності самоуловлювання і самофокусування за допомогою направляючого багатомодового оптичного волокна, наповненого рідиною\(\ce{CS2}\) [44]. У 1978 році Stolen and Lin повідомили про вимірювання SPM в одномодових волокні кремнезему ядра [45]. Важливою перевагою одномодового волокна є те, що фазову модуляцію можна накладати по всьому поперечному профілю променя, тим самим усуваючи проблему немодульованого світла в крилах променя [44]. У 1981 р. Накацука\(et\ al\). [42] виконав перший експеримент зі стисненням імпульсів, використовуючи волокна як середовище Керра в області позитивної дисперсії.

Спектральне розширення з керованими режимами

Електричне поле керованого режиму можна записати як [52]:

\[E(\text{r}, \omega) = A(z, \omega) F(x, y) \exp [i \beta (\omega) z] \nonumber \]

де\(A(z, \omega)\) - мод-амплітуда для заданої частотної складової,\(F(x, y)\) - це режим поперечного розподілу поля і\(\beta (\omega)\) постійна мода-поширення. Рівняння поширення для керованого поля розбивається на два рівняння для амплітуди\(A(z, \omega)\) та картини поля\(F(x,y)\). У теорії збурень першого порядку\(\Delta n = \bar{n}_2 |E|^2\) збуренням показника заломлення, який набагато менше, ніж крок індексу, що визначає режим, не змінює модальний розподіл\(F(x,y)\), тоді як константа поширення мод\(\beta (\omega)\) може бути записана як\(\bar{\beta} (\omega) = \beta (\omega) + \Delta \beta\), де збуреність \(\Delta \beta\)дається

\[\Delta \beta = \dfrac{(\omega_0/c) \displaystyle \iint \Delta n |F(x, y)|^2 dx\,dy}{\displaystyle \iint |F(x, y)|^2 dx\,dy}.\label{eq3.7.2} \]

Як показав Eq. (\(\ref{eq3.7.2}\)), збуренням\(\Delta \beta\), яке включає ефект, обумовлений нелінійністю волокна, пов'язане з просторовим середнім на волоконно-транс-віршованому перерізі збурень\(\Delta n\). Таким чином реалізується просторово рівномірний SPM.

Малюнок 3.14: Волоконно-гратчастий імпульсний компресор для генерації фемтосекундних імпульсів [53]. Малюнок MIT OCW.

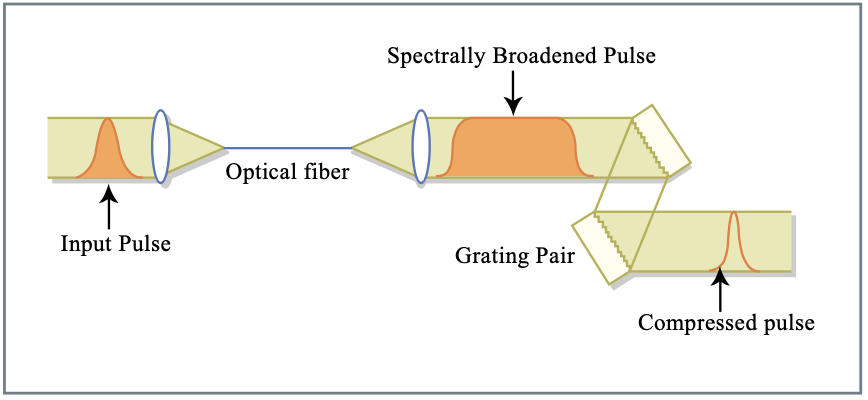
Використовуючи звичайні одномодові волокна і призма-гратчасті компресори, імпульси коротше 6 фс при 620 нм були отримані в 1987 році з імпульсів 50 фс, що генеруються зіткненно-імпульсним режимом блокування лазером барвника [46] див. Рис. 3.14. Зовсім недавно 13-fs імпульси з порожнино-скинутого Ti:Sapphire лазера були стиснуті до 4,5 фс за тією ж методикою за допомогою компресора, що складається з кварцової 45\(^{\circ}\) - призматичної пари, широкосмугових щебетаних дзеркал і тонкоплівкових діелектричних інтерферометрів Жира-Турнуа [47, 54]. Використання одномодового оптичного волокна обмежує енергію імпульсу до декількох наноджоулей.

У 1996 році за допомогою фазового модулятора, що складається з порожнистого волокна (дірявого хвилеводу), заповненого благородним газом, була введена потужна методика компресії імпульсів, яка обробляє імпульси високої енергії [48]. Реалізація методики стиснення порожнистих волокон з використанням 20-fs насіннєвих імпульсів із системи Ti:Sapphire та дзеркальних дзеркал, що утворюють дисперсійну лінію затримки, призвела до генерації імпульсів тривалістю до 4,5 фс [49] та енергією до 0,55 мДж [50]. Дана методика представляє переваги направляючого елемента з режимом великого діаметра та швидкого нелінійного середовища з високим порогом пошкодження.

Можливість скористатися ультраширокосмуговим спектром, який може бути створений процесом фазової модуляції, суворо пов'язана з розвитком дисперсійних ліній затримки, здатних контролювати частотно-залежну групову затримку над такою смугою пропускання.

Методи компенсації дисперсії

Частотна розгортка імпульсів (щебетання), накладена фазовою модуляцією, приблизно лінійна поблизу піку імпульсу, де зосереджена велика частина енергії. При наявності дисперсії в фазовому модуляторі щебетання стає лінійним майже по всьому імпульсу. Тому оптимальне тимчасове стиснення вимагає групової затримки\(T_{g,comp} (\omega) = \partial \phi /\partial \omega\), що характеризується майже лінійною залежністю від частоти в дисперсійній лінії затримки. Оскільки у випадку SPM нелінійний індекс\(n_2\), як правило, позитивний далеко від резонансу, в компресорі потрібна негативна групова затримка дисперсії (\(GDD = \partial T_g/\partial \omega\)). Для того, щоб генерувати найкоротші імпульси, затримка групи імпульсів після фазового модулятора та компресора повинна бути майже незалежною від частоти. \(T_g(\omega)\)можна розширити в серію Тейлора навколо центральної частоти\(\omega_0\):

\[T_g (\omega) = \phi' (\omega_0) + \phi'' (\omega_0) \Delta \omega + \dfrac{1}{2} \phi ''' (\omega_0) \Delta \omega^2 + \dfrac{1}{3!} \phi '''' (\omega_0) \Delta \omega^2 + \cdots \label{eq3.7.3} \]

де\(\Delta \omega = \omega - \omega_0\), і\(\phi '' (\omega_0)\)\(\phi ''' (\omega_0)\), і\(\phi '''' (\omega_0)\) є другим-, третім-, і четвертим порядком-дисперсійним термінами відповідно. Критичні значення цих термінів дисперсії, над якими дисперсія викликає значну зміну імпульсу, задаються простим\(\phi^{(n)}\) масштабувальним виразом:\(\phi^{(n)} = \tau_p^n\), де термін дисперсії n-го порядку і\(\tau_p\) тривалість імпульсу. Наприклад, дисперсія другого порядку з\(\phi '' = \tau_p^2\) призводить до розширення імпульсу більш ніж в два рази. Тому розширення та спотворення імпульсів, індуковане дисперсією, стають все більш важливими для зменшення тривалості імпульсу. Рівняння (\(\ref{eq3.7.3}\)) показує, що для стиснення імпульсу до межі перетворення слід усунути ці члени дисперсії високого порядку. Наприклад, припускаючи, що вхідний імпульс з обмеженим перетворенням до фазового модулятора, умовою стиснення з компенсацією дисперсії третього порядку є наступним:

\[\phi '' (\omega_0) = \phi''_{modulator} + \phi''_{compresssor} = 0 \nonumber \]

\[\phi ''' (\omega_0) = \phi'''_{modulator} + \phi'''_{compresssor} = 0 \nonumber \]

До теперішнього часу розроблено кілька компресорних схем, які включали в себе такі компоненти, як: дифракційні решітки, пари призми, вирізані Брюстера, поєднання решіток і призм, тонкі призми і щебетання дзеркал, а також тільки дзвін дзеркал і т.д. далі ми коротко викладемо основні характеристики цих компресорні схеми.

Пари решітки та призми

У 1968 році Трейсі вперше продемонструвала використання пари дифракційних решіток для досягнення негативного ГДД [55]. У 1984 році Fork et al. отримали негативний GDD з парами кутових призм Брюстера [56]. Пари призми широко використовуються для управління дисперсією всередині лазерних генераторів, оскільки вони можуть бути дуже низькими втратами на відміну від гратчастих пар. В обох оптичних системах походженням регульованої дисперсії є кутова дисперсія, яка виникає внаслідок дифракції та заломлення відповідно. Введену цими системами дисперсію можна легко розрахувати, обчисливши фазу, накопичену між вхідною і вихідною опорними площинами [78]. Щоб зрозуміти основні властивості цих систем, ми звернемося до малюнка 3.15.

Малюнок 3.15: Оптична різниця шляху в двоелементній дисперсійній лінії затримки [107] Рисунок MIT OCW.

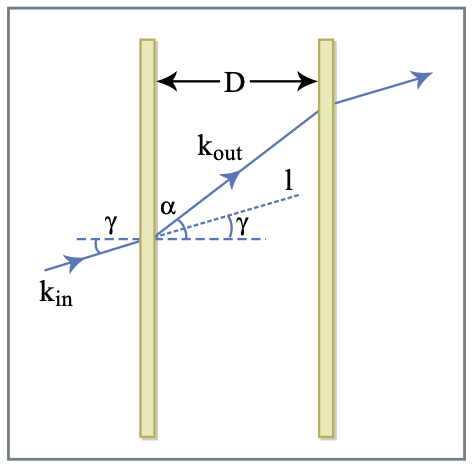
Перший елемент розсіює вхідний промінь з хвильовим вектором\(\text{k}_{in}\) і вектор вхідного шляху\(\text{l}\) в напрямку\(\text{k}_{out}\). Промінь проходить між першим і другим елементом і розкидається назад в початковому напрямку. Різниця фаз розсіяним променем і опорним пучком без решітки становить:\(\phi (\omega) = \text{k}_{out} (\omega) \cdot \text{l}\). Розглядаючи поширення вільного простору між двома елементами, ми маємо\(|\text{k}_{out}| = \omega/c\), і накопичену фазу можна записати як

\[\phi (\omega) = \dfrac{\omega}{c} |\text{l}| \cos [\gamma - \alpha (\omega)] = \dfrac{\omega}{c} \dfrac{D}{\cos (\gamma)} \cos [\gamma -\alpha (\omega)]\label{eq3.7.6} \]

де:\(\gamma\) кут між вектором падаючої хвилі і нормаллю до першого елемента;\(\alpha\) кут вектора вихідної хвилі, який є функцією частоти;\(D\) - інтервал між елементами розсіювання по напрямку, паралельному їх нормалі. У випадку гратчастої пари залежність кута дифракції\(α\) регулюється законом решітки, який у випадку дифракції першого порядку задається:

\[\dfrac{2\pi c}{omega} = d[\sin \alpha (\omega) - \sin \gamma]\label{eq3.7.7} \]

де\(d\) - відстань між канавками решітки. Використання Eq. (\(\ref{eq3.7.6}\)) і Eq. (\(\ref{eq3.7.7}\)), можна отримати аналітичні вирази для GDD та термінів дисперсії вищого порядку (для одного проходу):

\[\phi '' (\omega) = -\dfrac{4\pi^2 cD}{\omega^3 d^2 \cos^3 \alpha (\omega)}\label{eq3.7.8} \]

\[\phi ''' (\omega) = \dfrac{12 \pi^2 cD}{\omega^4 d^2 \cos^3 \alpha (\omega)} \left (1 + \dfrac{2 \pi c \sin \alpha (\omega)}{\omega d \cos^2 \alpha (\omega)} \right ) \nonumber \]

Це видно з Eq. (\(\ref{eq3.7.8}\)) що пари решіток дають негативну дисперсію. \(D\)це відстань між гратами. Недоліком решітчастої пари є дифракційні втрати. Для конфігурації з подвійним проходом втрата зазвичай становить 75%. Також обмежена пропускна здатність для ефективної дифракції.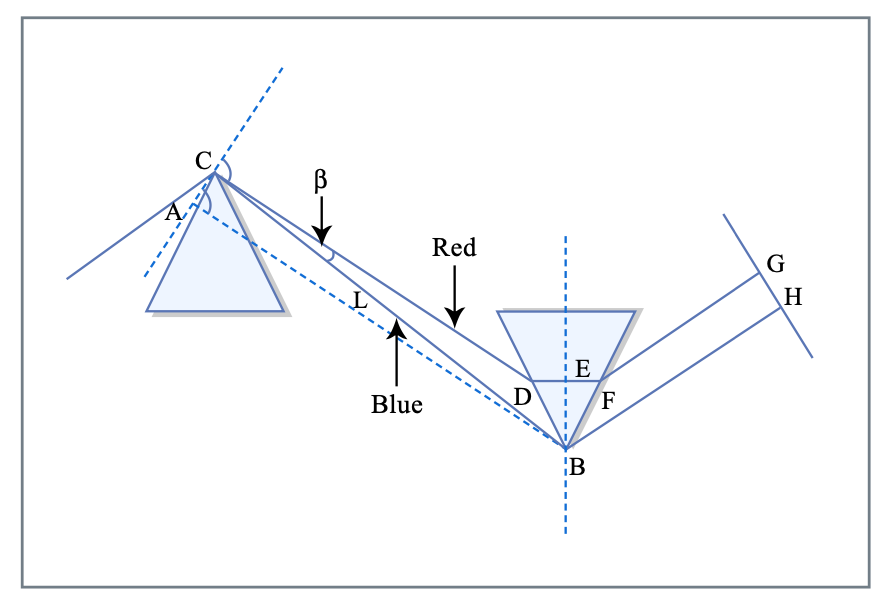
Малюнок 3.16: Пара призми для компенсації дисперсії. Сині довжини хвиль мають менше матеріалу в світловому шляху, ніж червоні довжини хвиль. Тому сині довжини хвиль менше затримуються, ніж червона довжина хвилі Малюнок MIT OCW.

У випадку з кутовою призмою Брюстера пара Eq. (\(\ref{eq3.7.6}\)) зводиться до наступного виразу (для одного проходу) [56]:

\[\phi (\omega) = \dfrac{\omega}{c} \ell_p \cos \beta (\omega) \nonumber \]

де\(\ell_p\) - відстань між вершинами призми і\(\beta (\omega)\) кут між заломленим променем на\(\omega\) частоті і лінією, що з'єднує дві верхівки. Дисперсія другого і третього порядку може бути виражена через оптичний шлях\(P(\lambda) = \ell_p \cos \beta (\lambda)\):

\[\phi '' (\omega) = \dfrac{\lambda^3}{2\pi c^2} \dfrac{d^2 P}{d\lambda^2} \nonumber \]

\[\phi ''' (\omega) = - \dfrac{\lambda^4}{4 \pi^2 c^3} \left ( 3 \dfrac{d^2 P}{d \lambda^2} + \lambda \dfrac{d^3 P}{d \lambda^3} \right ) \nonumber \]

з наступними похідними оптичного шляху щодо довжини хвилі, оціненої під кутом Брюстера:

\[\dfrac{d^2 P}{d\lambda^2} = 2[n'' + (2n - n^{-3})(n')^2] \ell_p \sin \beta - 4(n')^2 \ell_p \cos \beta \nonumber \]

\[\dfrac{d^3 P}{d \lambda^3} = [6(n')^3 (n^{-6} + n^{-4} - 2n^{-2} + 4n^2) + 12n'n''(2n - n^{-3}) + \nonumber \]

\[+ 2n'''] \ell_p \sin \beta + 12[(n^{-3} -2n)(n')^3 - n'n''] \ell_p \cos \beta \nonumber \]

де\(n\) - показник заломлення матеріалу призми;\(n'\),\(n''\) і\(n'''\) є відповідно похідними першого, другого і третього порядку\(n\), по відношенню до довжини хвилі. Призма-компресор має перевагу в зменшенні втрат. Використовуючи лише призми плавленого кремнезему для компенсації дисперсії, світлові імпульси суб-10-fs були створені безпосередньо з генератора в 1994 році [79]. У 1996 році імпульси з енергією десятків мікроджоулів, спектрально розширені в газонаповненому порожнистому волокні, були стиснуті до 10 фс за допомогою призмного компресора [48]. Як у випадку гратчастої пари, так і призми, негативний GDD пов'язаний зі значною кількістю дисперсії вищого порядку, яка не може бути знижена або відрегульована незалежно від бажаного GDD, тим самим обмежуючи пропускну здатність, над якою можна отримати правильний контроль дисперсії. Цей недолік був подоланий лише частково, поєднуючи пари призми та решітки з дисперсією третього порядку протилежного знака. Таким чином імпульси, короткі, як 6 фс, були сформовані в 1987 році [46], і менше 5 фс в 1997 році [47], шляхом зовнішнього стиснення. Ця комбінація не може бути використана для генерації імпульсів з малим оптичним циклом ні в лазерних генераторах через високі дифракційні втрати решіток, ні в зовнішніх компресорах на високому рівні потужності, через виникнення небажаних нелінійностей в призмах.

Дисперсійні компенсаційні дзеркала

Щебетані дзеркала використовуються для стиснення імпульсів високої енергії, оскільки вони забезпечують високу дисперсію з невеликою кількістю матеріалу на шляху променя, тим самим уникаючи нелінійних ефектів в компресорі.

Решітка і призма компресори страждають від більш високого порядку дисперсії. У 1993 році Роберт Шипеч і Ференц Крауш [80] придумали нову ідею, так звану щебетання дзеркал. Лазерні дзеркала - це діелектричні дзеркала, що складаються з змінних товстих шарів з високим та низьким показником чверті довжини хвилі, що призводить до сильного відбиття У щебетаних дзеркалах довжина хвилі Брегга щебетати так, що різна довжина хвилі проникає різною глибиною в дзеркало при відображенні, що породжує залежну від довжини хвилі групову затримку. Виявляється, генерація малоциклових імпульсів за допомогою зовнішнього стиснення [95], а також пряма генерація з лазерів з блокуванням режиму лінзи Керра [58] в значній мірі спирається на існування щебетаних дзеркал [57, 83, 59] для компенсації дисперсії. Є дві причини використовувати щебетання дзеркал. Спочатку смуга пропускання високої відбивної здатності стандартного діелектричного дзеркала Брагга визначається відбивною здатністю\(r_B\) Френеля високих і низьких індексних матеріалів\(n_L\), що використовуються для діелектричного дзеркала\(\Delta f\)\(n_H\)

\[r_B = \dfrac{\Delta f}{f_c} = \dfrac{n_H - n_L}{n_H + n_L} \nonumber \]

\(f_c\)де знову центральна частота дзеркала. Металеві дзеркала, як правило, занадто втратні, особливо при використанні в якості внутрішньопорожнинних лазерних дзеркал. Для матеріальних систем, які зазвичай використовуються для широкосмугових оптичних покриттів\(n_{\ce{TiO2}} = 2.4\), таких як діоксид кремнію\(n_{\ce{SiO2}} = 1.48\) та діоксид титану з і (ці показники можуть змінюватися залежно від використовуваної техніки осадження),\(\Delta f/f_c = 0.23\) можна покрити дробову смугу пропускання. Ця дробова смуга пропускання становить лише близько третини октави, що охоплює дзеркало\(\Delta f/f_c = 2/3\). Крім того, зміна групової затримки дзеркала Брагга впливає вже на імпульси, які заповнюють половину спектрального діапазону\(\Delta f = 0.23f_c\). Вихід з цієї дилеми був знайдений шляхом введення щебетання дзеркал [57], еквівалент щебетання волокнистих брегговських решіток, які на той момент були вже добре розвиненими компонентами в волоконній оптиці [60]. Коли довжина хвилі Брегга дзеркального стека змінюється досить повільно і не існує обмежень на кількість пар шарів, можна розробити довільний високий діапазон відбивної здатності дзеркала. Друга причина використання щебетаних дзеркал заснована на їх дисперсійних властивостях, обумовлених залежною від довжини хвилі глибини проникнення відбитого від різних положень світла всередині щебетаної багатошарової структури. Дзеркала - це фільтри, і в конструкції будь-якого фільтра контроль групової затримки і групової затримки дисперсії утруднений. Ця проблема ще більше посилюється, коли конструкція повинна працювати в діапазонах довжин хвиль до октави або більше.

проблема узгодження

Малюнок 3.17: а) Стандартне дзеркало Брегга; (б) Просте дзеркальне дзеркало, (в) Подвійне дзеркальне дзеркало з відповідними секціями, щоб уникнути залишкових відбитків, що викликають небажані коливання в GD і GDD дзеркала. Малюнок MIT OCW.

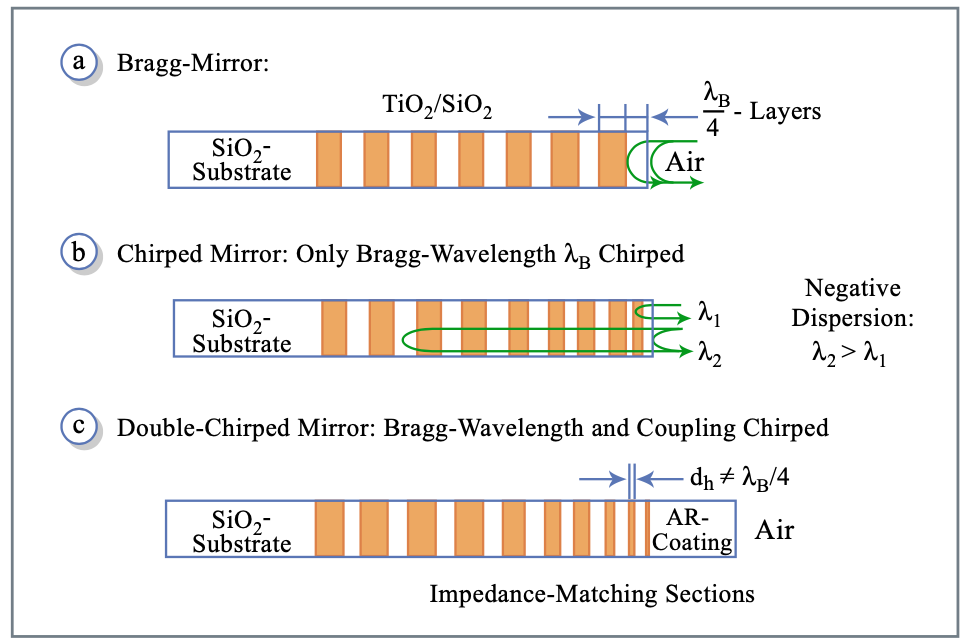
За останні роки було розроблено кілька конструкцій ультра широкосмугових дисперсійних компенсуючих дзеркал. Для дзеркал, що компенсують дисперсію, які не розширюють високий діапазон відбивної здатності далеко за межі того, що вже може досягти дзеркало Брагга, що використовує ті ж матеріали, конструкція фільтра з кількома порожнинами може бути використана для наближення бажаних фазових і амплітудних властивостей [61, 62]. Для компенсації дисперсії дзеркал, що охоплюють високий діапазон відбивної здатності аж до\(\Delta f/f_c = 0.4\) концепції подвійних дзеркальних дзеркал (DCM) [83] [81]. Він заснований на наступних спостереженнях. Просте дзеркальне дзеркало забезпечує високу відбивну здатність у довільному діапазоні довжин хвиль і, в певних межах, призначену для користувача середню групову затримку через глибину проникнення, залежну від довжини хвилі [73] (див. Рис. 3.17 (a) та (b)). Однак групова затримка як функція частоти показує періодичні зміни через невідповідність імпедансу між навколишнім середовищем і дзеркальним стеком, а також всередині стека (див. Рис. 3.17 b і рис. 3.18). Структурою, яка пом'якшує ці розбіжності і дає кращий контроль групової затримки дисперсії (GDD), є подвійне дзеркальне дзеркало (DCM) (рис. 3.17 в), подібним до способу аподированного волокна Брегга решітки [64].

Картнер, Ф.Х., та ін. «Проектування та виготовлення дзеркал з подвійним сколом». Оптика Листи 15 (1990): 326-328.

Малюнок 3.18: Порівняння відбивної здатності і групової затримки щебетаних дзеркал з 25 парами шарів і показниками заломлення\(n_H = 2.5\), і\(n_L = 1.5\). Верхня частина показує збільшений верх на один відсоток відбивної здатності. Пунктирні криві показують результат для простого щебетання дзеркала. Пунктирна і суцільна криві показують результат для подвійних щебетаних дзеркал, де крім щебетання в номері\(k_B\) хвилі Брегга товщина високоіндексних шарів щебетати над першими 12 парами шарів від нуля до його максимального значення для лінійного щебетання\(\alpha = 1\), тобто (пунктирні криві) і для квадратичного щебетання, тобто\(\alpha = 2\) (тверді криві). [83].

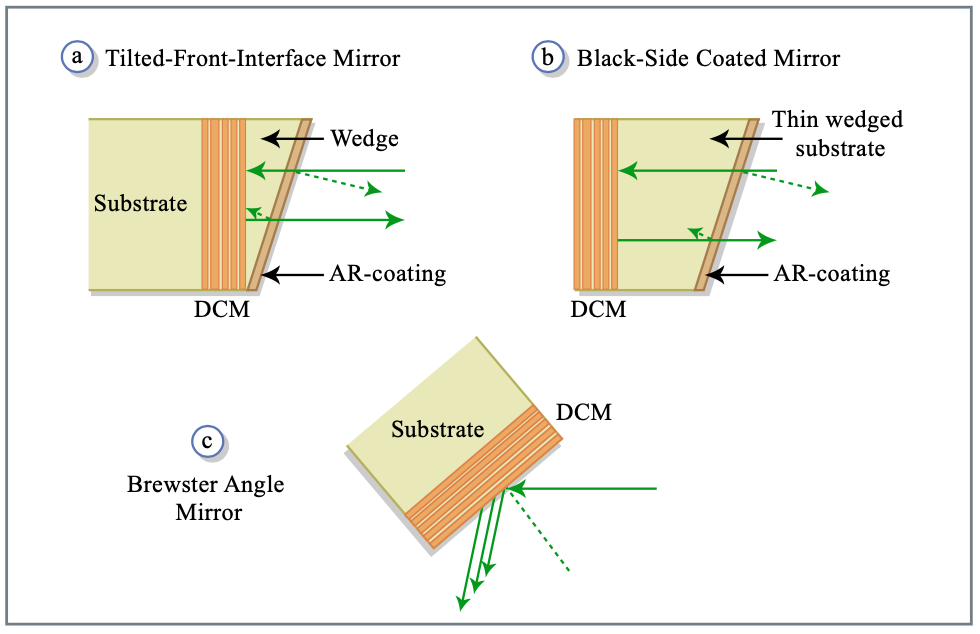
На малюнку 3.18 показана відбивна здатність та групова затримка декількох дзеркал Брегга та щебетання, що складаються з кроків показника 25\(n_L = 1.5\), з\(n_H = 2.5\) і, подібними до показників заломлення\(\ce{TiO2}\) і\(\ce{SiO2}\), які призводять до відбивної здатності Френеля\(r_B = 0.25\). Брагг-дзеркало може бути розкладено симетричними індексними кроками [83]. Хвильове число Брегга визначається як\(k_B = \pi/(n_Ld_L + n_H d_H)\), де\(d_L\) і\(d_H\) є товщиною шару низького та високого індексу відповідно. Хвильове число Брегга описує центральний хвильовийномер дзеркала Брегга, що складається з рівних кроків індексу. У першому випадку (рис. 3.18, штрих-пунктирна лінія) тільки число хвилі Брегга лінійно щебетати від\(6.8 \mu m^{-1} < k_B < 11 \mu m^{-1}\) перших 20 кроків індексу і утримується постійним протягом останніх 5 кроків індексу. Відбивна здатність структури обчислюється припускаючи, що структура вбудована в середовище з низьким індексом. Великі коливання в груповій затримці викликані різними імпедансами щебетання решітки і навколишнього матеріалу з низьким індексом, що викликає сильне відображення на межі розділу матеріалу з низьким індексом і стека решітки. Шляхом адіабатичного узгодження імпедансу решітки з низьким індексом матеріалу цього відбиття можна уникнути. Це продемонстровано на малюнку 3.18 пунктирною і суцільною кривими, що відповідають додатковому щебетання шару високого індексу над першими 12 кроками відповідно до закону\(d_H = (m/12)^{\alpha} \lambda_{B,12}/(4n_H)\) з\(\alpha = 1\), і 2, для лінійного і квадратичного адіабатичного узгодження. Аргумент m позначає м-ий крок індексу і\(\lambda_{B,12} = 0.740\mu m\). Добре видно сильне зменшення коливань в груповій затримці методом подвійного щебетання. Квадратичне звуження шару високого індексу, а отже, решітки вже повністю виключає коливання в груповій затримці, що також може бути показано аналітично методом аналізу зв'язаного режиму [81]. Через подвійне щебетання відкривається вікно високої передачі на короткохвильовому кінці дзеркала, яке ідеально підходить для накачування лазерів Ti: Sapphire. Поки дзеркальне дзеркало з подвійним щебетанням відповідає лише низькому індексу матеріалу дзеркала. В ідеалі відповідність можна розширити на будь-яке інше середовище за допомогою правильно розробленого AR-покриття. Однак це AR-покриття має бути дуже якісним, тобто дуже низькою залишковою відбивною здатністю в ідеалі потужності відбивної здатності\(10^{-4}\),\(r = 10^{-2}\) тобто потрібна амплітудна відбивна здатність. Якість AR-покриття можна послабити, якщо залишкове відображення направлено за межі шляху променя. Це досягається в так званих нахилених дзеркалах з лицьовим або заднім боковим покриттям [65], [66], (рис. 3.19 (а) і (б)). У дзеркалі з задньою стороною ідеальна структура DCM, яка відповідає низькому індексу матеріалу дзеркала, наноситься на зворотну сторону підкладки, виготовленої з того ж або принаймні дуже схожого матеріалу з низьким індексом. AR-покриття наноситься на передню частину злегка клинованої підкладки, завдяки чому залишкове відображення спрямоване з променя і не впливає на дисперсійні властивості. Таким чином, завдання AR-покриття полягає лише в тому, щоб зменшити втрати Френеля дзеркала на межі розділу повітряної підкладки, а отже, воно досить добре для деяких застосувань, якщо залишкове відображення на цьому інтерфейсі становить близько 0,5%. Однак підкладка повинна бути дуже тонкою, щоб зберегти загальну дзеркальну дисперсію негативною, як правило, близько 200-500\(\mu\) м Оптика якості лазера важко зробити на таких тонких підкладках і напруга, викликана покриттям, призводить до небажаної деформації підкладок. Дзеркало з лицьовим покриттям долає цей недолік, осаджуючи ідеальну DCM-структуру, відповідну індексу клинового матеріалу на звичайній підкладці лазерного класу. Тонкий клин 100-200 мкм скріплюється поверх дзеркала, а AR-покриття потім наноситься на цей клин. Це призводить до стабільних і октавних дзеркал, які успішно використовуються в експериментах із зовнішнім стисненням [69]. Обидві конструкції мають обмеження. Спочатку вводять в балку клин, що призводить до небажаного кутового розсіювання пучка. Частково це можна компенсувати, використовуючи ці дзеркала в парі з протилежно орієнтованими клинами. Другий недолік полягає в тому, що, здається, неможливо зробити якісні AR-покриття понад одну або більше однієї октави смуги пропускання, які мають менше 0,5% залишкової відбивної здатності [68], тобто на одному відображенні таке дзеркало має не менше 1% втрат, а, отже, такі дзеркала викликають великі втрати всередині лазера. Для зовнішнього стиснення ці втрати прийнятні. Третя можливість подолання проблеми AR-покриття надається за допомогою ідеального DCM при падінні кута Брюстера, (рис. 3.19) [67]. У цьому випадку шар з низьким індексом автоматично узгоджується з навколишнім повітрям. Однак при p-поляризованому падінні індексний контраст або відбивна здатність Френеля пари шарів зменшується, і для досягнення високої відбивної здатності необхідно більше пар шарів. Також збільшилася глибина проникнення в дзеркало, завдяки чому розсіювання і інші втрати в шарах стають більш вираженими. З іншого боку, таке дзеркало може генерувати більшу дисперсію на відскік через більшу глибину проникнення. Для зовнішнього стиснення такі дзеркала можуть мати переваги, оскільки вони можуть охоплювати смугу пропускання набагато ширше однієї октави. Це поняття важко застосувати до виготовлення криволінійних дзеркал. Існує також просторовий щебетання відбитого променя, який може стати значним для великої глибини проникнення і повинен бути видалений зворотним відображенням або додатковим відскоком на іншому кутовому дзеркалі Брюстера, яке рекомбінує промінь. Для внутрішньопорожнинних дзеркал вихід з цієї дилеми знаходять дзеркальні пари, які скасовують помилкові відбиття через недосконале AR-покриття і відповідну структуру в щебетаному дзеркалі [76]. Також така конструкція має свої недоліки і обмеження. Це вимагає високої точності при виготовленні, і залежно від пропускної здатності дзеркал можна використовувати їх лише для обмеженого діапазону кутів падіння.

Малюнок 3.19: Схематична структура запропонованої широкосмугової дисперсії Compen- sating дзеркальної системи уникаючи відповідності повітрю: (а) нахилене дзеркало переднього інтерфейсу; (б) дзеркало з задньою стороною і (в) дзеркало Брюстера кут.. Малюнок MIT OCW.

Подвійні дзеркальні пари

Малюнок 3.20: DCM-пара M1 (a) і M2 (b). DCM M1 може бути деком- поставлений у подвійному щебетання заднього дзеркала MB, узгодженому з середовищем з індексом самого верхнього шару. У М2 шар з товщиною чверті хвилі на центральній частоті дзеркала і індексом, еквівалентним самому верхньому шару заднього дзеркала MB вставляється між заднім дзеркалом і AR-покриттям. Нове заднє дзеркало, що містить шар чверті хвилі, може бути переоптимізовано для досягнення тієї ж фази, що і MB з додатковим π-фазовим зсувом по всій октаві смуги пропускання.. Малюнок MIT OCW.

Було кілька пропозицій щодо збільшення пропускної здатності лазерних дзеркал шляхом взаємної компенсації коливань GDD [70, 71, 72] за допомогою комп'ютерної оптимізації. Ці ранні дослідження призвели до досить низької відбивної здатності менше 95% протягом майже половини розглянутої пропускної здатності. Ідеї, що ведуть до DCM, допомагають нам аналітично показати, що конструкція DCM-пар, що охоплюють одну октаву смуги пропускання, тобто від 600 нм до 1200 нм, з високою відбивною здатністю і поліпшеними характеристиками дисперсії дійсно можлива [76]. Використання цих дзеркальних пар в лазерній системі Ti:Sapphire призвело до 5 fs імпульсів з октавними спектрами, що охоплюють безпосередньо від лазера [58]. Тим не менш, потенціал цих пар аж ніяк не експлуатується повністю.

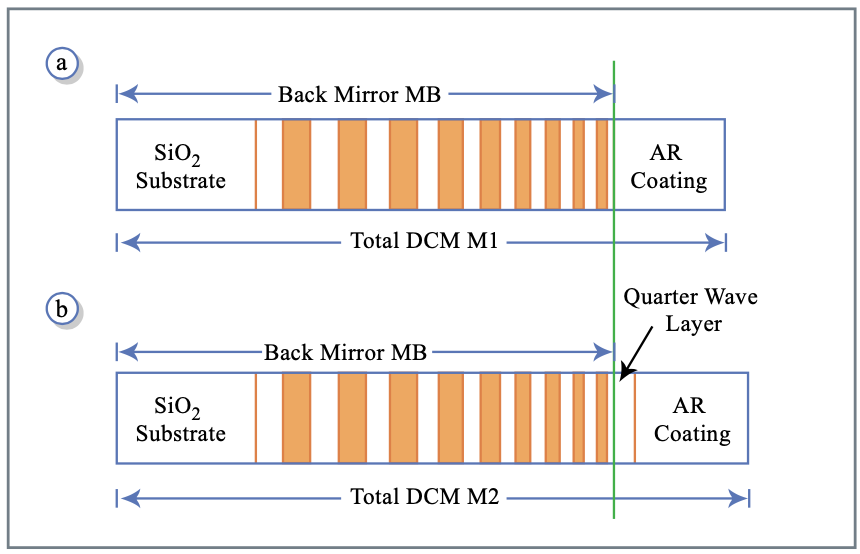
DCM-пара, див. Рис. 3.20, складається з дзеркала М1 і М2. Кожен складається з AR-покриття та відповідного подвійного дзеркального дзеркала з низьким індексом MB із заданою глибиною проникнення залежно від довжини хвилі. Високий діапазон відбивної здатності заднього дзеркала можна легко розширити до однієї октави, просто щебетати досить повільно і використовуючи достатню кількість пар шарів.

Малюнок 3.21: Розкладання DCM на подвійне щебетання заднього дзеркала MB і AR-покриття.. Малюнок MIT OCW.

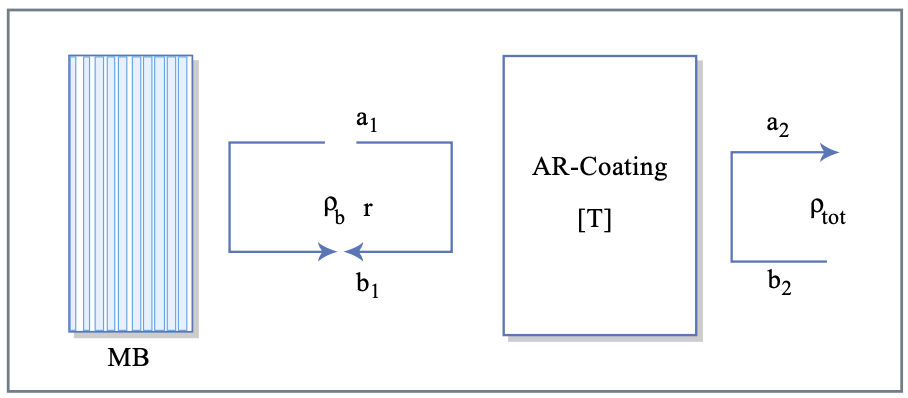
Однак гладкість одержуваного ГДД сильно залежить від якості відповідності, що забезпечується AR-покриттям і подвійним щебенем перетином. Малюнок 3.21 вказує на вплив AR-покриття на ГДД загальної DCM-структури. AR-покриття представлено у вигляді двох - порту з двома вхідними хвилями a1, b2 і двома вихідними хвилями a2, b1. Зв'язок між хвилями лівого порту і правого порту описується матрицею передачі.

\[\left (\begin{matrix} a_1 \\ b_1 \end{matrix} \right ) = T_{ar} \left (\begin{matrix} a_2 \\ b_2 \end{matrix} \right ) \text{ with } T_{ar} = \left (\begin{matrix} \tfrac{1}{t} & \tfrac{r^*}{t^*} \\ \tfrac{r}{t} & \tfrac{1}{t^*} \end{matrix} \right )\label{eq3.7.17} \]

де ми припустили, що багатошарове AR-покриття без втрат. Тут\(r\) і\(t\) є комплексні коефіцієнти для відображення та передачі на порту 1, припускаючи вільне закінчення відбиття порту 2. Back-mirror MB, як передбачається ідеально підібраний до першого шару в AR-покритті, має повне відображення над загальною смугою пропускання, що розглядається. Таким чином, його складна відбивна здатність в діапазоні інтересів задається

\[\rho_b = e^{j \phi_b (\omega)}\label{eq3.7.18} \]

Фаза\(\phi_b (\omega)\) визначається шуканою груповою затримкою дисперсії

\[GDD_b = -d^2 \phi_b (\omega) /d\omega^2 \nonumber \]

до невизначеної постійної фази і групової затримки на центральній частоті дзеркала,\(\omega_c\). Всі похідні фази вищого порядку визначаються потрібною дисперсією дзеркала. Аналітичні формули для проектування DCM, що показують спеціально розроблені дисперсійні властивості без урахування задачі відповідності з навколишнім повітрям, можна знайти в [73]. Отримана загальна дзеркальна відбивна здатність, включаючи AR-покриття, випливає з (\(\ref{eq3.7.17}\))

\[\rho_{tot} = \dfrac{t}{t^*} \rho_b \dfrac{1 - r^*/\rho_b}{1 - r \rho_b} \nonumber \]

Для окремого випадку ідеально відбиваючого заднього дзеркала згідно Equation (\(\ref{eq3.7.18}\)) отримаємо

\[\rho_{tot} = \dfrac{t}{t^*} e^{j\phi_b (\omega)} \dfrac{1 - z^*}{1-z}, \text{ with } z = re^{j\phi_b (\omega)} \nonumber \]

Нова відбивна здатність знову єдність, але нові внески у фазу отриманої відбивної здатності з'являються через недосконалі властивості передачі AR-покриття. З коефіцієнтом пропускання AR-покриття

\[t = |t| e^{j \phi_t}, \nonumber \]

Загальна фаза коефіцієнта відбиття стає

\[\phi_{tot} = 2\phi_t + \phi_b (\omega) + \phi_{GTI} \nonumber \]

із

\[\phi_{GTI} = 2 \arctan \left [ \dfrac{Im \{z\}}{1 + Re \{z\}}\right ] \nonumber \]

\(\phi_t\)Ось фаза коефіцієнта пропускання і\(\phi_{GTI}\) є фазою за рахунок інтерферометра Жира-Турнуа\(r \ne 0\), створеного неідеальним AR-покриттям, т. Е. Фаза\(\phi_t\) хорошого AR-покриття, тобто\(|r| < 0.1\) лінійна і, отже, не вносить небажаних коливань в ГД і ГДД. Однак фаза швидко\(\phi_{GTI}\) змінюється, оскільки\(\phi_b (\omega)\) змінюється\(2\pi\) протягом декількох в діапазоні частот, що цікавить через монотонну групову затримку заднього дзеркала. Розмір цих коливань масштабується з якістю AR-покриття, т\(|r|\). Е. Таким чином, коливання ГДД зменшуються при меншій залишковій відбивній здатності AR-покриття. Припускаючи, що відбивна здатність\(r\) реальна і менша або дорівнює 0,1, коливання в груповій затримці і групової затримки дисперсії легко оцінюються по

\[T_{g, GTI} = \dfrac{d\phi_{GTI}}{d\omega} \approx -r T_{gb} (\omega) \cos [\phi_b (\omega)] \nonumber \]

із

\[\begin{array} {rcl} {T_{gb} (\omega)} & = & {-d\phi_b (\omega)/d\omega,} \\ {GDD_{GTI}} & = & {\tfrac{d^2\phi_{GTI}}{d\omega^2}} \\ {} & \approx & {r(T_{gb}^2 (\omega) \sin [\phi_b (\oemga)] - GDD_b \cos [\phi_b (\omega)])} \end{array} \nonumber \]

GTI-відбиття складаються узгоджено, коли багаторазові відбиття на щебетаних дзеркалах відбуваються всередині лазера протягом одного туди-назад, що призводить до до і після імпульсів, якщо механізм блокування режиму недостатньо сильний, щоб придушити їх достатньо. Експериментальні результати показують, що залишкове відображення в AR-покритті\(r < 0.01\) і менших, в залежності від кількості відображень в зворотному напрямку, потрібно для того, щоб до- і пост-імпульси були досить придушені. Це відповідає AR-покриттю з меншою, ніж\(10^{-4}\) залишкова потужність відбивної здатності, яка може бути досягнута лише в дуже обмеженому діапазоні, як обговорювалося вище.

У обмеженому діапазоні довжин хвиль 350 нм зосереджено близько 800 нм низькі залишкові потужності відбивні здатності настільки малі, наскільки\(10^{-4}\) були досягнуті ефективно після повторної оптимізації секції AR-покриття та подвійної щебетаної секції, щоб сформувати комбіновану відповідну секцію вищої якості відповідності. Для ще більшої пропускної здатності, наближаючись до октави, залишкова потужність відбивної здатності вже\(10^{-4}\) неможлива [68]. Вихід з цього обмеження пропонує спостереження, що когерентне віднімання до- і пост-імпульсів до першого порядку в\(r\) можливо шляхом відображення на дзеркальній парі М1 і М2, див. Рис. 3.20 (а) і (б). Серія двох відображень на дзеркалі з відбивною здатністю (3.97) і на аналогічному дзеркалі з додатковим фазовим зсувом\(\pi\) між AR-покриттям і заднім дзеркалом, що має відбивну здатність (3.97) де\(z\) замінено на\(-z\), призводить до когерентного віднімання GTI- першого порядку ефекти. Отримана сумарна відбивна здатність двох відображень задається добутком окремих комплексних відбивних здатностей, що припускають однакове AR-покриття

\[\rho_{tot,2} = -\left (\dfrac{t}{t^*} \right )^2 e^{i2\phi_b (\omega)} \dfrac{1 - z^*^2}{1 - z^2} \nonumber \]

Тепер шкала GTI-ефектів, як потужність відбивної здатності AR-покриття\(r^2\) замість амплітудної відбивної здатності\(r\), що є величезним поліпшенням, оскільки можна розробити AR-покриття до матеріалу низького індексу Si02 дзеркала з залишковою потужністю відбивної здатності між 0. 001 і 0,01 при цьому охоплюючи одну октаву смуги пропускання [68]. Однак не існує жодного фізичного шару, який генерує фазовий зсув\(\pi/2\) протягом одного проходу для всіх частотних компонентів, що містяться в октаві. Тим не менш, шар з товщиною чверті хвилі на центральній частоті є хорошим стартовим дизайном. Тоді заднє дзеркало MB у дзеркалі М2 можна переоптимізувати, щоб подбати про відхилення від товщини хвилі на чверть далі від центральної частоти, оскільки заднє дзеркало діє як високодисперсійне середовище, де затримка фази або групи можуть бути розроблені за бажанням.

Малюнок 3.22: Відбивна здатність дзеркала з вікном насоса показана у вигляді товстої суцільної лінії зі шкалою зліва. Мета проектування групової затримки для ідеальної компенсації дисперсії безпризмного лазера Ti:Sapphire показана у вигляді товстої штрих-пунктирної лінії зі шкалою праворуч. Індивідуальна групова затримка спроектованих дзеркал показана у вигляді тонкої лінії, а її середня - пунктирною лінією, яка практично ідентична проектній меті в діапазоні довжин хвиль форми 650-1200 нм. Виміряна групова затримка за допомогою інтерферометрії білого світла показана як товста суцільна лінія від 600-1100 нм. Поза 1100 нм чутливість використовуваного Si- детектора запобігала подальшим вимірюванням.. Малюнок MIT OCW.

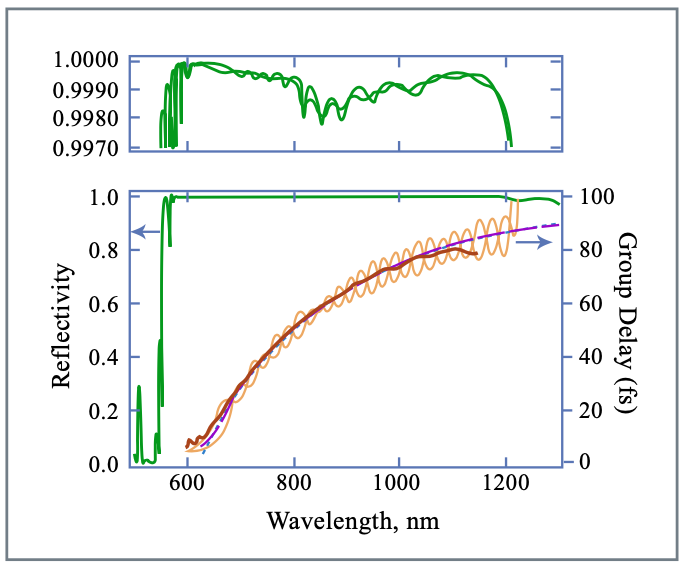
На малюнку 3.23 показана на верхньому графіку проектована відбивна здатність обох дзеркал пари у високій роздільній здатності з урахуванням поглинання в шарах. На графіку нижче показана відбивна здатність дзеркала, яке має крім того високу пропускну здатність між 510-550 нм для накачування кристала Ti: Sapphire. Кожне дзеркало складається з 40 пар шарів\(\ce{SiO2}\) і\(\ce{TiO2}\) виготовлено з використанням іонно-променевого напилення [74, 75]. Обидві дзеркальні відбивні здатності охоплюють більше однієї октави смуги пропускання від 580 нм до 1200 нм або 250 до 517 ТГц, із середньою відбивною здатністю близько 99,9%, включаючи поглинання в шарах. Крім того, дзеркальна дисперсія коригує дисперсію другого та вищого порядку всіх внутрішньопорожнинних елементів, таких як кристал Ti: сапфір та тонкі, малі кутові\(\ce{BaF2}\) клини, для точного регулювання дисперсії від 650 нм до 1200 нм у межах 12 відскоків, що відбуваються в одному зворотному напрямку. Вибір для нижньої межі довжини хвилі в компенсації дисперсії визначається і обмежується вікном насоса Ti:Sapphire. Вимірювання дисперсії проводилося за допомогою інтерферометрії білого світла [77], приблизно до 1100 нм через згортання кремнієвого детектора. Коливання в груповій затримці кожного дзеркала приблизно в 10 разів більше, ніж у високоякісних DCM, що охоплюють смугу пропускання 350 нм [?]. Однак в середній груповій затримці обох дзеркал коливання ідеально пригнічуються через скасування більш ніж в десять разів. Тому ефективна залишкова відбивна здатність дзеркальної пари, що охоплює одну октаву\(r^2\), навіть менша, ніж у звичайних DCM.

Методи компенсації активної дисперсії

Розроблено різні схеми активного компресії імпульсів на основі використання рідкокристалічних модуляторів (ЛКМ), акустооптичних модуляторів (АОМ), механічно деформованих дзеркал.

Компенсація дисперсії за допомогою рідкокристалічних моду

Малюнок 3.23: Пара решітки та формувач імпульсів LCM відповідно до Вайнера та спадщини [88]. Для формування амплітуди та фази необхідні два формувачі імпульсів з амплітудою та фазовою маскою. Малюнок MIT OCW.

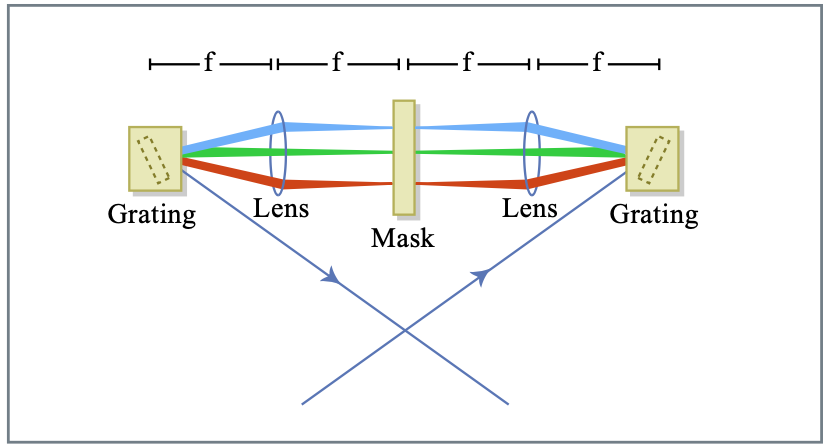
Методика формування імпульсів [84], заснована на використанні LCM для стиснення імпульсів, пропонує перевагу великої пропускної здатності (300-1500 нм) та адаптивного фазового управління in situ, див. Рисунок 3.23. У 1997 р. Єлін\(et\ al\). [85] продемонстрував адаптивний метод компресії фемтосекундного імпульсу на основі LCM. Сильно щебетання 80-fs імпульси, що генеруються генератором, були відправлені в\(f\) 4-імпульсний формувач, що складається з пари тонких голографічних решіток передачі. Програмований одновимірний LCM, розміщений у площині Фур'є формувача, використовувався як оновлюваний фільтр для імпульсних спектральних маніпуляцій. Отримано імпульси коротше 11 фс (обмежена тривалість перетворення: 9 фс) з використанням алгоритму оптимізації адаптивного стиснення на основі пошуку у двовимірному просторі коефіцієнтів дисперсії другого та третього порядку. У 2001 році Karasawa et al. [86] продемонстрували компресію імпульсів до 5 фс широкосмугових імпульсів із заповненого аргоном порожнистого волокна, використовуючи лише LCM для фазової компенсації. Зовсім недавно [51] імпульси коротких до 3,8 фс були досягнуті за допомогою замкнутої комбінації рідкокристалічного просторового модулятора світла для адаптивного стиснення імпульсів та спектрально-фазової інтерферометрії для прямої реконструкції електричного поля (SPIDER) [87] вимірювань як сигнал зворотного зв'язку.

Однією з задач методу є пікселізація в площині Фур'є завдяки технології рідкокристалічної активної матриці. Дифракція на краях пікселів і поглинання чорною матрицею вводять паразитарні ефекти. Вимога про те, що фактична спектральна модуляція повинна наближатися до гладкої функції, незважаючи на фіксований, кінцевий розмір окремих елементів модулятора, обмежує часовий діапазон, за яким може бути досягнуто стиснення імпульсів [88]. Інші проблеми пов'язані з оптичним пошкодженням ЛКМ, що обмежує максимальну енергію імпульсу, і з високими втратами, що вносяться пристроєм.

Були запропоновані різні непікселізовані пристрої: Доррер\(et\ al\). повідомили про оптично адресований LCM (рідкокристалічний світловий клапан) [89]. Світловий клапан складається з двох безперервних прозорих електродів і суцільних шарів нематичного скрученого рідкого кристала і фотопровідного\(\ce{Bi12SiO20}\) (BSO). Локальна варіація освітленості шару BSO (в синьо-зеленій області спектра) викликає зміну провідності. Коли напруга подається між двома електродами, зміна провідності BSO призводить до зміни падіння напруги на рідкокристалічному шарі. Оскільки подвійне заломлення рідкого кристала залежить від напруги, створюється локальна варіація показника заломлення, що перетворюється на зміну оптичної фази локальної спектральної складової. Регулювання світлового клапана здійснюється за допомогою дисплейного пристрою. Ефекти пікселізації уникаються, оскільки сам світловий клапан є безперервним пристроєм. Управління світловим клапаном складніше, ніж для електрично адресованого ЛКМ. Більш того, через свою обмежену просторову частотну характеристику спектральна роздільна здатність обмежена.

Компенсація дисперсії за допомогою акустооптичних модуляторів

У 1997 році Турнуа запропонував акустооптичний програмований дисперсійний фільтр (AOPDF), для забезпечення великих діапазонно-компенсаційних діапазонів дисперсії [91]. Пристрій заснований на колінеарному акустооптичному взаємодії в дволучепреломляючому одновісному кристалі, див. Рис. Акустична частота є змінною функцією часу і забезпечує контроль над груповою затримкою дифракційного оптичного імпульсу. При цьому спектральна амплітуда дифрагованого імпульсу приводиться в дію інтенсивністю акустичного сигналу. Як показано в Ref. [91],\(E_{out}(t)\) оптичний вихід AOPDF пропорційний згортці оптичного входу\(E_{in}(t)\), а масштабований акустичний сигнал:

\[E_{out} (t) \propto E_{in} (t) otimes S(t/\alpha) \nonumber \]

де\(\alpha = \Delta n(V/c)\) коефіцієнт масштабування - відношення швидкості звуку до швидкості світла, що разів перевищує різницю індексів між звичайною і надзвичайною хвилями. Тому, генеруючи належну функцію\(S(t)\), можна генерувати будь-яку довільну згортку з тимчасовою роздільною здатністю, заданою оберненою пропускною здатністю фільтра. Такі пристрої були використані в кілогерцових лазерних ланцюгах з підсиленням чирпових імпульсів, що компенсують звуження посилення і залишкові фазові похибки за допомогою AOPDF, що призвело до генерації 17-fs імпульсів з обмеженою трансформацією [92]. Загальна пропускна здатність становить 10- 50%, в залежності від пропускної здатності пристрою. Можливі пристрої, що наближаються до однієї октави по пропускній здатності.

Малюнок 3.24: Акустооптичний програмований формувач імпульсів. Один елемент може формувати амплітуду і фазу імпульсу.

Компенсація дисперсії за допомогою деформованих дзеркал

Механічно деформовані дзеркала можуть бути використані для керування активною дисперсією, як запропоновано Heritage\(et\ al\) [93]. Зовсім недавно імпульсне стиснення було досягнуто за допомогою електростатично деформується, покритого золотом, мембранного дзеркала з нітриду кремнію, поміщеного в площині Фур'є носилки з\(4f\) нульовою дисперсією [94]. Мембрана була підвішена над масивом з 39 електродів приводу. Потенціал, застосований до кожного виконавчого механізму, генерує електростатичне тяжіння між мембраною та електродом, викликаючи тим самим деформацію дзеркальної поверхні, що перетворюється на модуляцію фази спектральних компонентів вхідного імпульсу. Загальна різниця фаз -\(\Delta z\) це\(\phi = 2(2\pi)\Delta z/\lambda\), де прогин дзеркала. Мінімальний радіус кривизни дзеркальної мембрани задається\(R = T/P\) тим, де\(T\) знаходиться натяг мембрани і\(P\) є максимальним електростатичним тиском. Це обмеження кривизни мембрани обмежує можливість дзеркальної корекції фаз вищого порядку. Основними перевагами цього методу є наступні: фазова модуляція плавно змінюється; зменшені втрати за рахунок високої відбивної здатності (97%) дзеркала; відносно висока щільність приводу. Експерименти були проведені з замкненим режимом Ti:Sapphire лазером, де деформоване дзеркало рестиснуло імпульс 15 fs, попередньо розтягнутий до 90 фс дисперсією в склі, назад приблизно до межі смуги пропускання [94].

Нещодавно контроль дисперсії над смугою пропускання ~ 220 ТГц був продемонстрований А.Baltuska et al. [95] за допомогою компресора, що складається з пари щебетаних дзеркал і лінії розсіювання решітки з гнучким дзеркалом, керованим комп'ютером, розташованим у фокальній площині. Загальна пропускна здатність формувача імпульсів становила менше 12% через низьку дифракційну ефективність решітки. Використовуючи цей компресор, видимі ближні ІК імпульси, що генеруються оптичним параметричним посиленням, були стиснуті до тривалості 4-fs.

Техніка стиснення порожнистих волокон

Одномодове волокно дозволяє стискати лише імпульси низької енергії. У 1996 році група DeSilvestri в Мілані [48] розробила методику, яка дозволяє генерувати кілька циклів світлових імпульсів з енергіями в міліджоулевому діапазоні. Методика заснована на поширенні лазерних імпульсів в порожнистому волокні, заповненому благородними газами (техніка стиснення порожнистих волокон), див. Рис. 3.25. Режими порожнистого волокна є дірявими режимами, тобто вони відчувають втрати випромінювання. Однак є один режим,\(_{11}\) режим EH, який має значно менші втрати, ніж режими вищого порядку. Цей режим використовується для компресії імпульсів. Нелінійний індекс у волокні можна контролювати за допомогою тиску газу. Типові діаметри волокон 100-500 мкм, а типовий тиск газу знаходиться в діапазоні 0,1-3bar. Як і у випадку зі стисненням волокон, важливо враховувати оптимізацію нелінійної взаємодії та дисперсії. Необхідно враховувати як середню, так і хвилеводну дисперсію. Детальніше див. [107].

Малюнок 3.25: Техніка стиснення порожнистих волокон [48]

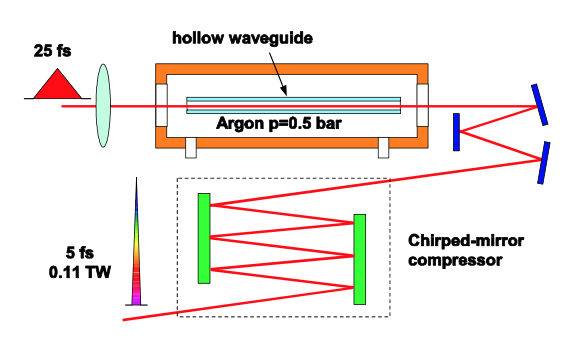
На даний момент техніка стиснення порожнистих волокон є єдиним способом генерувати суб-10fs міліджоульних імпульсів. Це зміниться незабаром з появою параметричного щебетання імпульсного посилення.