Skip to main content
LibreTexts - Ukrayinska

2.7: Відносини Крамерса-Кроеніга

  1. Last updated
  2. Save as PDF
  • Page ID
    32090

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Лінійна сприйнятливість - це частотна характеристика лінійної системи до прикладного електричного поля, яка є причинним, а тому реальна і уявна частини підкоряються відносинам Крамерса-Кроеніга

    \[\chi_r (\Omega) = \dfrac{2}{\pi} \int_{0}^{\infty} \dfrac{\omega \chi_i (\omega)}{\omega^2 - \Omega^2} d\omega = n^2 (\Omega) - 1, \nonumber \]

    \[\chi_i (\Omega) = -\dfrac{2}{\pi} \int_{0}^{\infty} \dfrac{\Omega \chi_r (\omega)}{\omega^2 - \Omega^2} d\omega. \nonumber \]

    У прозорих середовищах працює далеко від резонансів. Тоді поглинання або уявна частина сприйнятливості може бути наближена

    \[\chi_i (\Omega) = \sum_i A_i \delta (\omega -\omega_i) \nonumber \]

    та результати співвідношення Крамерса-Кроеніга в рівнянні Сельмайєра для показника заломлення

    \[\begin{align*} n^2 (\Omega) &= 1 + \sum_i A_i \dfrac{\omega_i}{\omega_i^2 - \Omega^2} \\[4pt] &= 1 + \sum_i a_i \dfrac{\lambda}{\lambda^2 - \lambda_i^2} \end{align*} \nonumber \]

    Для прикладу в таблиці 2.1 наведені коефіцієнти Селлмейєра для плавленого кварцу і сапфіру.

      Плавлений кварц Сапфір
    \(a_1\) 0.6961663 1.023798
    \(a_2\) 0.4079426 1.058364
    \(a_3\) 0,8974794 5.280792
    \(\lambda_1^2\) \(4.679148 \cdot 10^{-3}\) \(3.77588 \cdot 10^{-3}\)
    \(\lambda_2^2\) \(1.3512063 \cdot 10^{-2}\) \(1.22544 \cdot 10^{-2}\)
    \(\lambda_3^2\) \(0.9793400 \cdot 10^{2}\) \(3.213616 \cdot 10^{2}\)
    Таблиця 2.1: Таблиця з коефіцієнтами Сельмейєра для плавленого кварцу і сапфіру.

    Типова ситуація для матеріалу, що має резонанси в УФ і ІЧ, наприклад скла, показана на малюнку 2.12

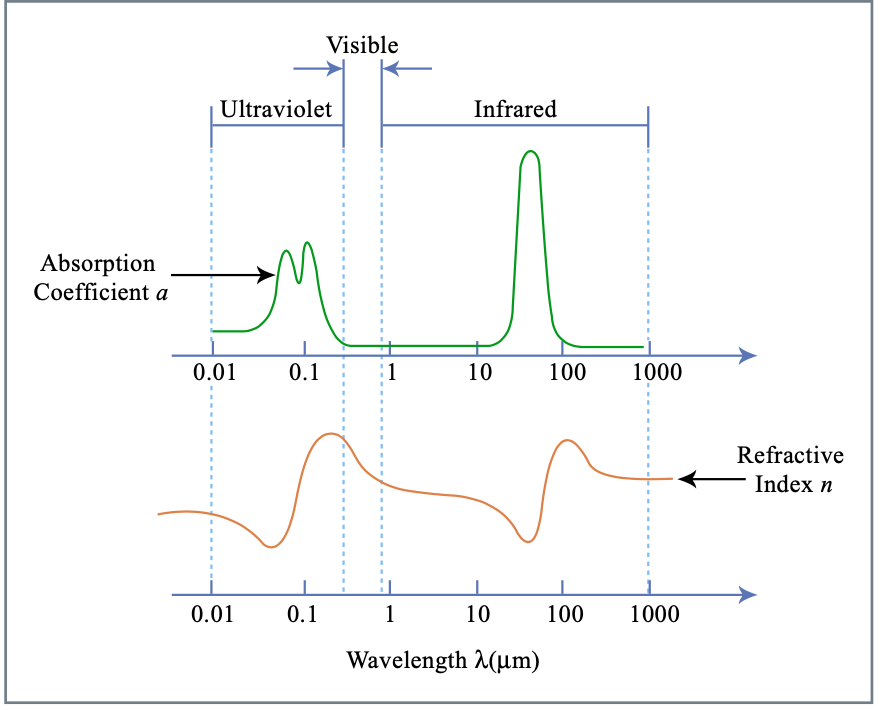
    2021-04-06 пн
    Малюнок 2.12: Типовий розподіл ліній поглинання в середовищі, прозорому у видимому. Малюнок MIT OCW.

    Регіони, де показник заломлення зменшується з довжиною хвилі, зазвичай називають нормальним діапазоном дисперсії, а протилежною поведінкою - аномальною дисперсією.

    \[\begin{array} {rcl} {\dfrac{dn}{d\lambda}} & < & {\text{0: normal dispersion (blue refracts more than red)}} \\ {\dfrac{dn}{d\lambda}} & > & {\text{0: abnormal dispersion}} \end{array}\nonumber \]

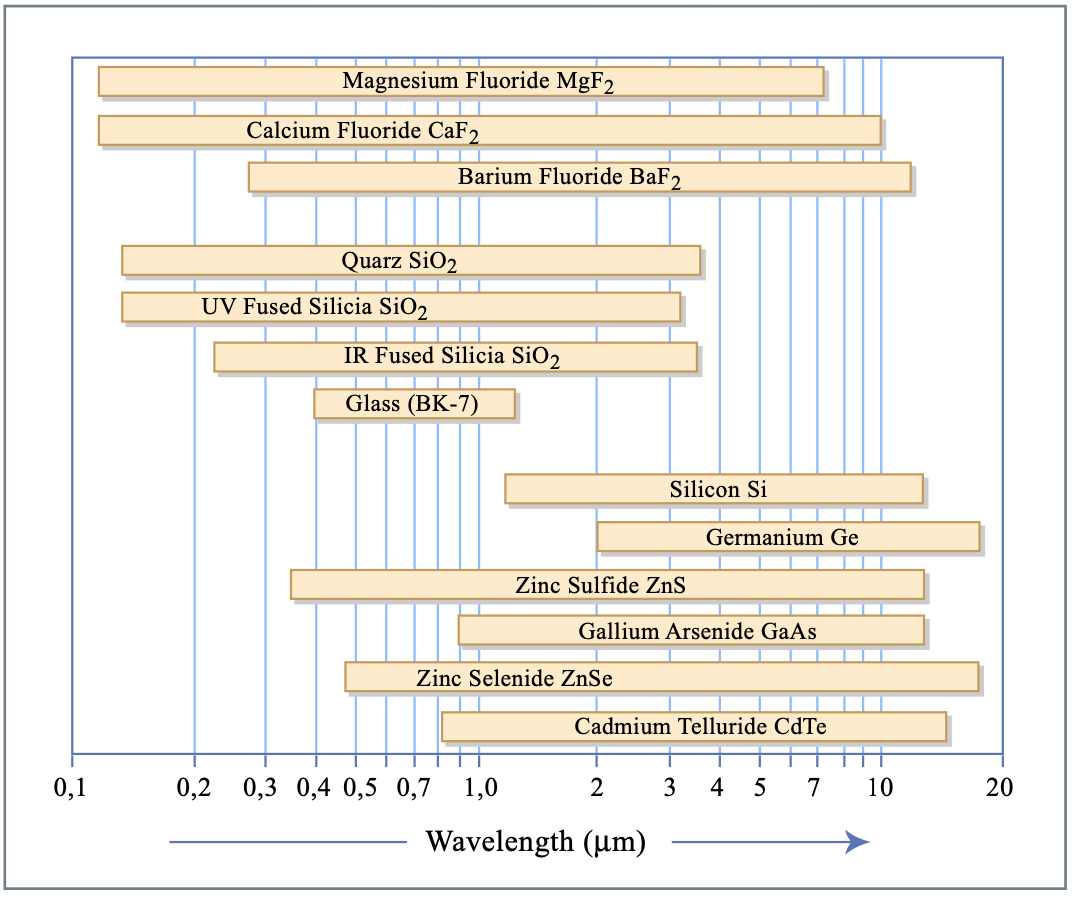
    На рис.2.13 показаний діапазон прозорості деяких часто використовуваних носіїв.

    2021-04-06 пнг
    Малюнок 2.13: Діапазон прозорості деяких матеріалів. Малюнок MIT OCW.