1.4: Огляд лазерних основ

Лінійні та кільцеві порожнини:

Малюнок 1.9: Можливі конфігурації порожнини. (а) Схема лінійного резонаторного лазера. (б) Схема кільцевого лазера [1]

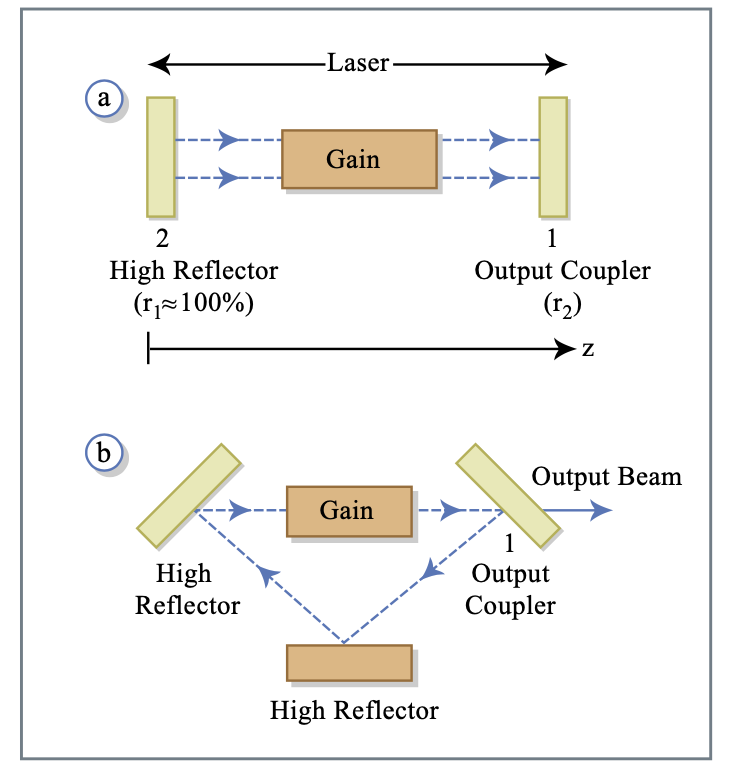
Стаціонована робота: Електричне поле повинно повторюватися після однієї поїздки в обидва кінці. Розглянемо монохроматичне лінійно поляризоване поле

$$E(z, t) = \Re\{ E_0 e^{j(\omega t - kz)}\}, \nonumber$$

де

$$k = \dfrac{\omega}{c} n \nonumber$$

постійна поширення в середовищі з показником заломлення$n$.

Розглянемо лінійний резонатор на малюнку 1.9а. Поширення від (1) до (2) визначається$n = n' + jn''$ (комплексний показник заломлення), при цьому електричне поле задається

$$E = \Re \{ E_0 e^{\tfrac{\omega}{c} n_g'' \ell_g} e^{j\omega t} e^{-j \tfrac{\omega}{c}(n_g' \ell_g + \ell_a)} \}, \nonumber$$

де$n_g$ - складний показник заломлення середовища посилення (за межами середовища посилення$n = 1$$\ell_g$ приймається), - довжина середовища посилення,$\ell_a$ є зовнішнім середовищем посилення і$\ell = n_g \ell_g + \ell_a$ довжина оптичного шляху в резонаторі.

Поширення назад до (1), тобто одна повна поїздка в обидва кінці призводить до

$$E = \Re \{ r_1 r_2 e^{2\tfrac{\omega}{c} n_g'' \ell_g} E_0 e^{j\omega t -j 2 \tfrac{\omega}{c} \ell} \} \Rightarrow r_1 r_2 e^{2 \tfrac{\omega}{c} n_g'' \ell_g} = 1, \nonumber$$

тобто посилення дорівнює втраті, а крім того, отримуємо умову фази

$$\dfrac{2\omega \ell}{c} = 2m\pi. \nonumber$$

Фазовий стан визначає резонансні частоти, т. Е.

$$\omega_m = \dfrac{m\pi c}{\ell} \nonumber$$

і

$$f_m = \dfrac{mc}{2\ell}. \nonumber$$

Відстань між режимами поздовжніх режимів становить

$$\Delta f = f_m - f_{m - 1} = \dfrac{c}{2\ell} \nonumber$$

(true тільки якщо немає дисперсії, тобто$n \ne n(\omega)$). Припустимо, незалежні від частоти втрати порожнини і посилення у формі дзвінка (див. Рис.

Малюнок 1.10: Спектри посилення лазера та втрат порожнини, розташування поздовжнього режиму та вихід лазера для роботи багатомодового лазера.

Малюнок 1.11: Спектри посилення та втрат, місця поздовжнього режиму та вихід лазера для роботи одномодового лазера.

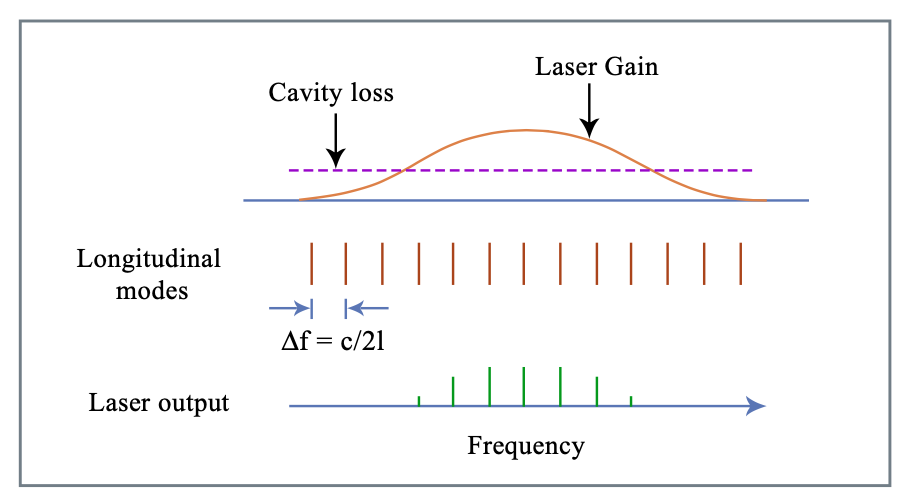
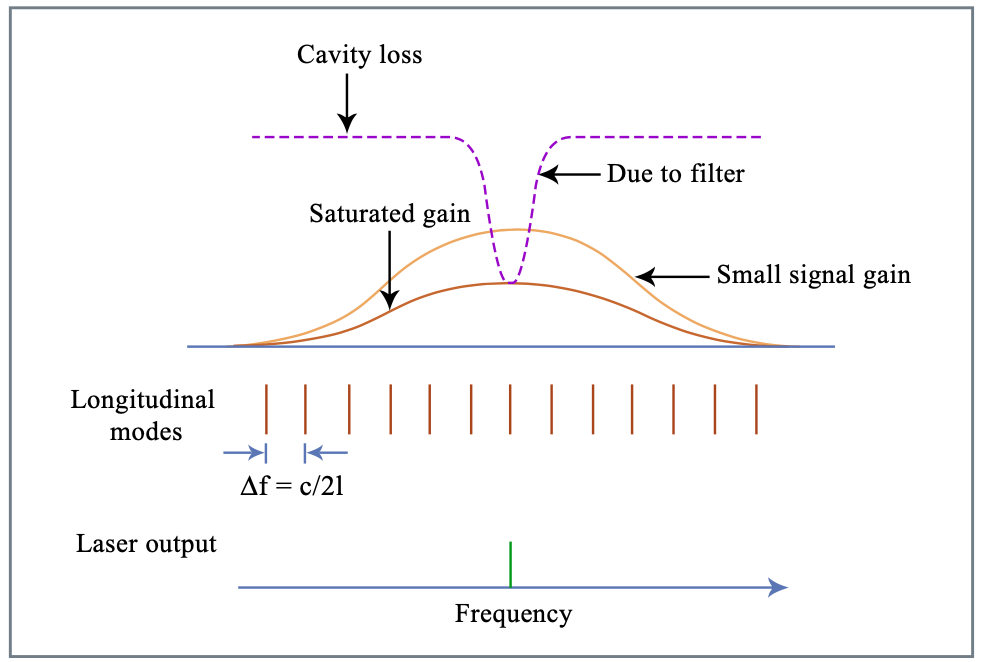
Для забезпечення роботи однієї частоти використовуйте фільтр (еталон); розрізняти be- tween однорідно і неоднорідно розширені середовища посилення, ефекти спектрального горіння отворів! Розрізняють невелике посилення сигналу g0 в обидва кінці, тобто посилення інтенсивності лазера$I \to 0$, і великий коефіцієнт посилення сигналу, найчастіше задається

$$g = \dfrac{g_0}{1 + \tfrac{I}{I_{sat}}}, \nonumber$$

де$I_{sat}$ - інтенсивність насичення. Посилення посилення відповідає за посилення сталого стану (див. Рис. 1.11), а однорідно розширене посилення передбачається.

Для генерації коротких імпульсів, тобто коротше, ніж час обертання порожнини, ми хочемо мати багато поздовжніх режимів, що працюють у сталому стані. Для багатомодового лазера лазерне поле задається

$$E(z, t) = \Re \left [ \sum_{m} \hat{E}_m e^{j(\omega_m t - k_m z + \phi_m)} \right ], \nonumber$$

$$\omega_m = \omega_0 + m \Delta \omega = \omega_0 + \dfrac{m\pi c}{\ell}, \nonumber$$

$$k_m = \dfrac{\omega_m}{c}, \nonumber$$

де символ$\hat{\ }$ позначає величину частотної області. Рівняння (1.4.10) можна переписати як

$$E(z,t) = \Re \left \{e^{j \omega_0 (t - z/c) \sum_m \hat{E}_m e^{j (m \Delta \omega (t - z/c) + \phi_m)} \right\} \nonumber$$

$$= \Re [A(t - z/c) e^{j\omega_0 (t - z/c)} ] \nonumber$$

зі складним конвертом

$$A(t - \dfrac{z}{c}) = \sum_m E_m e^{j (m \Delta \omega (t - z/c) + \phi_m)} = \text{complex envelope (slowly varying).} \nonumber$$

$e^{j\omega_0 (t - z/c)$є несучою хвилею (швидке коливання). І носій, і конверт рухаються з однаковою швидкістю (не передбачається розсіювання). Функція оболонки періодична з періодом

$$T = \dfrac{2\pi}{\Delta \omega} = \dfrac{2\ell}{c} = \dfrac{L}{c}. \nonumber$$

$L$довжина в обидва кінці (оптична)!

Приклад$\PageIndex{1}$

Приймаємо$N$ режими з рівними амплітудами$E_m = E_0$ і рівними фазами$\phi_m = 0$, і при цьому огинач задається

$$A (z, t) = E_0 \sum_{m = -(N-1)/2}^{(N - 1)/2} e^{j(m \Delta \omega (t - z/c))} \nonumber$$

З

$$\sum_{m = 0}^{q - 1} a^m = \dfrac{1 - a^q}{1 - a}, \nonumber$$

отримуємо

$$A(z, t) = E_0 \dfrac{\sin [\tfrac{N \Delta \omega}{2} ( t - \tfrac{z}{c})]}{\sin [\tfrac{\Delta \omega}{2} ( t - \tfrac{z}{c})]} \nonumber$$

Інтенсивність лазера$I$ пропорційна$E(z,t)^2$, усереднена за один оптичний цикл:$I \sim |A(z, t)|^2$. При$z = 0$, отримуємо

$$I(t) \sim |E_0|^2 \dfrac{\sin^2 (\tfrac{N \Delta \omega t}{2})}{\sin^2 (\tfrac{\Delta \omega t}{2})}. \nonumber$$

Малюнок 1.12: (а) режим блокування лазерного виходу з фазою постійного режиму. (б) Лазерний вихід з випадково фазованими режимами.

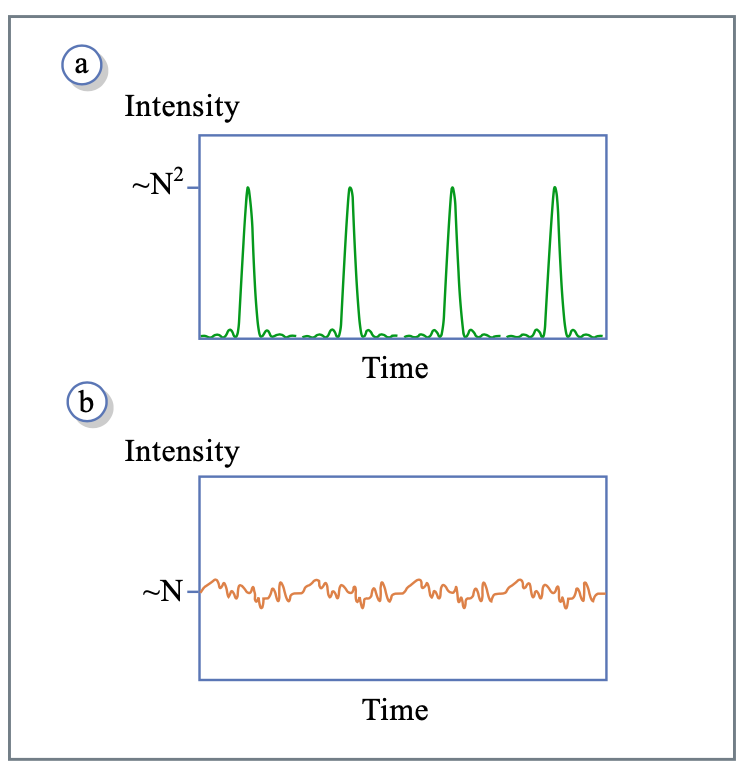
(a) Періодичні імпульси, задані рівнянням 1.4.19, період$T = 1/ \Delta f = L/c$

• тривалість імпульсу

$$\Delta t = \dfrac{2\pi}{N \Delta \omega} = \dfrac{1}{N\Delta f} \nonumber$$

• пікова інтенсивність ~$N^2 |E_0|^2$
• середня інтенсивність ~$N |E_0|^2 \Rightarrow$ пікова інтенсивність посилюється на коефіцієнт$N$.

(b) Якщо фази режимів не заблоковані, тобто$\phi_m$ випадкова послідовність

• Інтенсивність коливається випадковим чином щодо середнього значення ($\sim N |E_0|^2$), так само, як і modelocked case

• час кореляції становить$\Delta t_c \approx \dfrac{1}{N \cdot \Delta f}$

• Коливання все ще періодичні з періодом$T = 1/\Delta f$.

У звичайному багатомодовому лазері,$\phi_m$ змінюється більше$t$.