Skip to main content
LibreTexts - Ukrayinska

1.2: Імпульсні характеристики

  1. Last updated
  2. Save as PDF
  • Page ID
    32223

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Найчастіше спостерігається не ізольований пульс, а скоріше ланцюг імпульсів.

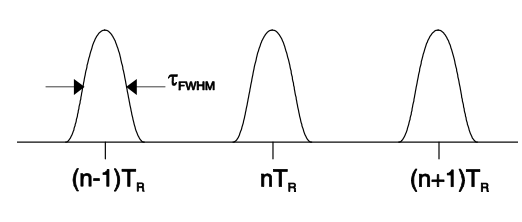
    2021-03-24 пнг
    Малюнок 1.1: Періодичний імпульсний ланцюг

    \(T_R\): час повторення імпульсу
    \(W\)
    \(P_{ave} = W/T_R\): енергія імпульсу: середня потужність
    \(\tau{\text{FWHM}}\) - повна ширина на половину максимуму оболонки інтенсивності імпульсу у часовій області.
    Пікова потужність задається

    \[P_p = \dfrac{W}{\tau{\text{FWHM}}} = P_{ave} \dfrac{T_R}{\tau{\text{FWHM}}} \nonumber \]

    і пікове електричне поле задається

    \[E_p = \sqrt{2 Z_{F_0} \dfrac{P_p}{A_{\text{eff}}} \nonumber \]

    \(A_{\text{eff}}\)є поперечним перерізом променя і\(Z_{F_0} = 377 \Omega\) є імпедансом вільного простору.

    Часові шкали:

    \[\begin{array} {lcl} {\text{1 ns}} & \sim & {30\text{ cm (high-speed electronics, GHz}} \\ {\text{1 ps}} & \sim & {300\ \mu\text{m}} \\ {\text{1 fs}} & \sim & {\text{300 nm}} \\ {1 \text{ as} = 10^{-18} s} & \sim & {\text{0.3 nm = 3} \mathring{A} \text{ (typ-lattice constant in metal)}} \end{array} \nonumber \]

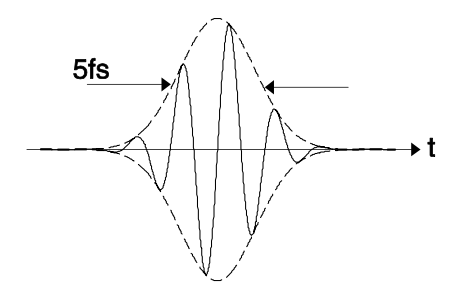
    Найкоротші імпульси, що генеруються на сьогоднішній день, становлять близько 4 - 5\((\lambda/c = 2.7\) фс при 800 нм фс), менше двох оптичних циклів і 250 як при 25 нм. Для малоциклових імпульсів важливе значення стає електричне поле, а не тільки інтенсивність!

    2021-03-24 пнг
    Малюнок 1.2: Форма хвилі електричного поля імпульсу 5 fs на центральній довжині хвилі 800 нм. Електричне поле залежить від фази несучої оболонки.

    середня потужність:

    \[\begin{array} {cl} {P_{ave} \sim} & {\text{1W, up to 100 W in progress.}} \\ {\ } & {\text{kW possible, not yet pulsed}} \end{array} \nonumber \]

    частоти повторення:

    \[T_R^{-1} = f_R = \text{m Hz - 100 GHz}\nonumber \]

    енергія імпульсу:

    \[W = 1pJ - 1kJ\nonumber \]

    ширина імпульсу:

    \[\tau_{\text{FWHM}} = \begin{array} {ll} {\text{5 fs - 50 ps,}} & {\text{modelocked}} \\ {\text{30 ps - 100 ns,}} & {\text{Q - switched}} \end{array}\nonumber \]

    пікова потужність:

    \[P_p = \dfrac{\text{1 kJ}}{\text{1 ps}} \sim \text{1 PW},\nonumber \]

    отриманий з Nd:Glass (LLNL - США, [1] [2] [3]).

    Для типового лабораторного імпульсу пікова потужність становить

    \[P_p = \dfrac{\text{10 nJ}}{\text{10 fs}} \sim \text{1 MW}\nonumber \]

    пікове поле типового лабораторного імпульсу:

    \[E_p = \sqrt{2 \times 377 \times \dfrac{10^6 \times 10^{12}}{\pi \times (1.5)^2}} \dfrac{\text{V}}{\text{m}} \approx 10^{10} \dfrac{\text{V}}{\text{m}} = \dfrac{10\text{V}}{\text{nm}}\nonumber \]