Skip to main content
LibreTexts - Ukrayinska

8.2: Кут приймання

  1. Last updated
  2. Save as PDF
  • Page ID
    30885

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    У цьому розділі ми розглянемо проблему впорскування світла в волоконно-оптичний кабель. Проблема проілюстрована на рис\(\PageIndex{1}\).

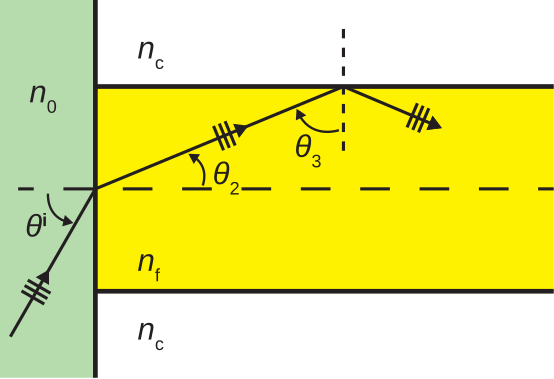
    m0192_fAA.png
    Малюнок\(\PageIndex{1}\): Ін'єкція світла в волоконно-оптичний кабель. (CC BY-SA 4.0; S. Lally)

    На цьому малюнку ми бачимо світло, що падає з середовища, що має показник заломлення\(n_0\), з кутом падіння\(\theta^i\). Світло передається з кутом пропускання\(\theta_2\) в волокно, а згодом падає на поверхню облицювання з кутом падіння\(\theta_3\). Щоб світло поширювалося без втрат всередині кабелю, потрібно, щоб

    \[\sin\theta_3 \ge \frac{n_c}{n_f} \label{m0192_eCAnm} \]

    оскільки цей критерій повинен бути дотриманий для того, щоб відбувалося повне внутрішнє відображення.

    Тепер розглянемо обмеження, яке накладає Equation\ ref {M0192_eCanm}\(\theta^i\). По-перше, відзначимо, що\(\theta_3\) пов'язано з\(\theta_2\) наступним:

    \[\theta_3 = \frac{\pi}{2} - \theta_2 \nonumber \]

    тому

    \ begin {вирівняти}\ sin\ theta_3 &=\ sin\ ліворуч (\ frac {\ pi} {2} -\ theta_2\ праворуч)\\ &=\ cos\ theta_2\ end {вирівняти}

    тому

    \[\cos\theta_2 \ge \frac{n_c}{n_f} \nonumber \]

    Квадратуючи обидві сторони, знаходимо:

    \[\cos^2\theta_2 \ge \frac{n_c^2}{n_f^2} \nonumber \]

    Тепер викликаємо тригонометричну ідентичність:

    \[1-\sin^2\theta_2 \ge \frac{n_c^2}{n_f^2} \nonumber \]

    Отже:

    \[\sin^2\theta_2 \le 1-\frac{n_c^2}{n_f^2} \label{m0192_e1} \]

    Тепер ми ставимося\(\theta_2\) до\(\theta^i\) використання закону Снелла:

    \[\sin\theta_2 = \frac{n_0}{n_f}\sin\theta^i \nonumber \]

    так може бути записано рівняння\ ref {m0192_e1}:

    \[\frac{n_0^2}{n_f^2}\sin^2\theta^i \le 1-\frac{n_c^2}{n_f^2} \nonumber \]

    Тепер вирішуючи для\(\sin\theta^i\), отримуємо:

    \[\sin\theta^i \le \frac{1}{n_0}\sqrt{ n_f^2 - n_c^2 } \nonumber \]

    Цей результат вказує на діапазон кутів падіння, які призводять до повного внутрішнього відбиття всередині волокна. Максимальне значення\(\theta^i\), яке задовольняє цій умові, відомо як кут приймання\(\theta_a\), так:

    \[\theta_a \triangleq \arcsin\left(\frac{1}{n_0}\sqrt{ n_f^2 - n_c^2 }\right) \nonumber \]

    Це призводить до наступного розуміння:

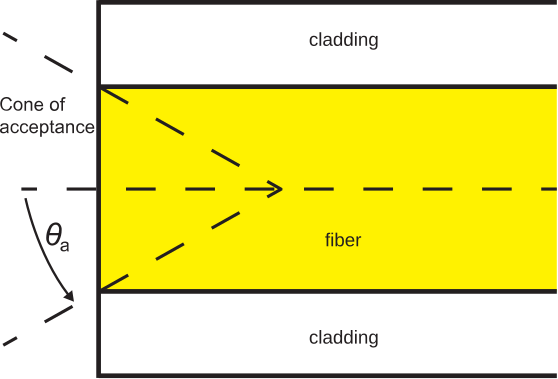
    Для того, щоб ефективно запустити світло у волокні, необхідно, щоб світло надходило зсередини конуса, що має півкут\(\theta_a\) по відношенню до осі волокна.

    Пов'язаний конус приймання проілюстрований на малюнку\(\PageIndex{2}\).

    m0192_fAcceptanceAngle.png
    Малюнок\(\PageIndex{2}\): Конус приймання. (CC BY-SA 4.0)

    Також прийнято визначати величину числової діафрагми NA наступним чином:

    \[\mbox{NA} \triangleq \frac{1}{n_0}\sqrt{ n_f^2 - n_c^2 } \label{m0192_eNA} \]

    Зверніть увагу,\(n_0\) що, як правило, дуже близький до\(1\) (відповідає захворюваності з повітря), тому прийнято бачити NA, що визначається як просто\(\sqrt{ n_f^2 - n_c^2 }\). Цей параметр зазвичай використовується замість кута прийняття в таблицях даних для волоконно-оптичного кабелю.

    Приклад\(\PageIndex{1}\): Acceptance angle

    Типові значення\(n_f\) і\(n_c\) для оптичного волокна - 1,52 і 1,49 відповідно. Які числові діафрагми і кут приймання?

    Рішення

    Використовуючи Equation\ ref {M0192_ENA} і припускаючи\(n_0=1\), ми знаходимо NA\(\cong \underline{0.30}\). Так як\(\sin\theta_a =\) Н.А., знаходимо\(\theta_a=\underline{17.5^{\circ}}\). Світло повинно надходити зсередини\(17.5^{\circ}\) від осі волокна, щоб забезпечити повне внутрішнє відображення всередині волокна.