6.9: Прямокутний хвилевід- Режими TE

Last updated
Save as PDF

Page ID: 30833

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Прямокутний хвилевід - це провідний циліндр прямокутного перерізу, який використовується для направлення поширення хвиль. Прямокутний хвилевід зазвичай використовується для транспортування радіочастотних сигналів на частотах в діапазоні СВЧ (3—30 ГГц) і вище. Поля в прямокутному хвилеводі складаються з ряду режимів поширення, що залежить від електричних розмірів хвилеводу. Ці режими широко класифікуються як поперечні магнітні (ТМ) або поперечні електричні (TE). У цьому розділі ми розглянемо режими TE.

\(\PageIndex{1}\)На малюнку показана цікава геометрія. Тут стіни розташовуються за адресою\(x=0\),,\(x=a\)\(y=0\), і\(y=b\); таким чином, розміри поперечного перерізу хвилеводу становлять\(a\) і\(b\). Передбачається, що внутрішня частина хвилеводу складається з матеріалу без втрат, що демонструє реальну проникність\(\mu\) та реальну діелектричну проникність\(\epsilon\), а стіни вважаються ідеально провідними.

Рисунок\(\PageIndex{1}\): Геометрія для аналізу полів у прямокутному хвилеводі.

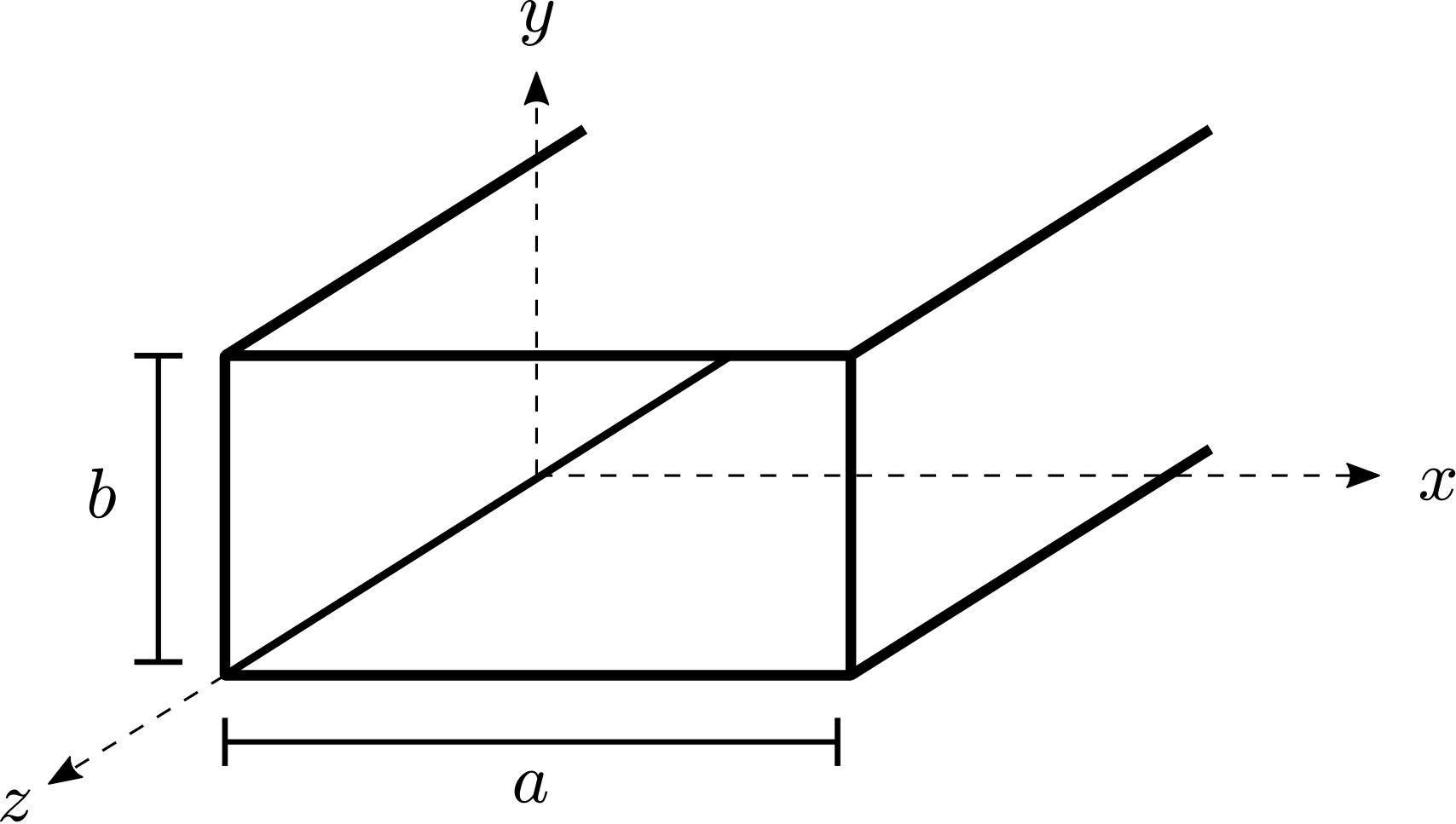
Обмежимо нашу увагу областю в межах хвилеводу, яка не містить джерел. Виражена в фазоровому вигляді, напруженість магнітного поля всередині хвилеводу регулюється хвильовим рівнянням:

\[\nabla^2 \widetilde{\bf H} + \beta^2 \widetilde{\bf H} = 0 \label{m0225_eWE} \]

де

\[\beta = \omega \sqrt{\mu \epsilon} \nonumber \]

Рівняння\ ref {M0225_EWE} є рівнянням з частинними похідними. Цього рівняння в поєднанні з граничними умовами, що накладаються ідеально провідними пластинами, достатньо для визначення унікального рішення. Це рішення найлегше визначити в декартових координатах, як ми зараз продемонструємо. Спочатку виражаємо\(\widetilde{\bf H}\) в декартових координатах:

\[\widetilde{\bf H} = \hat{\bf x}\widetilde{H}_x + \hat{\bf y}\widetilde{H}_y + \hat{\bf z}\widetilde{H}_z \label{m0225_eE} \]

Це полегшує розкладання Equation\ ref {M0225_EWE} на окремі рівняння\(\hat{\bf x}\), що регулюють\(\hat{\bf y}\), і\(\hat{\bf z}\) компоненти\(\widetilde{\bf H}\):

\ begin {вирівнювання}\ nabla^2\ широка ширина {H} _x +\ бета ^ 2\ ширина {H} _x &= 0\\\ nabla^2\ ширина {H} _y +\ бета^2\ ширина {H} _y &= 0\\\ nabla^2\ ширина {H} _z +\ beta^2\ широка ширина {H} _z &= 0\ end {вирівнювання}

Далі ми спостерігаємо, що оператор\(\nabla^2\) може бути виражений в декартових координатах наступним чином:

\[\nabla^2 = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2} \nonumber \]

тому рівняння, що регулюють декартові компоненти,\(\widetilde{\bf H}\) можуть бути записані наступним чином:

\ begin {вирівнювання}\ розрив {\ частковий ^ 2} {\ частковий x^2}\ widetilde {H} _x +\ розрив {\ частковий ^2} {\ частковий y^2}\ widetilde {H} _x +\ frac {\ частковий z ^ 2}\ widetilde {H} _x +\ beta^2\ widetilde де {H} _x &= 0\ мітка {M0225_EEFX}\\ розрив {\ часткова ^ 2} {\ часткова x^2}\ ширина {H} _y +\ розрив {\ частковий ^ 2} {\ частковий y^2}\ широкий {H} _y + \ frac {\ частковий ^ 2} {\ частковий z^2}\ широкий {H} _y +\ бета^2\ widetilde {H} _y &= 0\ мітка {M0225_EEFY}\\ розрив {\ часткова ^ 2} {\ часткова x^2}\ ширина {H} _z +\ frac {\ часткова ^ 2} {\ частковий y^2}\ широкий {H} _z +\ розрив {\ частковий ^ 2} {\ частковий z^2}\ широкий {H} _z +\ бета^2\ widetilde {H} _z &= 0\ мітка {m0225_EEFZ}\ кінець {вирівнювання}

Загалом, ми очікуємо, що загальне поле в хвилеводі буде складатися з односпрямованих хвиль, що поширюються в\(-\hat{\bf z}\) напрямках\(+\hat{\bf z}\) і. Ми можемо проаналізувати будь-яку з цих хвиль; тоді інша хвиля легко виводиться за допомогою симетрії, а загальне поле - це просто лінійна комбінація (суперпозиція) цих хвиль. Маючи це на увазі, ми обмежуємо свою увагу хвилею, що поширюється в\(+\hat{\bf z}\) напрямку.

У розділі 6.7 показано, що всі складові електричного та магнітного полів можна легко розрахувати один раз\(\widetilde{E}_z\) і\(\widetilde{H}_z\) відомі. Задача ще більше спрощується шляхом розкладання односпрямованої хвилі на компоненти ТМ і TE. При цьому розкладанні компонент TE визначається властивістю that\(\widetilde{E}_z=0\); тобто є поперечним (перпендикулярним) напрямку поширення. Таким чином, компонент TE повністю визначається по\(\widetilde{H}_z\). Рівняння 6.7.21 - 6.7.24 спростити стати:

\ begin {вирівнювання}\ widetilde {E} _x &= -j\ frac {\ омега\ му} {k_ {\ rho} ^2}\ розрив {\ часткова\ широка {H} _z} {\ часткова y}\ мітка {m0225_EEXU}\\ widetilde {E} _y &= +j\ frac {\ омега\ му} {k_ {\ rho} ^2}\ розрив {\ часткова\ широка {H} _z} {\ часткова х}\ мітка {m0225_EEYU}\\ ширина {H} _x &= -j\ frac {k_z} {k_ {\ rho} ^2}\ frac {\ часткова\ широка {H} _z} {\ часткова x}\ мітка {m0225_EHXU}\\ широка ширина {H} _y &= -j\ розрив {k_z} {k_ {\ rho} ^2}\ frac {\ часткова\ широка {H} _z} {\ часткова y}\ мітка {M0225_EHU}\ кінець {вирівняти}

де

\[k_{\rho}^2 \triangleq \beta^2 - k_z^2 \label{m0225_ekrho} \]

і\(k_z\) є постійною поширення фази; тобто хвиля, як передбачається, поширюється відповідно до\(e^{-jk_z z}\).

Тепер займемося проблемою знаходження\(\widetilde{H}_z\), яка потім повністю визначить поле ТЕ. Як і в розділі 6.7, ми визнаємо, що\(\widetilde{H}_z\) може бути представлений як коефіцієнт поширення\(e^{-jk_z z}\) разів на фактор, який описує варіації щодо решти просторових розмірів\(x\) і\(y\):

\[\widetilde{H}_z = \widetilde{h}_z(x,y) e^{-jk_z z} \nonumber \]

Підстановка цього виразу на Equation\ ref {M0225_EEFZ} і розділення загального коефіцієнта\(e^{-jk_z z}\) прибутковості:

\[\frac{\partial^2}{\partial x^2}\widetilde{h}_z + \frac{\partial^2}{\partial y^2}\widetilde{h}_z - k_z^2 \widetilde{h}_z + \beta^2 \widetilde{h}_z = 0 \nonumber \]

Останні два члени можуть бути об'єднані за допомогою Equation\ ref {m0225_ekrho}, що дає:

\[\frac{\partial^2}{\partial x^2}\widetilde{h}_z + \frac{\partial^2}{\partial y^2}\widetilde{h}_z + k_{\rho}^2 \widetilde{h}_z = 0 \label{m0225_eDE1} \]

Це рівняння з частинними\(\widetilde{h}_z\) похідними для в змінних\(x\) і\(y\). Це рівняння може бути вирішено за допомогою методики поділу змінних. У цій техніці ми визнаємо, що\(\widetilde{h}_z(x,y)\) можна записати як добуток функції,\(X(x)\) яка залежить тільки від\(x\), і функція,\(Y(y)\) яка залежить тільки від\(y\). Тобто,

\[\widetilde{h}_z(x,y) = X(x) Y(y) \nonumber \]

Підставивши цей вираз в Equation\ ref {M0225_edE1}, отримаємо:

\[Y\frac{\partial^2}{\partial x^2}X + X\frac{\partial^2}{\partial y^2}Y + k_{\rho}^2 XY = 0 \label{m0225_eDE2} \]

Далі діливши через на\(XY\), отримуємо:

\[\frac{1}{X}\frac{\partial^2}{\partial x^2}X + \frac{1}{Y}\frac{\partial^2}{\partial y^2}Y + k_{\rho}^2 = 0 \label{m0225_eDE3} \]

Зверніть увагу, що перший термін залежить тільки від\(x\), другий термін залежить тільки від\(y\), а решта термін є постійним. Тому сума першого і другого членів є постійною; а саме\(-k_{\rho}^2\). Оскільки ці терміни залежать від того\(x\) чи іншого\(y\), а не від обох, перший член повинен дорівнювати деякій константі, другий член повинен дорівнювати деякій константі, і ці константи повинні сумувати до\(-k_{\rho}^2\). Тому ми виправдовуємося в поділі рівняння на два рівняння наступним чином:

\ begin {вирівнювання}\ розрив {1} {X}\ розрив {\ частковий ^ 2} {\ частковий x^2} X + k_x^2 &= 0\ мітка {M0225_edE4x}\\ frac {1} {Y}\ розрив {\ частковий ^ 2} {\ частковий y^2} Y + k_y^2 &= 0\ мітка {0225_ede4y}\ кінець {вирівнювання}

де нові константи\(k_x^2\) і\(k_y^2\) повинні задовольняти

\[k_x^2+k_y^2 = k_{\rho}^2 \nonumber \]

Тепер множимо рівняння\ ref {M0225_edE4x} і\ ref {m0225_ede4y} на\(X\) і\(Y\), відповідно, знаходимо:

\ begin {вирівнювання}\ розрив {\ частковий ^ 2} {\ частковий x^2} X + k_x^2 X &= 0\ мітка {m0225_edE5x}\\ розрив {\ частковий ^2} {\ частковий y^2} Y + k_y^2 Y &= 0\ мітка {m0225_edE5Y}\ кінець {вирівнювання}

Це знайомі одновимірні диференціальні рівняння. Рішення такі: ¹

\ begin {вирівняти} X &= A\ cos\ ліворуч (k_x x\ праворуч) + B\ sin\ ліворуч (k_x x\ праворуч)\ мітка {M0225_ex}\ Y &= C\ cos\ ліворуч (k_y y\ праворуч) + D\ sin\ ліворуч (k_y y\ праворуч)\ мітка {M0225_EY}\ кінець {вирівнювання}

де\(A\),\(B\)\(C\), і\(D\) — як\(k_x\) і\(k_y\) — константи, які потрібно визначити. У цей момент ми спостерігаємо, що хвиля, яку ми шукаємо, може бути виражена наступним чином:

\ begin {вирівнювання}\ ширина {H} _z &=\ ширина {h} _z (x, y) e^ {-jk_z z}\ номер\ &= X (x) ~Y (y) ~e^ {-jk_z z}\ мітка {m0225_eezxYZ}\ кінець {вирівнювання}

Рішення по суті є завершеним за винятком значень констант\(A\)\(B\),\(C\),\(D\),\(k_x\), і\(k_y\). Значення цих констант визначаються шляхом застосування відповідної електромагнітної граничної умови. При цьому потрібно, щоб будь-яка складова,\(\widetilde{\bf E}\) яка є дотичною до ідеально провідної стіни, повинна дорівнювати нулю. Тому:

\ почати {вирівняти}\ ширина {E} _y\ ліворуч (x = 0\ праворуч) &= 0\\\ widetilde {E} _y\ ліворуч (x = а\ праворуч) &= 0\\\ widetilde {E} _x\ ліворуч (y = 0\\ праворуч) &= 0\\\ widetilde {E} _x\ ліворуч (y = 0\\ праворуч) &= 0\ end {вирівняти}

Посилаючись на рівняння\ ref {M0225_EEZxyz} і використовуючи рівняння\ ref {M0225_Eexu} -\ ref {M0225_EHYU}, отримаємо:

\ begin {вирівнювання}\ розрив {\ частковий} {\ частковий x} X\ лівий (x = 0\\ праворуч) &= 0\\\ гідророзриву {\ частковий} {\ частковий x} X\ лівий (x = a\ праворуч) &= 0\\\ frac {\ частковий} {\ частковий y} Y\ лівий (y=0\ праворуч) &= 0\\\ frac {\ partial}\ частковий y} Y\ лівий (y=b\ праворуч) &= 0\ end {вирівнювання}

Оцінюючи часткові похідні і розділивши загальні фактори\(k_x\) і\(k_y\), знайдемо:

\ почати {вирівняти} -A\ sin (k_x\ cdot 0) + Б\ cos (k_x\ cdot 0) &= 0\\ -A\ sin (k_x\ cdot a) + Б\ cos (k_x\ cdot a) &= 0\\ -C\ sin (k_y\ cdot 0) + D\ cos (k_y\ cdot 0) &= 0\\ -C\ sin (k_y\ cdot b) + D\ cos (k_y\ cdot b) &= 0\ кінець {вирівнювання}

Оцінка:

\ begin {вирівнювання} -A\ cdot 0 + B\ cdot 1 &= 0\ мітка {m0225_exbc1}\\ -A\ sin\ ліворуч (k_x а\ вправо) + B\ cos\ ліворуч (k_x a\ праворуч) &= 0\ мітка {m0225_exbc2}\ -C\ cdot 0 + D\ cdot 1 &= 0\ мітка {m0225_exbc2}\ -C\ cdot 0 + D\ cdot 1 &= 0\ мітка {m0225_exbc2} 0225_EYBC1}\\ -C\ sin\ ліворуч (k_y b\ праворуч) + D\ cos\ ліворуч (k_y b\ праворуч) &= 0\ мітка {m0225_EYBC2}\ кінець {вирівнювання}

Рівняння\ ref {M0225_exbc1} і\ ref {M0225_EYBC1} можуть бути задоволені тільки якщо\(B=0\) і\(D=0\) відповідно. Згодом рівняння\ ref {m0225_exbc2} і\ ref {M0225_EYBC2} зводяться до:

\ begin {вирівняти}\ sin\ ліворуч (k_x а\ праворуч) &= 0\ мітка {m0225_exbc2a}\\ sin\ ліворуч (k_y b\ праворуч) &= 0\ етикетка {m0225_EYBC2a}\ кінець {вирівняти}

Для цього в свою чергу потрібно:

\ begin {вирівнювання} k_x &=\ гідророзриву {m\ pi} {a} ~, ~~~ m=0, 1, 2... \ етикетка {m0225_ekxm}\\ k_y &=\ розрив {n\ pi} {b} ~, ~~ n=0, 1, 2... \ етикетка {m0225_ekyn}\ кінець {вирівнювання}

Кожне натуральне ціле значення\(m\) і\(n\) призводить до коректного виразу,\(\widetilde{H}_z\) відомого як режим. Підводячи підсумки:

\[\widetilde{H}_z = \sum_{m=0}^{\infty} \sum_{n=0}^{\infty} \widetilde{H}_z^{(m,n)} \label{m0225_eEzTEall} \]

де

\[\widetilde{H}_z^{(m,n)} \triangleq H_0^{(m,n)} \cos\left(k_x x\right) \cos\left(k_y y\right) e^{-jk_z^{(m,n)} z} \widetilde{H}_z^{(m,n)} \triangleq H_0^{(m,n)} \cos\left(\frac{m\pi}{a} x\right) \cos\left(\frac{n\pi}{b} y\right) e^{-jk_z^{(m,n)} z} \label{m0225_eEzTE} \]

де\(H_0^{(m,n)}\) - довільна константа (консолідує константи\(A\) і\(C\)), і, так як\(k_x^2 + k_y^2 = k_{\rho}^2 \triangleq \beta^2-k_z^2\):

\[k_z^{(m,n)} = \sqrt{ \omega^2\mu\epsilon - \left(\frac{m\pi}{a}\right)^2 - \left(\frac{n\pi}{b}\right)^2 } \label{m0225_ekzm} \]

Підводячи підсумки:

Компонент TE (\(\widetilde{E}_z=0\)) односпрямованої (\(+\hat{\bf z}\)-біжучої) хвилі в прямокутному хвилеводі повністю визначається рівнянням\ ref {m0225_eezteAll} і складається з режимів, визначених рівняннями\ ref {m0225_eezte},\ ref {m0225_ekxm}, і\ ref {m0225_ekxm}, і\ ref {m0225_ekxm}. Решта ненульові компоненти поля можна визначити за допомогою Рівняння\ ref {M0225_Eexu} -\ ref {M0225_eHYU}.

Прийнято і зручно звертатися до режимів ТЕ в прямокутному хвилеводі, використовуючи позначення «ТЕ»\(_{mn}\). Наприклад, режим TE\(_{12}\) задається рівнянням\ ref {M0225_EEZTE} з\(m=1\) і\(n=2\).

Хоча Equation\ ref {M0225_EEZteAll} передбачає існування\(_{00}\) режиму TE, слід зазначити, що ця хвиля не має ненульових компонентів електричного поля. Це можна визначити математично, дотримуючись процедури, викладеної вище. Однак це також легко підтверджується наступним чином:\(\widetilde{E}_x\) є постійним для\(_{00}\) режиму TE, оскільки\(k_{\rho}=0\) для цього режиму, однак,\(\widetilde{E}_x\) повинен дорівнювати нулю, щоб відповідати граничним умовам на стінках при\(y=0\) і\(y=b\). Аналогічно,\(\widetilde{E}_y\) є постійним для\(_{00}\) режиму TE, однак,\(\widetilde{E}_y\) повинен дорівнювати нулю, щоб відповідати граничним умовам на стінках при\(x=0\) і\(x=b\).

Нарешті, зауважте, що значення,\(k_z^{(m,n)}\) отримані з Equation\ ref {m0225_ekzm}, не обов'язково є дійсними. Очевидно, що для будь-якого заданого значення\(m\),\(k_z^{(m,n)}\) буде уявним для всіх значень\(n\) більше, ніж деяке значення. Аналогічно, очевидно, що для будь-якого заданого значення\(n\),\(k_z^{(m,n)}\) буде уявним для всіх значень\(m\) більше, ніж деяке значення. Це явище є загальним як для TE, так і для TM компонентів, і тому розглядається в окремому розділі (Розділ 6.10).

Додаткове читання:

«Хвилевід (радіочастотний)» у Вікіпедії.
«Поділ змінних» у Вікіпедії.

Студентам рекомендується підтвердити, що вони правильні, підтвердивши, що вони є розв'язками рівнянь\ ref {m0225_ede5x} та\ ref {M0225_edE5x} відповідно. ↩