2.4: Закон Біот-Саварта

Закон Біот-Саварта (BSL) передбачає метод розрахунку магнітного поля за рахунок будь-якого розподілу сталого (постійного) струму. У магнітостатиці загальне рішення цієї проблеми використовує закон Ампера; т. Е.

$$\int_{\mathcal C} {\bf H} \cdot d{\bf l} = I_{encl} \nonumber$$

в цілісній формі або

$$\nabla \times {\bf H} = {\bf J} \nonumber$$

в диференційній формі. Інтегральна форма відносно проста, коли задача проявляє високий ступінь симетрії, полегшуючи простий опис в тій чи іншій системі координат. Прикладом може служити магнітне поле, обумовлене прямою і нескінченно довгою ниткою струму, яка легко визначається вирішенням інтегрального рівняння в циліндричних координатах. Однак багато проблем, що становлять практичний інтерес, не виявляють необхідної симетрії. Найпоширенішим прикладом є магнітне поле, обумовлене єдиним контуром струму, яке буде розглянуто в прикладі$\PageIndex{1}$. Для таких проблем потрібна диференціальна форма закону Ампера.

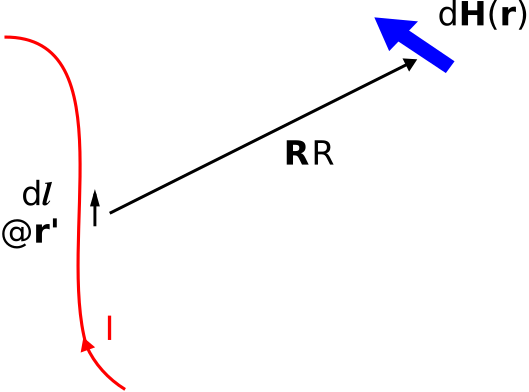
BSL - це розв'язання диференціальної форми закону Ампера для елемента струму диференціальної довжини, проілюстрованого на рис$\PageIndex{1}$. Поточний елемент - це$I~d{\bf l}$, де$I$ величина струму (СІ базові одиниці А) і$d{\bf l}$ являє собою диференціально-довжину вектор, що вказує напрямок струму в «вихідній точці»${\bf r}'$. Отриманий внесок в напруженість магнітного поля в «точці поля»${\bf r}$ становить

$$\boxed{ d{\bf H}({\bf r}) = I~d{\bf l}~\frac{1}{4\pi R^2} \times \hat{\bf R} } \label{m0066_eBS}$$

де

$${\bf R} = \hat{\bf R}R \triangleq {\bf r} - {\bf r}' \nonumber$$

Іншими словами,${\bf R}$ це вектор, що вказує від вихідної точки до точки поля, а$d{\bf H}$ в точці поля задається Equation\ ref {M0066_EBS}. Магнітне поле за рахунок струмоведучого проводу будь-якої форми може бути отримано шляхом інтеграції по довжині дроту:

$${\bf H}({\bf r}) = \int_{\mathcal{C}} d{\bf H}({\bf r}) = \frac{I}{4\pi} \int_{\mathcal{C}} \frac{d{\bf l}\times \hat{\bf R}}{R^2} \label{m0066_eBSI}$$

Малюнок$\PageIndex{1}$: Використання закону Біот-Саварта для обчислення магнітного поля за рахунок лінійного струму. (CC BY-SA 4.0; C Wang)

На додаток до усунення необхідності розв'язання диференціального рівняння, BSL надає деяке корисне уявлення про поведінку магнітних полів. Зокрема, Equation\ ref {M0066_EBS} вказує на те, що магнітні поля слідують закону зворотного квадрата — тобто величина магнітного поля внаслідок диференціального елемента струму зменшується пропорційно оберненому квадрату відстані ($R^{-2}$). Також Equation\ ref {M0066_EBS} вказує на те, що напрямок магнітного поля за рахунок диференціального елемента струму перпендикулярно як напрямку потоку струму, так$\hat{\bf l}$ і вектору, що$\hat{\bf R}$ вказує від вихідної точки до точки поля. Це спостереження є досить корисним для передбачення напрямку векторів магнітного поля в складних задачах.

Може бути корисним відзначити, що BSL є аналогом закону Кулона для електричних полів, який є розв'язком диференціальної форми закону Гауса,$\nabla \cdot {\bf D} = \rho_v$. Однак BSL застосовується тільки в магнітостатичних умовах. Якщо зміна струмів або магнітних полів з плином часу значна, то проблема значно ускладнюється. Див. розділ «Рівняння Єфіменка» у розділі «Додаткове читання» для отримання додаткової інформації.

Приклад$\PageIndex{1}$: Magnetic field along the axis of a circular loop of current

Розглянемо кільце радіуса$a$ в$z=0$ площині, зосереджене на початку координат, як показано на малюнку$\PageIndex{2}$.

Малюнок$\PageIndex{2}$: Розрахунок магнітного поля вздовж$z$ осі за рахунок кругового контуру струму, зосередженого в$z=0$ площині. (CC BY SA 4.0 (модифікований); К.Кіккері)

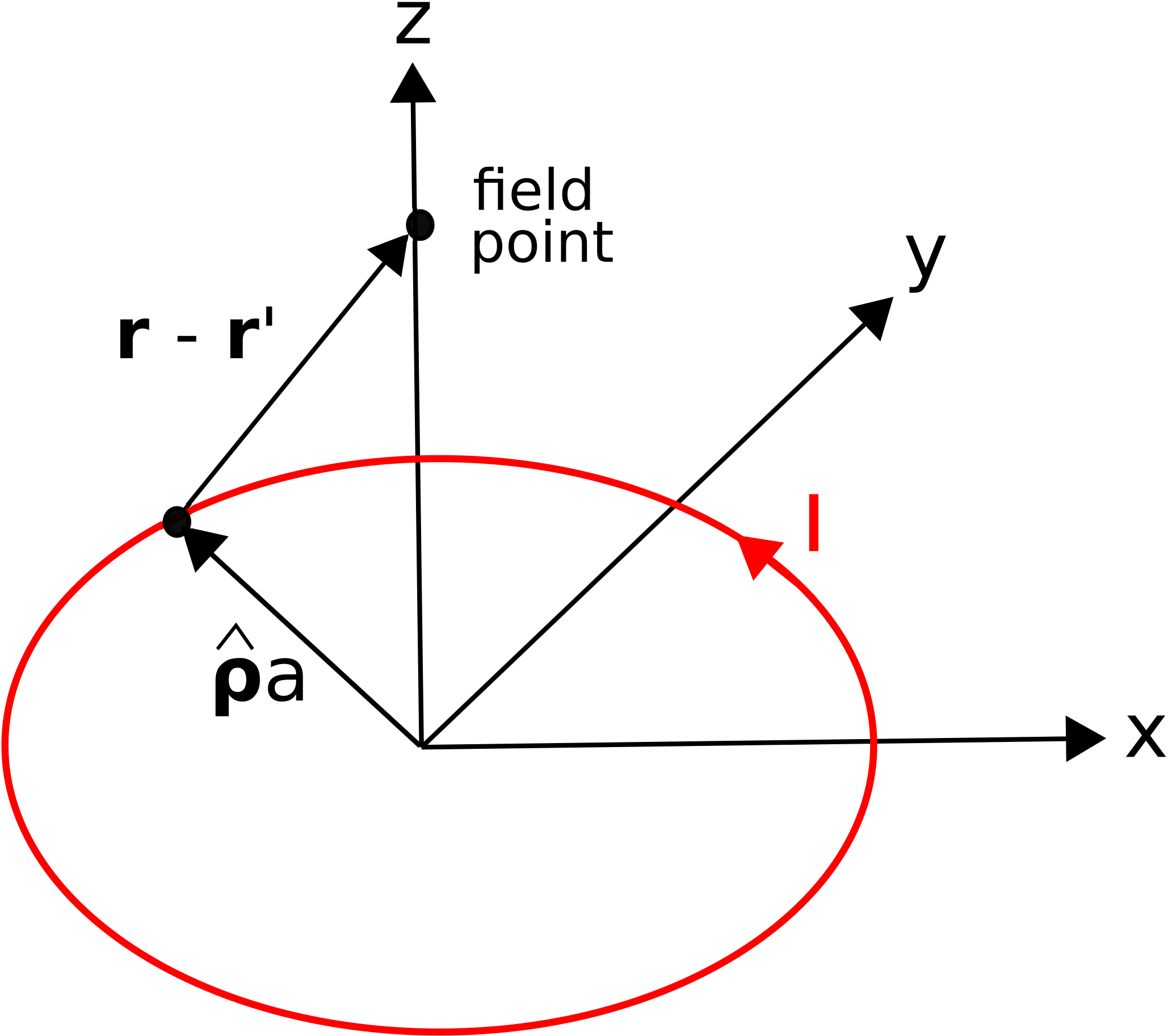
Як зазначено на малюнку, струм$I$ тече в$\hat{\bf \phi}$ напрямку. Знайдіть напруженість магнітного поля уздовж$z$ осі.

Рішення

Положення вихідного струму задається в циліндричних координатах як

$${\bf r}' = \hat{\bf \rho}a \nonumber$$

Положення точки поля вздовж$z$ осі дорівнює

$${\bf r} = \hat{\bf z}z \nonumber$$

Таким чином,

$$\hat{\bf R}R \triangleq {\bf r}-{\bf r}' = -\hat{\bf \rho}a + \hat{\bf z}z \nonumber$$

і

$$R \triangleq \left|{\bf r}-{\bf r}'\right| = \sqrt{a^2+z^2} \nonumber$$

Рівняння\ ref {M0066_EBS} стає:

$$\begin{aligned} d{\bf H}(\hat{\bf z}z) &= \frac{I~\hat{\bf\phi}~ad\phi}{4\pi \left[a^2+z^2\right]} \times \frac{\hat{\bf z}z-\hat{\bf \rho}a}{\sqrt{a^2+z^2}} \nonumber \\ &= \frac{Ia}{4\pi} ~ \frac{ \hat{\bf z}a-\hat{\bf \rho}z }{\left[a^2+z^2\right]^{3/2}} ~ d\phi\end{aligned} \nonumber$$

Тепер інтеграція над поточним:

$$\begin{aligned} &{\bf H}(\hat{\bf z}z) = \int_{0}^{2\pi} { \frac{Ia}{4\pi} ~ \frac{ \hat{\bf z}a - \hat{\bf \rho}z }{\left[a^2+z^2\right]^{3/2}} ~ d\phi }& \end{aligned} \nonumber$$

$$\begin{aligned} &= \frac{Ia}{4\pi \left[a^2+z^2\right]^{3/2}} \int_{0}^{2\pi} { \left( \hat{\bf z}a - \hat{\bf \rho}z \right) ~ d\phi }& \end{aligned} \nonumber$$

$$\begin{aligned} &= \frac{Ia}{4\pi \left[a^2+z^2\right]^{3/2}} \left( \hat{\bf z}a \int_{0}^{2\pi} { d\phi } -z \int_{0}^{2\pi} { \hat{\bf \rho} ~ d\phi }\right)&\end{aligned} \nonumber$$

Другий інтеграл дорівнює нулю. Щоб переконатися в цьому, зверніть увагу, що інтеграл просто підсумовує значення$\hat{\bf\rho}$ для всіх можливих значень$\phi$. Оскільки$\hat{\bf\rho}(\phi+\pi)=-\hat{\bf\rho}(\phi)$, integrand для будь-якого заданого значення$\phi$ дорівнює і протилежний цілим$\pi$ радіанам пізніше. (Це один із прикладів аргументу симетрії.)

Перший інтеграл в попередньому рівнянні дорівнює$2\pi$. Таким чином, отримуємо

$${\bf H}(\hat{\bf z}z) = \hat{\bf z}\frac{I a^2}{2\left[a^2+z^2\right]^{3/2}} \nonumber$$

Зверніть увагу, що результат узгоджується з пов'язаним «правилом правої руки» магнітостатики: Тобто напрямок магнітного поля знаходиться в напрямку згорнутих пальців правої руки, коли великий палець правої руки вирівнюється з розташуванням і напрямком струму. Це хороша вправа, щоб підтвердити, що цей результат також є правильним розмірами.

Рівняння\ ref {M0066_EBS} поширюється прямо на інші розподіли струму. Наприклад, магнітне поле, обумовлене поверхневим струмом${\bf J}_s$ (базові одиниці СІ А/м) можна обчислити за допомогою Equation\ ref {M0066_EBS} з$I~d{\bf l}$ заміненням на

$${\bf J}_s~ds \nonumber$$

де$ds$ - диференціальний елемент площі поверхні. Це може бути підтверджено розмірним аналізом:$I~d{\bf l}$ має SI базові одиниці A$\cdot$ m, як це робить${\bf J}_S~ds$. Аналогічно, магнітне поле, обумовлене об'ємним струмом${\bf J}$ (базові одиниці СІ А/м$^2$) можна обчислити за допомогою Equation\ ref {M0066_EBS} з$I~d{\bf l}$ заміненням на

$${\bf J}~dv \nonumber$$

де$dv$ - диференціальний елемент обсягу. Для однієї частинки із зарядом$q$ (SI базові одиниці С) та швидкістю${\bf v}$ (базові одиниці СІ м/с) відповідною величиною є

$$q{\bf v} \nonumber$$

оскільки C$\cdot$ м/с$=$ (C/s)$\cdot$ m = A$\cdot$ m У всіх цих випадках рівняння\ ref {M0066_EBS} застосовується з відповідною заміною на$I~d{\bf l}$.

Зверніть увагу, що величини$q{\bf v}$$I~d{\bf l}$,${\bf J}_S~ds$, і, всі${\bf J}~dv$, що мають однакові одиниці A$\cdot$ m, здається, мають на увазі одну і ту ж фізичну величину. Ця фізична величина відома як поточний момент. Таким чином, «вхід» в BSL можна інтерпретувати як поточний момент, незалежно від того, чи розподіляється цікавить струм як лінійний струм, поверхневий струм, об'ємний струм або просто як рухомі заряджені частинки. Див. «Додаткове читання» в кінці цього розділу для отримання додаткової інформації про поняття «момент» в класичній фізиці.

Додаткове читання:

• «Закон Біот-Саварта» у Вікіпедії.
• «Рівняння Єфіменко» у Вікіпедії.
• «Момент (фізика)» у Вікіпедії.