9.2: АНАЛІЗ

Для того щоб продемонструвати експлуатаційні особливості підсилювача, введені в попередньому розділі, необхідно аналітично наблизити деякі його більш важливі характеристики. Хоча точні деталі аналізу специфічні для цього підсилювача, кілька важливих особливостей, особливо тих, що стосуються динаміки та компенсації, є загальними для всіх двоступеневих операційних підсилювачів. Таким чином, висновки, до яких ми дійдемо, виходять за межі цієї конкретної схеми.

Слід розуміти, що деякі аспекти наступного аналізу, ймовірно, будуть помилковими в два або більше разів, оскільки невизначеність деяких значень параметрів, пов'язаних з транзисторами, обмежує точність. Інший тип складності зустрічається при аналізі динаміки підсилювача, так як в безпосередній близькості від використовуваних в підсилювачі транзисторів передбачається ряд полюсів.\(f_T\) Такі результати завжди підозрюються, оскільки недоліки транзисторної моделі перешкоджають точному аналізу в цьому діапазоні частот. На щастя, ці неточності не викликають занепокоєння, оскільки нашою метою є не стільки точне прогнозування продуктивності цього конкретного підсилювача, скільки розуміння важливих особливостей цього загального типу підсилювача.

Низькочастотний коефіцієнт посилення

Однією з важливих характеристик операційного підсилювача є його коефіцієнт посилення d-c розімкнутого контуру. Розрахунок коефіцієнта посилення цього підсилювача необхідний, оскільки точне вимірювання рівнів сигналу, що дозволило б експериментальне визначення посилення, виключається шумом та дрейфом.

На сьогоднішній день найбільша частка низькочастотного посилення підсилювача відбувається на стадії каскаду для цієї конкретної реалізації базової топології. Аналіз комплектного підсилювача полегшується спочатку розробкою низькочастотної еквівалентної схеми підсилювача каскоду. Аналіз розділу 8.3.4 показав, що посилення напруги ненавантаженого підсилювача каскаду дорівнює

\[-\dfrac{\beta_6}{2 \eta_6} = -\dfrac{g_{m6} r_{\mu 6}}{2}\nonumber \]

Малюнок 9.2 Еквівалентна схема для підсилювача каскаду на низьких частотах.

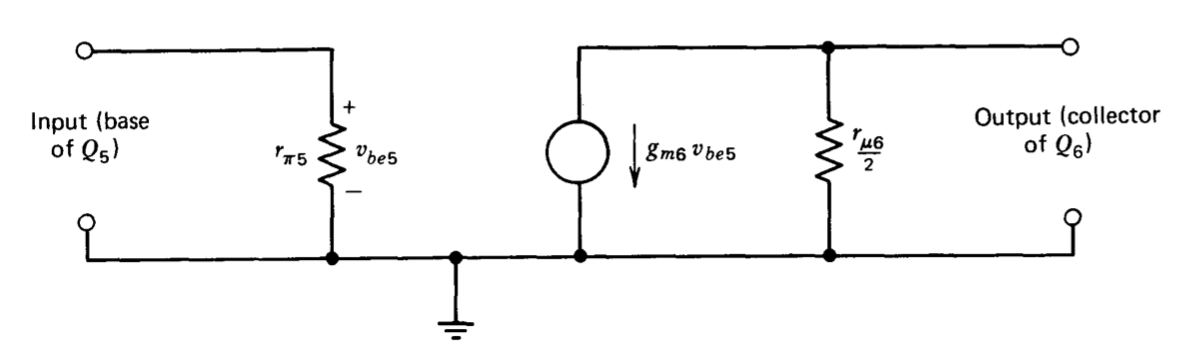
в той час як його вхідний опір є\(r_{\pi 5}\). (Індекси, що розрізняють два транзистори в підключенні каскаду, див. Рис. 9.1.) Поки вихідний опір підключення каскаду не було спеціально розраховано, для визначення цієї величини можна використовувати результат з розділу 8.3.5. Рівняння 8.3.47 дає\(r_{\mu} /2\) як вихідний опір джерела струму загальної основи з великим додатковим опором емітер-ланцюга. Вихідний опір каскода має бути ідентичним, так як його вихід складається із загального базового з'єднання з великим опором емітер-ланцюга. Ці результати показують, що низькочастотні показники частини каскаду підсилювача можуть бути змодельовані за допомогою еквівалентної схеми на малюнку 9.2.

Коефіцієнт посилення d-c схеми, показаної на малюнку 9.1, визначається за допомогою значень параметрів, наведених в таблиці 9.1 для транзисторів. Розрахунок виконується за умови, що неинвертирующий вхід підсилювача поступово заземлений. Це припущення дає те саме значення для посилення d-c, яке буде отримано з урахуванням справжньої диференціальної вхідної напруги. Поступово заземлення неінвертуючого входу усуває незначний високочастотний термін у передавальній функції, що виникає в результаті сигналів, що подаються через колектор-базову ємність\(Q_2\) (див. Розділ 8.2.3).

Таблиця 9.1 Транзисторні параметри для схеми малюнка 9.1

Номер транзистора	Тип	\(I_C\) або \(I_D\) (\(\mu A\))	\(g_m\) (ммхо)	\(\beta\)	\(r_{\pi}\) (\(k\Omega\))	\(r_{\mu}\) (\(k\Omega\))	\(r_{o}\) (\(k\Omega\))	\(C_{\mu}\) або \(C_{gd}\) (пФ)	\(C_{\pi}\) або \(C_{gs}\) (пФ)
\(Q_1, Q_2\)	2N5963	10	0.4	1100	2750	*	*	6	10
\(Q_3\)	2N3707	20	*	*	*	*	*	8	10
\(Q_4, Q_5, Q_6\)	2N4250	50	2	350	175	500	1.4	10	15
\(Q_7\)	2N3707	50	2	200	100	500	2.5	8	10
\(Q_8\)	ТІС 58	2 мА	*	-	-	-	-	2	*
\(Q_9\)	2N3707	2 мА	*	*	*	*	*	*	*
\(Q_{10}\)	2N2219	*	*	200	*	*	*	*	*
\(Q_{11}\)	2N2905	*	*	200	*	*	*	*	*
\(Q_{12}\)	2N3707	0	*	*	*	*	*	*	*
\(Q_{13}\)	2N4250	0	*	*	*	*	*	*	*

- Не актуально.
* Значення неважливе у включеному аналізі.

Загальний коефіцієнт посилення знаходить, спочатку обчислюючи передавальні відносини для різних ділянок ланцюга. Інкрементне вхідна напруга\(Q_1\)\(v_i\), прикладене до основи, викликає зміну струму колектора\(Q_2\) заданого

\[i_{c2} = -\dfrac{v_i g_{m1}}{2}\label{eq9.2.1} \]

(Передбачалося, що обидва вхідних транзистора працюють на рівних струмах так\(g_{m1} = g_{m2}\).)

Раніше розроблена схема еквівалентного каскаду показує, що зміна базової напруги\(Q_5\) пов'язане зі зміною\(Q_2\) колектор-струм на

\[v_{be5} = -i_{c2} (325 k\Omega || r_{\pi 5})\label{eq9.2.2} \]

(Потенціометр колектор-ланцюга вважається встановленим в центральне положення так, щоб резистор навантаження\(Q_2\) транзистора дорівнював\(325\ k\Omega\).) Для того щоб визначити коефіцієнт посилення напруги підсилювача каскакоду, необхідно розрахувати прикладену до нього навантаження. Вхідний опір польового\(Q_8\) транзистора по суті нескінченний, тоді як вихідний опір для джерела струму\(Q_7\) є

\[r_{\mu 7} \left | \right | \left [\dfrac{1 + g_{m7} (r_{\pi 7} || 68 k \Omega)}{g_{o7}} \right ] \nonumber \]

(Див. Рівняння 8.3.45.) Розрахунково зручно зменшити це рівняння зараз і ввести експериментально перевірене припущення, що\(r_{\mu 7} \simeq r_{\mu 6}\). Це значення є розумним, так як обидва пристрої працюють на однакових струмах, і виготовляються з використанням аналогічного (хоча і комплементарного) процесу ing. 2N3707 має\(\beta\) типовий 200 в\(50\ \mu A\), так\(r_{\pi 7}\) що, як правило,\(100\ k\Omega\) при цьому струму. Тому,\(r_{\pi 7} || 68 k\Omega \simeq 0.4r_{\pi 7}\). Відповідно, вихідний опір\(Q_7\) стає

\[r_{\mu 7} \left | \right | \left [\dfrac{1 + g_{m7} (0.4 r_{\pi 7})}{g_{o7}} \simeq r_{\mu 7} \left | \right | \left [ \dfrac{0.4 \beta_7}{g_{o7}} \right ] = r_{\mu 7} || 0.4 r_{\mu 7} \simeq 0.28 r_{\mu 7} \right ]\label{eq9.2.4} \]

Використовуючи цю залежність, передбачувана еквівалентність\(r_{\mu 7}\) і\(r_{\mu 6}\), а модель на малюнку 9.2 показує, що завантажений коефіцієнт посилення напруги каскаду дорівнює

\[\dfrac{v_{cb6}}{v_{be5}} \simeq -g_{m6} \left (\dfrac{r_{\mu 6}}{2} || 0.28 r_{\mu 6} \right ) \simeq -g_{m6} (0.18 r_{\mu 6} )\label{eq9.2.5} \]

Визнаючи, що ненавантажений посилення напруги від колектора\(Q_6\) до виходу підсилювача є одиницею і поєднує рівняння\(\ref{eq9.2.1}\)\(\ref{eq9.2.2}\), і\(\ref{eq9.2.5}\) дає

\[\dfrac{v_o}{v_i} = -\dfrac{g_{m1}}{2} (325 k\Omega || r_{\pi 5}) g_{m6} (0.18 r_{\mu 6}) \label{eq9.2.6} \]

Підстановка значень параметрів з таблиці 9.1 в рівняння\(\ref{eq9.2.6}\) прогнозує d-c величину посилення розімкнутого контуру\(4 \times 10^6\). У коефіцієнті посилення переважає внесок\(1.8 \times 10^5\) від підсилювача каскаду (див. Рівняння\(\ref{eq9.2.5}\)).

Функція передачі

Розташування всіх полюсів і нулів підсилювача можна було б передбачити для повної схеми, замінивши відповідні інкрементні моделі для активних пристроїв, хоча це було б грізним завданням навіть за допомогою комп'ютера. Підхід, який використовується тут, полягає в тому, щоб зробити відносно грубі наближення, щоб отримати уявлення про контрольну динаміку підсилювача, а потім перевірити приблизні результати за допомогою більш детального (хоча все ще неповного) комп'ютерного аналізу.

Вивантажений низькочастотний коефіцієнт посилення напруги буферного підсилювача (транзисторів\(Q_8\) через\(Q_{11}\)) дорівнює одиниці. Навантаження підсилювача аж до декількох сотень Ом не суттєво змінюють його продуктивність. Якщо навантаження, що подається на підсилювач, не є ємнісною, частотна характеристика буфера\(f_T\) наближається до використовуваних в ньому пристроїв. Крім того, вхідний опір\(Q_8\), який завантажує підсилювач каскаду, не залежить від будь-якого навантаження, що застосовується до виходу підсилювача, оскільки FET є одностороннім. Таким чином, вплив буфера можна моделювати, просто використовуючи вхідну ємність\(Q_8, C_{gd8}\), як навантаження для каскоду. Аналогічно навантаження транзистора\(Q_7\) можна представити у вигляді паралельного імпедансу, що складається з його вихідної ємності\(C_{\mu 7}\) і вихідного опору 0,28\(r_{\mu 7}\) (Рівняння\(\ref{eq9.2.4}\)).

Малюнок 9.3 Модель використовується для визначення передавальної функції.

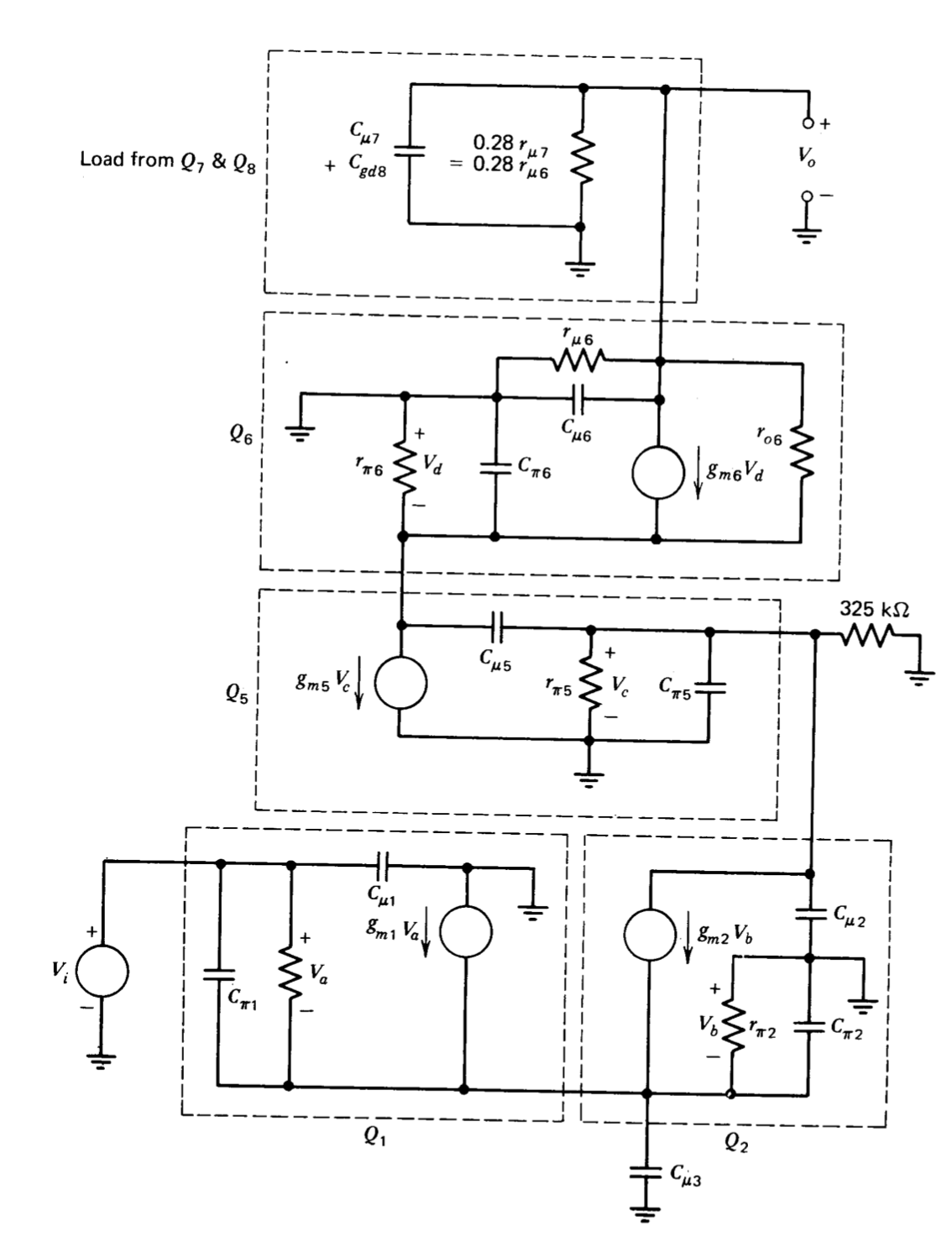
Інкрементна модель, яка відображає ці спрощення, показана на малюнку 9.3. Базові\(r_{\mu}\) опори\(r_o\) (\(r_x\)'и) всіх транзисторів, а також транзисторів, крім\(Q_6\) і\(Q_7\) (транзисторів у частині ланцюга з високим коефіцієнтом посилення) також були проігноровані. Для подальшого спрощення цієї моделі використовується аргумент, заснований на концепції постійних часу з відкритим контуром (див. П.Е. Грей і К.Л. Сірл, Електронні принципи: фізика, моделі та схеми, Wiley, New York, 1969, глави 15 і 16.). Опір розімкнутого ланцюга (Опір розімкнутого ланцюга, що стикається з конденсатором, - це додатковий опір на клемній парі, про яку йде мова, обчислюється з усіма іншими конденсаторами в ланцюзі знятими або розімкнутими.)\(C_{\pi 1}\), звернені до конденсаторів\(C_{\mu 1}\)\(C_{\pi 2}\),\(C_{\mu 3}\),, і\(C_{\pi 6}\) є все на замовлення\(1/g_m\), для відповідного транзистора або нижче. Таким чином, ці конденсатори не впливають на динаміку підсилювача на низьких частотах порівняно з різними транзисторами і усуваються для початкового наближення.\(f_T\) В результаті такого наближення єдиний внесок вхідного каскаду в динаміку підсилювача є наслідком навантаження\(C_{\mu 2}\) застосовується до бази\(Q_5\), а сам каскад може бути змодельований як єдине залежне джерело струму.

Малюнок 9.4 Спрощення малюнка 9.3.

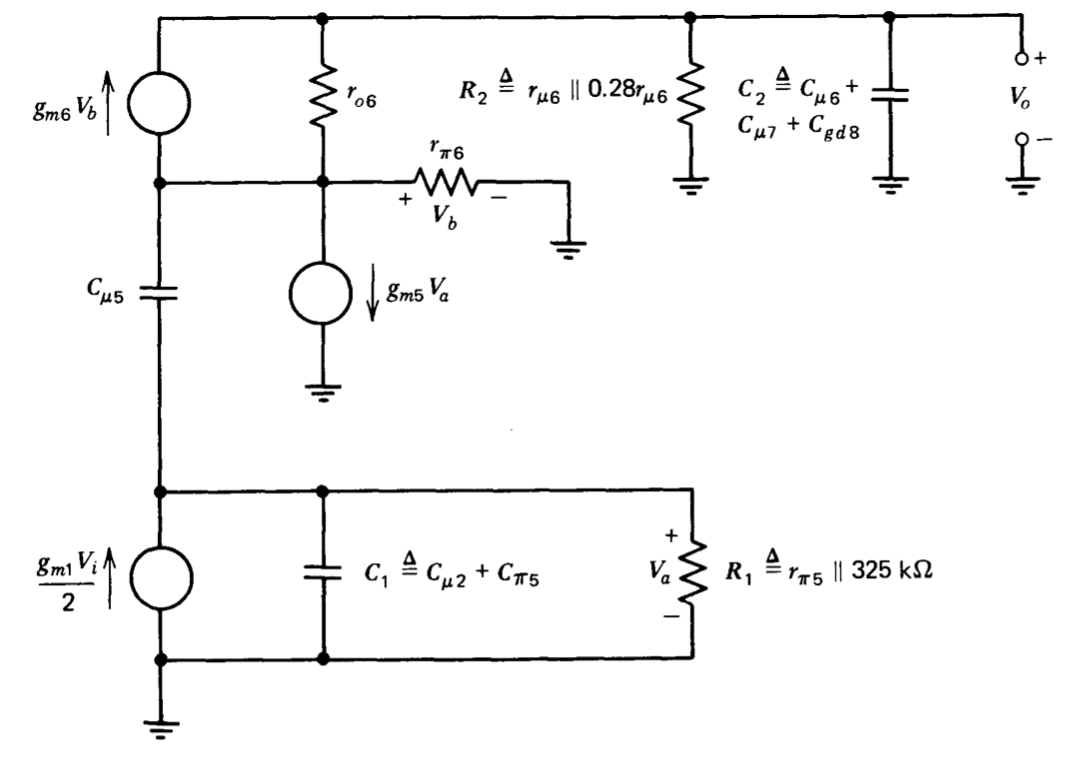
Подальше спрощена інкрементна модель, що включає наближення, наведені вище та показані на малюнку 9.4, використовується для наближення розташування двох полюсів підсилювача низької частоти. Рівняння вузлів для цієї схеми є

\[\begin{array} {rcl} {\dfrac{g_{m1} V_i}{2}} & = & {[(C_1 + C_{\mu 5}) s + G_1] V_a - C_{\mu 5} s V_b} \\ {0} & = & {(-C_{\mu 5} s + g_{m5})V_a + (C_{\mu 5} s + g_{m6} + g_{\pi 6} + g_{o 6}) V_b - g_{o6} V_o} \\ {0} & = & {(-g_{m6} - g_{o6})V_b + (C_2 s + g_{o6} + G_2)V_o} \end{array}\label{eq9.2.7} \]

(Див. Рис. 9.4 для визначення параметрів у цьому рівнянні.)

Полюси знаходять шляхом прирівнювання визначника матриці коефіцієнтів рівняння\(\ref{eq9.2.7}\) до нуля, що дає

\[\dfrac{C_1C_2C_{\mu 5}}{g_{m6} G_1 (G_2 + g_{\mu 6})} s^3 + \dfrac{C_2(C_1 + 2C_{\mu 5}}{G_1 (G_2 + g_{\mu 6})} s^2 + \dfrac{C_2}{C_2 + g_{\mu 6}} s + 1 = 0\label{eq9.2.8} \]

При скороченні рівняння\(\ref{eq9.2.7}\) до\(\ref{eq9.2.8}\), малі члени були скинуті. Однак лише терміни, які є невеликими через транзисторні та топологічні нерівності\(g_m \gg g_{\pi} \gg g_o \gg g_{\mu}\), такі як, і\(C_2 > C_{\mu 6}\) оскільки один компонент\(C_2\) є,\(C_{\mu 6}\) були усунені. Таким чином, висновки, які будуть зроблені з Рівняння,\(\ref{eq9.2.8}\) застосовні до різних схем, які поділяють цю топологію, а не обмежуються конкретним вибором значень елементів, показаних на малюнку 9.1. Фундаментальні відносини між значеннями параметрів також гарантують, що три полюси, представлені,\(\ref{eq9.2.8}\) будуть реальними та широко розставленими. Отже, це кубічне рівняння можна легко врахувати, так як

\[(\tau_a s + 1)(\tau_b s + 1) (\tau_c s + 1) \simeq \tau_a \tau_b \tau_c s^3 + \tau_a \tau_b s^2 + \tau_a s + 1 \text{ for } \tau_a \gg \tau_b \gg \tau_c \label{eq9.2.9} \]

Рівняння\(\ref{eq9.2.9}\) дозволяє нам записати рівняння\(\ref{eq9.2.8}\) як

\[\left (\dfrac{C_2}{C_2 + g_{\mu 6}} s + 1 \right ) \left (\dfrac{C_1 + 2C_{\mu 5}}{G_1} s + 1 \right ) \left (\dfrac{C_1C_{\mu 5}}{g_{m6} (C_1 + 2C_{\mu 5})} s + 1 \right ) = 0 \nonumber \]

вказуючи, що

\[\begin{array} {rcl} {\tau_a} & = & {\dfrac{C_2}{G_2 + g_{\mu 6}}} \\ {\tau_b} & = & {\dfrac{C_1 + 2C_{\mu 5}}{G_1}} \\ {\tau_c} & = & {\dfrac{C_1 C_{\mu 5}}{g_{m6} (C_1 + 2C_{\mu 5})}} \end{array} \label{eq9.2.11} \]

Фізична інтерпретація постійних часу дає розуміння роботи схеми. Опір, пов'язаний з постійною часу,\(\tau_a\) - це просто поступовий опір від вузла високого опору (колектора\(Q_6\)) до землі. [Нагадаємо\(1/(G_2 + g_{\mu 6}) =0.28r_{\mu 6} || r_{\mu 6} || r_{\mu 6} = 0.18r_{\mu 6}\), що значення, отримане раніше і використовується в Рівнянні\(\ref{eq9.2.5}\) для збільшення опору від цього вузла до землі.] Аналогічно ємність\(C_2 = C_{\mu 6} + C_{\mu 7} + C_{gd8}\) - це ємність від вузла високого опору до землі. Оскільки ємність всіх вузлів підсилювача однакового порядку, не дивно, що домінантний полюс підсилювача пов'язаний з накопиченням енергії на самому високому вузлі опору. Підставляючи значення з таблиці 9.1, видно\(\tau_a = 1.8\ ms\), що, маючи на увазі, що домінантний полюс відкритого контуру підсилювача розташований за адресою\(s = - 550\text{ sec}^{-1}\).

Постійна часу\(\tau_b\) пов'язана з опором і ємністю від основи\(Q_5\) до землі. Провідність\(G_1\) у рівнянні\(\ref{eq9.2.11}\) була визначена раніше як провідність від цього вузла до землі. Ємність складається з ємності колектора до бази,\(Q_2\) що шунтує цей вузол, і загальна ефективна вхідна ємність (включаючи ту, що приписується ефекту Міллера)\(Q_5\) буде відображатися, якби цей транзистор був завантажений резистивним навантаженням, рівним\(1/g_{m5}\). Відзначимо, що на частотах набагато вище\(1/\tau_a\) радіанів в секунду ємнісне навантаження на колекторі з\(Q_6\) зменшило посилення напруги цього транзистора; в результаті на цих частотах немає значного зворотного зв'язку з емітером\(Q_6\)\(r_{o6}\) наскрізних. Таким чином транзистор\(Q_6\) забезпечує\(1/g_{m6} = 1/g_{m5}\) навантаження для\(Q_5\). Постійна часу rb дорівнює\(4.5\ \mu s\), маючи на увазі, що другий полюс підсилювача розташований за адресою\(s = -2.2 \times 10^5 \text{ sec}^{-1}\). Постійна часу\(\tau_c\) відповідає частоті, яка наближається\(f_T\) для транзисторів в ланцюзі, і, таким чином, одному з багатьох високочастотних полюсів, які ігноруються в спрощеному аналізі.

Поєднання коефіцієнта посилення d-c (Equation\(\ref{eq9.2.6}\)) з динамікою прогнозованої вище врожайності

\[\dfrac{V_o (s)}{V_i (s)} = \dfrac{-4 \times 10^6}{(1.8 \times 10^{-3} s + 1)(4.5 \times 10^{-6} s + 1)}\label{eq9.2.12} \]

Малюнок 9.5 Функція передачі розімкнутого контуру підсилювача на основі двох полюсів найнижчої частоти (без компенсації).

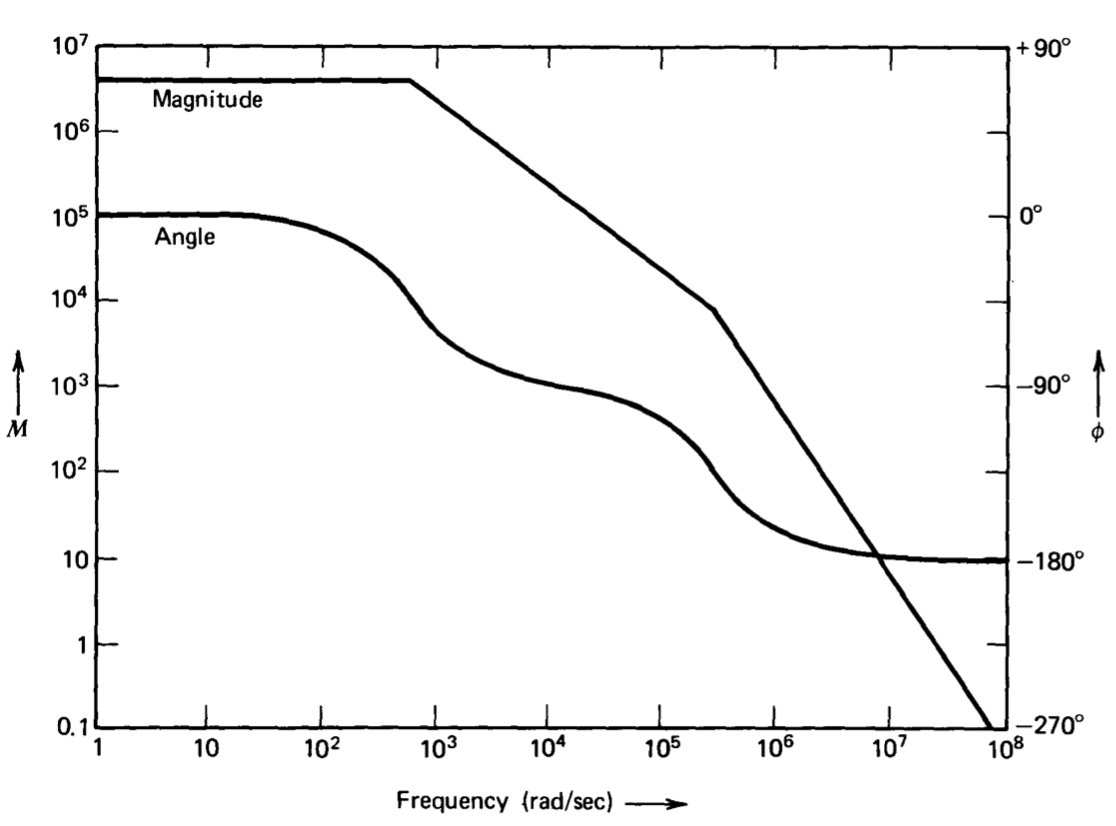
\(\ref{eq9.2.12}\)Рівняння показано у вигляді графіка Боде (Передавальна функція, побудована на малюнку 9.5, насправді є негативною від Рівняння\(\ref{eq9.2.12}\). Ця модифікація зроблена тому, що ми передбачаємо використання підсилювача в з'єднаннях з негативним зворотним зв'язком. Оскільки передача петлі має той же знак, що і коефіцієнт посилення, розрахований для підсилювача в цих додатках, побудова негативу посилення підсилювача слідує умові побудови негативу передачі петлі системи зворотного зв'язку. Розглядається альтернативно, функція передачі, побудована на малюнку 9.5, призведе до того, що вхідний сигнал був застосований до неінвертуючого вхідного терміналу підсилювача.) на малюнку 9.5.

Місця полюсів для цієї конструкції також були передбачені комп'ютерним аналізом sis, для того, щоб перевірити деякі припущення, введені в попередній розробці. Проаналізовано еквівалентну схему малюнка 9.3 з\(100-\Omega\) базовими резисторами, доданими до моделі схеми для кожного транзистора. Таким чином, тільки буферний підсилювач був виключений з обчислень комп'ютера. Місця двох домінуючих полюсів, передбачених комп'ютером, були\(- 520\text{ sec}^{-1}\) і\(- 2.15 \times 10^5\text{ sec}^{-1}\). Всі інші полюси мали частоти розриву понад\(10^7\) радіанів в секунду. Незважаючи на здавалося б кардинальні наближення, включені в аналіз цієї схеми, прогнозовані місця розташування двох домінантних полюсів підтверджуються комп'ютерним розрахунком з точністю до похибок округлення.

Метод компенсації

Передавальна функція цього підсилювача (Equation\(\ref{eq9.2.12}\)) має полюси, розділені коефіцієнтом 400, і в багатьох підсилювачах зворотного зв'язку ця величина поділу здавалася б ідеальною з точки зору стабільності. На жаль, з масивним низькочастотним коефіцієнтом посилення розімкнутого контуру, характерним для операційних підсилювачів (\(4 \times 10^6\)у цій конструкції), для забезпечення адекватної стабільності в багатьох додатках потрібно більше розділення. Наприклад, якщо підсилювач використовується в якості послідовного коефіцієнта посилення, підключивши його вихід до його інвертуючого входу, утворюється петля з таким,\(a(j\omega )\) як показано на малюнку 9.5 і\(f = 1\). Графік Боде показує, що фазовий запас системи приблизно\(0.5^{\circ}\) в цьому випадку явно незадовільний. На практиці ця конфігурація була б нестабільною, оскільки негативний зсув фаз, пов'язаний із нехтованими особливостями відкритого циклу, набагато більший, ніж\(0.5^{\circ}\) на частоті посилення одиниці підсилювача. Зрозуміло, що для модифікації функції передачі підсилювача з розімкнутим контуром необхідно використовувати певний метод, щоб досягти прийнятної продуктивності в цьому та багатьох інших з'єднаннях.

Однією з суттєвих переваг конфігурації підсилювача, описаної в цьому розділі, та всіх підсилювачів, які поділяють його топологію, є те, що можна використовувати внутрішній зворотний зв'язок для забезпечення легко прогнозованої та добре керованої компенсації. Компенсація реалізується шляхом підключення мережі між клемами з позначкою компенсації на малюнку 9.1. Ця мережа завершує незначний цикл, який включає етап з високим коефіцієнтом посилення. Оскільки обидва домінуючі полюси підсилювача включені всередині локального контуру зворотного зв'язку, можна змінити розташування найважливіших полюсів у функції передачі підсилювача за допомогою цього типу внутрішнього зворотного зв'язку. Ступінь контролю, яку може здійснювати зворотний зв'язок із незначним контуром на передавальну функцію двоступеневого підсилювача, натякав у розділі 5.3 та в обговоренні ефектів каскаду\(C_{\mu}\) з високим коефіцієнтом посилення в розділі 8.2.3.

Існує як мінімум два важливих обмеження для цього виду компенсації. По-перше, оскільки ця компенсація є формою негативного зворотного зв'язку, величина компенсованої передавальної функції підсилювача з розімкнутим контуром буде менше або дорівнює величині некомпенсованої передавальної функції на більшості частот. Хоча резонанси, введені незначним контуром зворотного зв'язку, можуть дати збільшення посилення на одній або двох конкретних частотах, смуга пропускання, над якою існують такі збільшення, обов'язково обмежена. По-друге, існує деяка максимальна частота, для якої це ефективний метод компенсації, оскільки поза цією частотою вплив інших особливостей, деякі з яких знаходяться поза компенсуючим контуром і тому не можуть контролюватися, стає важливим. Хоча ці особливості всі на частотах, порівнянних з транзисторами, вони встановлюють граничне обмеження пропускної здатності підсилювача через зсув фаз, що вони сприяють його функції передачі відкритого контуру на частотах, що представляють інтерес.\(f_T\) Наприклад, на 1/10 його частоти розриву полюс 10-го порядку сприяє негативному зсуву\(57^{\circ}\) фаз до передавальної функції, але змінює величину лише на 5%. На практиці частота одиниці-посилення комбінації мережі підсилювача зворотного зв'язку зазвичай вибирається для обмеження фазового внеску високочастотних сингулярностей менше, ніж\(30^{\circ}\) на цій частоті, щоб стабільність не була порушена. Часто доводиться визначати частоту, з якою фазовий зсув особливостей вищого порядку стає важливим експериментальним шляхом через труднощі, пов'язані з точним аналітичним прогнозом їх розташування.

Малюнок 9.6 Модель використовується для ілюстрації методу компенсації.

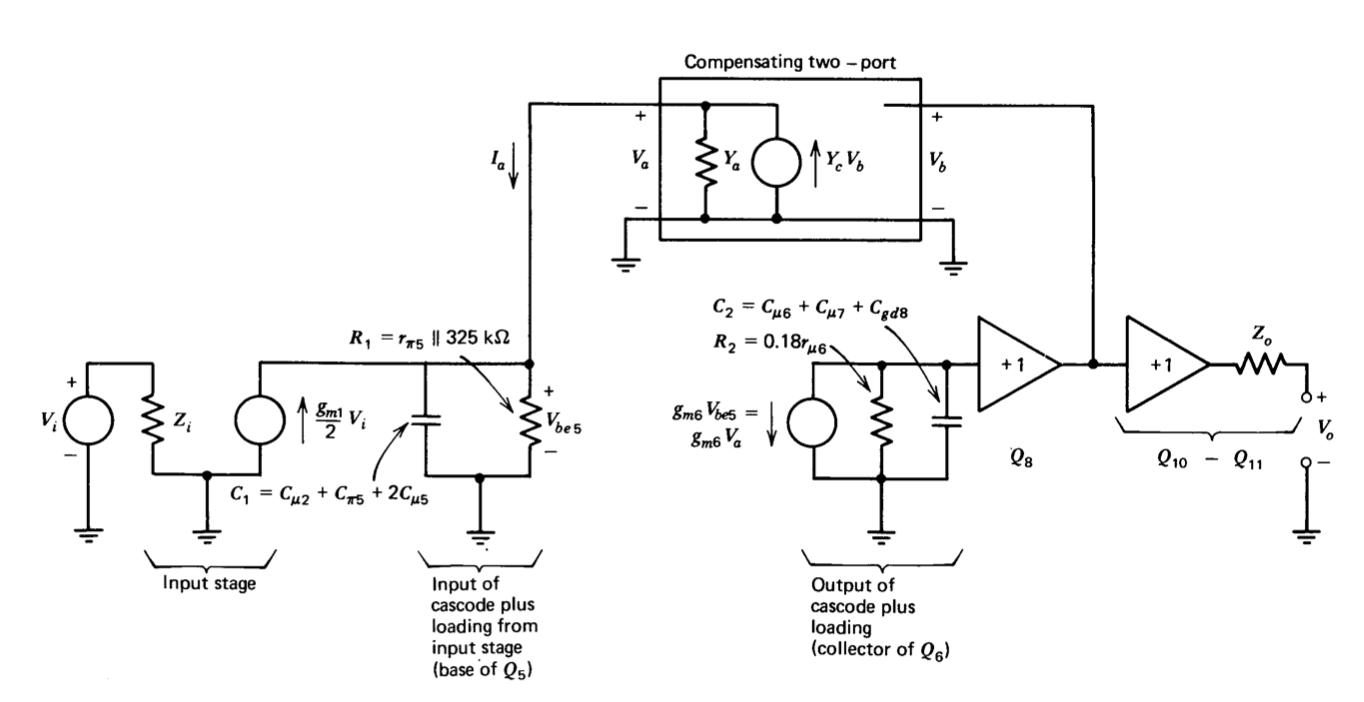
Інкрементна модель підсилювача малюнка 9.1, яка може бути використана для аналізу ефектів внутрішнього зворотного зв'язку, використовуваного для компенсації, показана на малюнку 9.6. Розробка цієї моделі значною мірою спирається на аналіз Розділу 9.2.2. Вхідний опір підсилювача, який не важливий для цілей цього розрахунку, є\(Z_i\). Вхідна напруга змушує пропорційний струм на вузлі, включаючи базу\(Q_5\). (Це подання передбачало вхідну напругу, прикладену до інвертуючого входу підсилювача. Якщо напруги подаються на обидва входи, використовується диференціальна напруга для\(V_i\). Перевагою цього типу підсилювача є те, що динаміка першого ступеня істотно не впливає на передавальну функцію на частотах, що цікавлять; таким чином він функціонує як справжній диференціально-вхідний підсилювач.)

Імпеданс в основі\(Q_5\) моделюється як паралельна\(R-C\) мережа з постійною часу, рівною рівнянню\(\ref{eq9.2.11}\).\(\tau_b\) Залишок каскаду моделюється як імпеданс, рівний імпедансу від колектора\(Q_6\) до землі, приводиться в дію залежним джерелом струму, що подає струм\(g_{m6} V_{be5}\). Перетворення імпедансу польового транзистора представляється як буферний підсилювач одиниці напруги посилення. Додаткова пара емітер-послідовник моделюється як другий буферний підсилювач з вихідним імпедансом\(Z_o\).

Компенсуючий незначний контур утворюється шляхом підключення двопортової мережі між виходом послідовника джерела і базою\(Q_5\). Оскільки правий порт мережі приводиться в дію послідовником джерела низького імпедансу,\(V_b\) напруга не залежить від\(V_a\); Таким чином, два порти можуть бути повністю представлені в цій програмі двома допусками (Ці визначення відрізняються від тих, які умовно використовуються для опису двох портів мереж в тому, що орієнтовний напрямок для\(I_a\) знаходиться поза мережею. Цей вибір зменшує кількість знаків мінуса в наступних рівняннях.)

\[Y_a = -\dfrac{I_a}{V_a} \ \ \ V_b = 0 \nonumber \]

\[Y_c = -\dfrac{I_a}{V_b} \ \ \ V_a = 0 \nonumber \]

Вузлові рівняння для моделі рисунка 9.6

\[\begin{array} {rcl} {\dfrac{g_{m1}}{2} V_i} & = & {(Y_1 + Y_a) V_a - Y_c V_b} \\ {0} & = & {g_{m6} V_a + Y_2 V_b}\label{eq9.2.15} \]

де

\[Y_1 = \dfrac{1}{R_1} + C_1 s \nonumber \]

\[Y_2 = \dfrac{1}{R_2} + C_2 s \nonumber \]

Визнання того, що вихідна напруга\(V_o\) ідентична при відсутності навантаження дозволяє визначити коефіцієнт посилення підсилювача з Рівняння\(\ref{eq9.2.15}\) як\(V_b\)

\[\dfrac{V_o}{V_i} = \dfrac{V_b}{V_i} = -\dfrac{(g_{m1}/2) g_{m6}/[(Y_1 + Y_a) Y_2]}{1 + g_{m6} Y_c/[(Y_1 + Y_a) Y_2]}\label{eq9.2.16} \]

передача внутрішнього контуру, що утворюється при компенсації підсилювача. У багатьох випадках, що представляють практичний інтерес, фазовий кут цього виразу близький до плюс-мінус,\(90^{\circ}\) коли його величина дорівнює одиниці. Запас\(90^{\circ}\) фази компенсуючого контуру тоді гарантує, що в його відгуку немає піку. У цих випадках дуже просте наближення служить для визначення величини передавальної функції підсилювача з розімкнутим контуром, і наближення дає результат, правильний в межах коефіцієнта 0,707 на всіх частотах. Імплікація з\(\ref{eq9.2.16}\) полягає в тому, що

\[\dfrac{V_o (j\omega)}{V_i (j\omega)} \simeq - \dfrac{g_{m1}}{2Y_c (j\omega )}\label{eq9.2.17} \]

на частотах, де

\[\left |\dfrac{g_{m6} Y_c (j\omega )}{[Y_1 (j\omega ) + Y_a (j\omega )] Y_2 (j\omega )} \right | > 1\nonumber \]

і

\[\dfrac{V_o (j\omega )}{V_i (j\omega )} \simeq -\dfrac{g_{m1}}{2} \dfrac{g_{m6}}{[Y_1 (j\omega ) + Y_a (j\omega )] Y_2 (j\omega )}\label{eq9.2.18} \]

на всіх інших частотах. Таким чином, коли величина передачі незначного контуру велика, функція передачі в розімкнутому контурі підсилювача управляється елементом зворотного зв'язку з незначним контуром.

Це наближення особливо легко застосувати графічно. Функція передачі розімкнутого контуру підсилювача без компенсації, але з компенсуючим мережевим навантаженням бази\(Q_5\), побудована на координатах довгої величини проти довгочастотних координат. Правильна завантаження реалізується шляхом підключення однієї сторони мережі до бази звичайним способом, а також шляхом відключення іншої сторони мережі від джерела\(Q_8\) і підключення її замість цього до інкрементного заземлення.\(Q_5\) Цей перший графік особливо легко отримати, якщо один конденсатор використовується як компенсуючий елемент (найчастіший випадок, оскільки ця компенсація призводить до приблизно однополюсної функції передачі з відкритим контуром), оскільки змінюється лише розташування полюса більш високої частоти в\(\ref{eq9.2.12}\) Рівнянні. Величина виразу також\(g_{m1}/2 Y_e(j\omega )\) наноситься на ті ж координати. Величина функції передачі розімкнутого контуру підсилювача на будь-якій частоті тоді приблизно дорівнює меншій величині двох побудованих кривих. Цей зв'язок легко розвивається з Рівняння\(\ref{eq9.2.17}\) і\(\ref{eq9.2.18}\), помітивши, що коефіцієнт посилення підсилювача з закороченою компенсуючою мережею, підключеним до основи,\(Q_5\) є

\[\dfrac{g_{m1}}{2} \dfrac{g_{m6}}{(Y_1 + Y_a) Y_2}\nonumber \]

і що якщо

\[\left | \dfrac{g_{m1}}{2Y_c} \right | < \left | \dfrac{g_{m1}}{2} \dfrac{g_{m6}}{(Y_1 + Y_a) Y_2} \right |\nonumber \]

потім

\[\left | \dfrac{g_{m6} Y_c}{(Y_1 + Y_a) Y_2} \right | > 1\nonumber \]

Малюнок 9.7 Ефект компенсації.

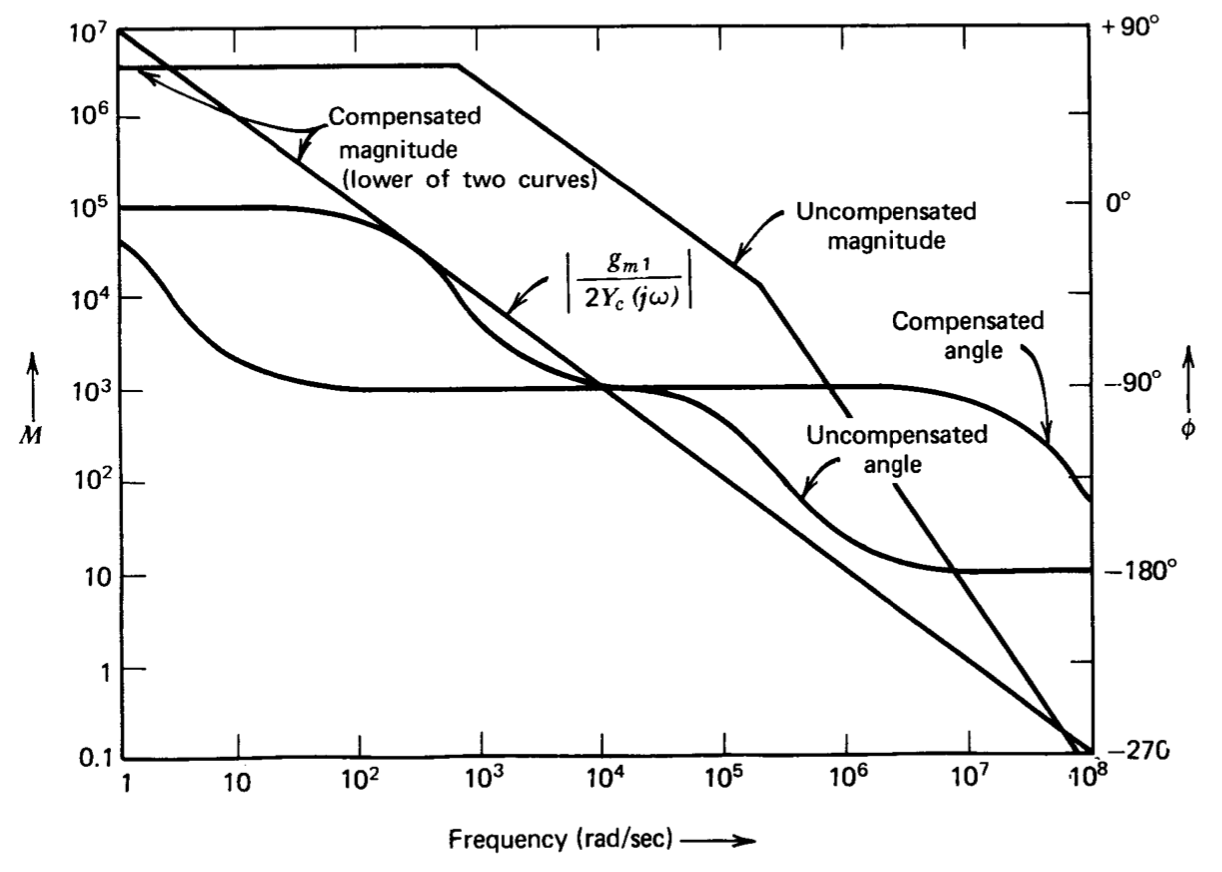
Малюнок 9.7 ілюструє ефекти компенсації підсилювача, показані на малюнку 9.1 конденсатором 20-пФ. Кількість\(Y_c\) і\(Y_a\) для цієї мережі compen sating обидва рівні\(2 \times 10^{-11}s\). Одна з двох кривих виходить безпосередньо з некомпенсованої передавальної функції рис. 9.5 шляхом переміщення другого полюса з\(2.2 \times 10^5\)\(1.5 \times 10^5\) радіанів в секунду в радіани в секунду, так як навантаження компенсуючим конденсатором збільшує загальну ємність біля основи\(Q_5\) на 50%. Другий сюжет

\[\left | \right | = \dfrac{10^7}{\omega } \nonumber \]

Крива для компенсованого підсилювача - нижня з двох графіків на всіх частотах.

Переваги цієї компенсації при певних додатках очевидні. Раніше було показано, що робота з\(f = 1\) призведе до коливання підсилювача з компенсацією. Якщо використовується компенсаційний конденсатор на 20 пФ, то запас фази підсилювача з прямим зворотним зв'язком більше\(45^{\circ}\).

Зверніть увагу, що ця компенсація знижує перший полюс відкритого контуру підсилювача до 2,5 радіанів в секунду. Розташування низькочастотного полюса не можна вибрати самостійно, якщо наполягати на однополюсному відкаті на частотах

нижче частоти посилення одиниці та обмежують як одиничну частоту посилення, так і коефіцієнт посилення d-c. Полюс повинен розташовуватися на частоті, рівній відношенню частоти одиниці-посилення до коефіцієнта посилення d-c. Цей полюс не компрометує смугу пропускання замкнутого циклу, оскільки смуга пропускання замкнутого циклу визначається частотою кросовера контуру.

Варто згадати, що значення параметрів для цього підсилювача такі, що некомпенсована функція передачі розімкнутого контуру буде помітно змінена будь-якою ємнісною компенсацією, що перевищує приблизно 0,1 пФ! Мінімальне значення конденсатора, необхідне для модифікації передавальної функції підсилювача, можна визначити, зазначивши, що крива некомпенсованої величини, показана на малюнку 9.5, включає область, де її значення.\(2 \times 10^9/\omega \) Таким чином, якщо для компенсації використовується конденсатор, що перевищує 0,1 пФ, величина\([g_{m1}/2 Y_c(j\omega )\) буде бути меншим, ніж некомпенсована величина в деякому діапазоні частот. Крім того, очевидно, що зворотний зв'язок від будь-якої частини ланцюга високого рівня (від колектора\(Q_6\) включення) назад до базової схеми Q5 має приблизно такий же ефект, як зворотний зв'язок через компенсаційні клеми. Неминуча бродяча ємність між цими двома частинами ланцюга зазвичай знаходиться на порядку 1 пФ, і тому робиться висновок, що «некомпенсована» крива на малюнку 9.7, ймовірно, ніколи не може бути виміряна для фактичного підсилювача.

Як зазначено вище, зворотний зв'язок від будь-якої частини схеми від колектора\(Q_6\) на модифікує продуктивність приблизно так само, як і зворотний зв'язок від джерела\(Q_8\), і в деяких додатках це може бути вигідно компенсувати подачею назад з альтернативної точки. Наприклад, зворотний зв'язок від вихідного терміналу включає більше підсилювача всередині компенсуючого контуру і, таким чином, з керуванням цим контуром. На жаль, стабільність компенсаційного контуру менш визначена для цього типу зворотного зв'язку з незначним контуром. Аналогічно, якщо для компенсації використовуються великі конденсатори, більша стабільність внутрішнього контуру може бути досягнута компенсацією від колектора\(Q_6\).

Деякі причини вибору топології підсилювача з можливістю такого типу компенсації тепер повинні бути зрозумілими. Компенсація зазвичай вибирається так, що вона, а не некомпенсована динаміка підсилювача, домінує в продуктивності підсилювача на всіх частотах, що цікавлять. Таким чином, функція передачі розімкнутого контуру підсилювача з компенсацією стає досить надійною. Можна отримати найрізноманітніші функції передачі з розімкнутим контуром (кілька прикладів будуть наведені в главі 13), при цьому основним обмеженням є вимога збереження стійкості компенсуючого контуру. Крім того, легко визначити, яку компенсуючу мережу слід використовувати для отримання заданої функції передачі з розімкнутим контуром.