Skip to main content
LibreTexts - Ukrayinska

6.8: Поліацетилен

  1. Last updated
  2. Save as PDF
  • Page ID
    31798

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Далі розглянемо більш довгу ланцюжок атомів вуглецю. Дуже довгі молекули відомі як полімери, а полімерний еквівалент ідеалізованого провідника на малюнку\(\PageIndex{1}\) відомий як поліацетилен.

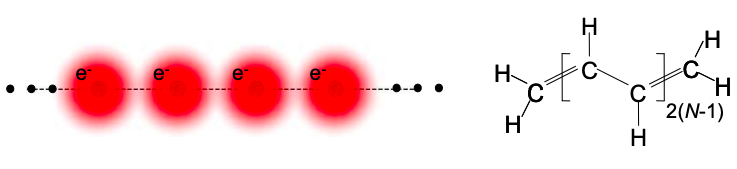
    Знімок екрана 2021-05-24 о 20.34.40 pn
    Малюнок\(\PageIndex{1}\): (ліворуч) Нескінченний ланцюг атомів, кожен з яких сприяє одному електрону в прикордонній орбіталі. (Праворуч) Еквівалентний полімерний поліацетилен.

    Зокрема, давайте вирішимо для вуглецевого ланцюга атомів N. Рівняння (6.8.11) є прикладом тридіагонального детермінанта. Загалом тридіагональний детермінант N × N має власні значення:\(^{†}\)

    \[ E_{n}= \alpha+2\beta \cos\left( \frac{n\pi}{N+1}\right), n = 1,2,…N. \nonumber \]

    та власні вектори:

    \[ c_{j} = \sin\left( jn\frac{\pi}{N+1} \right), \ \ j, n = 1,2,… N. \nonumber \]

    Зверніть увагу, що Рівняння. (6.9.1) - (6.9.2) зводяться до рівнянь. (6.8.11) - (6.8.12) за допомогою ідентичності:\(\cos\left(2\pi/5\right)=1/4\left(-1+\sqrt{5}\right)\)

    Таким чином, ми вирішили молекулярні орбіталі в молекулі, змодельованої довільно довгим ланцюгом прикордонних атомних орбіталів, кожна з яких містить один електрон.

    Далі давайте повторно висловимо наші розчини для поліацетилену в терміні хвильового вектора, k. Зверніть увагу, що оскільки атоми дискретно розташовані в ланцюжку, k також дискретний. Є тільки N допустимих значень k.

    З огляду на\(x = ja_{0}\), де\(a_{0}\) знаходиться відстань між атомами вуглецю, отримаємо:

    \[ c(x) = \sin(kx) \nonumber \]

    і

    \[ E_{n} = \alpha+2\beta \cos(ka_{0}) \nonumber \]

    де

    \[ k = \frac{\pi}{a_{0}} \frac{n}{N+1}, \ \ n=1,2,…N \nonumber \]

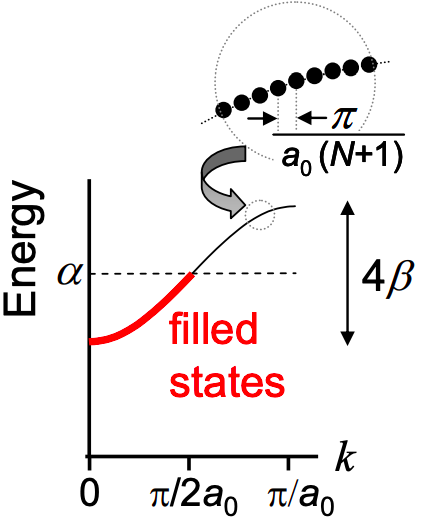
    Дисперсійне співвідношення поліацетилену побудовано на малюнку 6.9.2. Енергетичні стани обмежуються енергіями, що\[ E = \alpha \pm 2\beta , \nonumber \] утворюють смугу, ширини\(4\beta\), зосередженої на\(\alpha\). Пропускна здатність (\(4\beta\)) безпосередньо пов'язана з стрибковою взаємодією між сусідніми атомами вуглецю. Це загальна властивість: чим сильніше взаємодія між електроном і сусідніми атомами, тим більше пропускна здатність. І як ми будемо, чим ширше електронна смуга пропускання, тим краще електронна провідність всередині матеріалу.

    У смузі є N станів, кожне розділене

    \[ \Delta k = \frac{\pi}{a_{0}(N+1)} \nonumber \]

    Зверніть увагу, що довжина ланцюга дорівнює\(L = (N-1)a_{0}\). Таким чином, для довгих ланцюгів поділ між станами в смузі приблизно

    \[ \Delta k \approx \frac{\pi}{L} \nonumber \]

    Тепер кожен атом вуглецю вносить один електрон в прикордонних атомних орбіталів, які складають молекулярні орбіталі. Таким чином, для N-повторного полімеру існує N електронів. Але кожен стан тримає два електрони, по одному з кожного спина. Заповнюючи спочатку найнижчі енергетичні стани, заповнюються тільки перші N/2 k стани; див. Рис. 6.17. Таким чином, смуга заповнена лише наполовину, і тому, якщо полімер був підключений до контактів, ми могли б очікувати, що поліацетилен буде металом.

    Скріншот 2021-05-25 о 16.26.06.png
    Малюнок\(\PageIndex{2}\): Дисперсійне співвідношення поліацетилену, визначене аналізом щільного зв'язування. Для атомів N, кожен з яких дарує один електрон у прикордонній атомній орбіталі, існує N молекулярних орбіталів з енергіями, розташованими в смузі. Оскільки смуга держав заповнена лише наполовину, цей матеріал може бути металом.

    \(^{†}\)Якщо ви зацікавлені і маєте кілька вільних годин, ви можете спробувати це довести. Оцінивши кілька перших детермінант простих тридіагональних матриць, N=1, N=2, N=3 тощо знаходять і розв'язують різницеве рівняння для детермінант як функції матричної розмірності, N.