1.31: Проблеми

1. Припустимо, ми запалюємо електрони через єдину щілину шириною d. На екрані перегляду за діафрагмою електрони сформують візерунок. Виведіть та намалюйте вираз для інтенсивності на екрані перегляду. Викладіть всі необхідні припущення.

Рисунок$\PageIndex{1}$: Геометрія експерименту з дифракцією однієї щілини.

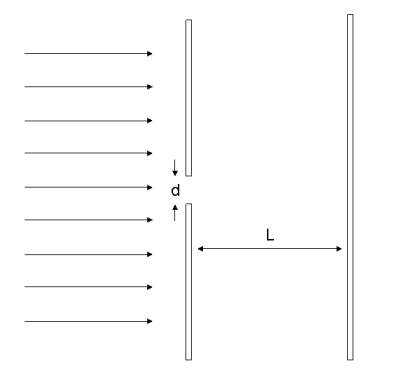
Чим цей візерунок відрізняється від візерунка з двома прорізами, розглянутого на занятті?

2. Порівняйте різні шаблони на екрані перегляду з d = 20Å і L = 100 нм для випущених електронів з довжинами хвиль 10Å, 100Å та 1000Å. Поясніть.

3. Показати, що зсув положення хвильового пакета на$x_{0}$ еквівалентний множенню k-простору подання на$\text{exp}[-ikx_{0}]$. Також показати, що зсув у представленні k-простору на$k_{0}$ еквівалентний множенню позиції хвильового пакета на$\text{exp}[-ik_{0}x]$. Покажіть, що подібні відносини тримають зрушення в часі і частоті.

4. Знайдіть$|F(\omega)|^{2}$, де$F(\omega)$ знаходиться перетворення Фур'є експоненціального розпаду:

$$F(\omega)= \mathcal{F}[e^{-at}u(t)] \nonumber$$

де u (t) - одинична функція кроку.

5. Покажіть, що якщо

$$(\Delta x)^{2} = \langle x^{2}\rangle - \langle x\rangle^{2} \nonumber$$

потім

$$\Delta x=\sigma \nonumber$$

де

$$\psi(x)=\text{exp}[-\frac{1}{4}\frac{(x-x_{0})^{2}}{\sigma^{2}}] \nonumber$$

6. Показати наступне:

(а)$\langle k\rangle=\frac{\langle A|k| A\rangle}{\langle A \mid A\rangle}=\frac{\left\langle\psi\left|-i \frac{d}{d x}\right| \psi\right\rangle}{\langle\psi \mid \psi\rangle}$

(б)$\langle \omega\rangle=\frac{\langle A|\omega| A\rangle}{\langle A \mid A\rangle}=\frac{\left\langle\psi\left|i \frac{d}{d t}\right| \psi\right\rangle}{\langle\psi \mid \psi\rangle}$

7. Вільна частинка обмежена для переміщення вздовж осі х. У момент t=0 хвильова функція задається

\ [\ PSI (x, t=0) =\ лівий\ {\ почати {масив} {cc}\ frac {1} {
\ sqrt {L}} e^ {i k_ {0} x} &\ frac {-L} {2}\ leq\ frac {L} {2}\\ 0 &\ text {інакше}\ кінець {масив}\ leq\ leq\ frac {L} {2}\\
0 &\ text {інакше}
\ кінець {масив}\ праворуч. \ номер\]

(а) Яке найбільш ймовірне значення імпульсу?

(b) Які найменш ймовірні значення імпульсу?

(c) Зробити приблизний ескіз хвильової функції в k -просторі, A (k, t = 0).

8. Комутатор двох операторів$\hat{A}$ і$\hat{B}$ визначається як

$$[\hat{A},\hat{B}]=\hat{A}\hat{B}-\hat{B}\hat{A} \nonumber$$

Оцініть наступні комутатори:

(а)$[\hat{x},\hat{x}^{2}]$

(б)$[\hat{p},\hat{p}^{2}]$

(c)$[\hat{x}^{2},\hat{p}^{2}]$

(г)$[\hat{x}\hat{p},\hat{p}\hat{x}]$

9. Розглянемо хвильову функцію

$$\psi(x)=\exp \left[-\frac{1}{2} \frac{x^{2}}{\sigma^{2}}(1+i C)\right] \nonumber$$

Покажіть, що

$$\left|\sigma_{x}\right|\left|\sigma_{k}\right| \geq \frac{1}{2} \sqrt{1+C^{2}} \nonumber$$

(Підказка: Покажіть, що$|\sigma_{k}^{2}|=\frac{\langle \psi|-\frac{d^{2}}{dx^{2}}|\psi \rangle}{\langle \psi|\psi \rangle}$

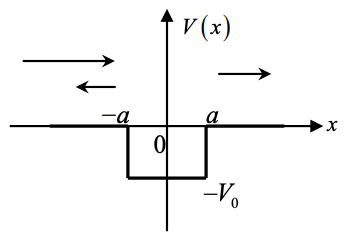
10. Для кінцевого квадрата, показаного нижче, обчисліть коефіцієнти відбиття та пропускання (E > 0).

Малюнок$\PageIndex{2}$: Кінцева потенційна яма.

11. Розглянемо електрон в наземному стані нескінченної квадратної ями шириною L. Яке значення очікування його швидкості? Яке очікуване значення його кінетичної енергії? Чи існує конфлікт між вашими результатами?

12. Вивести коефіцієнти відбиття і пропускання потенціалу$V(x)=A\delta(x)$, де A>0.

Малюнок$\PageIndex{3}$: Потенціал дельта-функції.

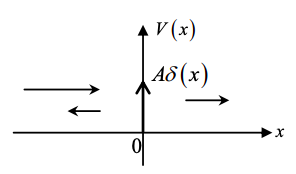
Одним із методів вирішення є прийняття рівняння Шредінгера з$V(x)=A\delta(x)$

$$-\frac{\hbar^{2}}{2 m} \frac{\partial^{2} \psi(x)}{\partial x^{2}}+A \delta(x) \psi(x)=E \psi(x) \nonumber$$

і інтеграції обох сторін від$-\epsilon$ до$\epsilon$ для$\epsilon$ дуже малого, щоб отримати обмеження

$$-\frac{\hbar^{2}}{2 m} \int_{-\varepsilon}^{+\varepsilon} \frac{\partial^{2} \psi(x)}{\partial x^{2}} d x+A \psi(0) \simeq 2 \varepsilon E \psi(0) \simeq 0 \nonumber$$

$\left.\Rightarrow \frac{d \psi}{d x}\right|_{x=\varepsilon}-\left.\frac{d \psi}{d x}\right|_{x=-\varepsilon}=\frac{2 m A}{\hbar^{2}} \psi(0)$

13. Розглянемо дві квантові ямки, кожна з яких має ширину w, розділену відстанню d.

Малюнок$\PageIndex{4}$: Будова квантових ямок.

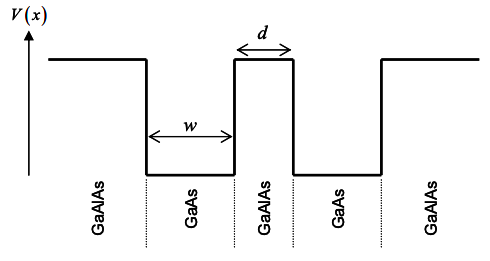
(а) З вашого розуміння хвильових функцій для частинки в коробці, побудуйте приблизну щільність ймовірності для кожного з двох найнижчих енергетичних режимів для цієї системи, коли дві квантові ямки ізольовані один від одного.

(б) Побудувати два найнижчі енергетичні режими, коли дві квантові ямки наближені один до одного таким чином, що d\ llw?

(c) Далі ми хочемо взяти тонкий шматочок іншого матеріалу і вставити його в структуру вище (де d\ llw), щоб вбити один з двох режимів частини (b), але залишити інший без впливу. Як би ви вибрали матеріал (в порівнянні з матеріалами, вже присутніми в структурі), і де повинен бути розміщений цей новий матеріал?