1.29: Кінцевий квадратний колодязь
- Page ID
- 32019
Коли обмежувальний потенціал кінцевий, ми вже не можемо вважати, що хвильова функція дорівнює нулю на кордоні свердловини. Для кінцевого обмежуючого потенціалу хвильова функція проникає в бар'єр: чим нижче обмежуючий потенціал, тим більше проникнення.
З Рівняння (1.27.1) загальним розв'язком хвильової функції всередині свердловини було
\[ \psi(x)=A\ cos(kx)+B\ sin(kx) , \nonumber \]
але з рішень для нескінченного колодязя ми бачимо, що всередині свердловини хвильова функція виглядає як
\[ \psi(x)=A\ cos(kx) \nonumber \]
або
\[ \psi(x)=A\ sin(kx) \nonumber \]
Спрощення можливе, оскільки потенціал свердловини симетричний навколо x = 0. Таким чином, щільність ймовірності також\(|ψ(x)|^{2}\) повинна бути симетричною,\(^{†}\) і дійсно обидва ψ (x) = sin (kx) і ψ (x) = cos (kx) мають симетричні розподіли ймовірностей, хоча ψ (x) = sin (kx) є антисиметричною хвильовою функцією.
Ми розглянемо симетричні (cos (kx)) та антисиметричні (sin (kx)) рішення хвилевих функцій окремо.
Симетрична хвильова функція
Можна припустити рішення форми:
\ [\ psi (x) =\ лівий\ {\ begin {масив} {ll}
e^ {\ альфа х} &\ текст {для} х\ LeQ-л/2\
A\ cos (k x) &\ текст {для} -L/2\ leq L/2\
e^ {-\ альфа х} &\ текст {для} х\ geq L/2\ eq {-\ альфа х}\ текст {для} х\ geq L/
\ end {масив}\ право. \ номер\]
де
\[ k = \sqrt{\frac{2mE}{\hbar^{2}}} \nonumber \]
і
\[ \alpha = \sqrt{\frac{2m(V_{0}-E)}{\hbar^{2}}} \nonumber \]
Зверніть увагу, що рішення, як написано, не нормалізується. Ми зможемо нормалізувати його пізніше.
Наступним кроком є оцінка константи А шляхом зіставлення кускових розчинів на краю свердловини. Нам потрібно враховувати тільки один край, тому що ми вже зафіксували симетрію розчину.
У правого краю, прирівнюючи амплітуду хвильової функції, дає
\[ \psi(L/2)=A\ cos(kL/2) = \text{exp}[-\alpha L/2] \nonumber \]
Прирівнювання нахилу хвильової функції дає
\[ \psi’(L/2)=-kA\ sin(kL/2) = -\alpha\ \text{exp}[-\alpha L/2] \nonumber \]
Рівняння ділення (1.29.8) на рівняння (1.29.7) для усунення A дає
\[ tan(kL/2)=\alpha /k \nonumber \]
Але\(\alpha\) і k - обидві функції енергії
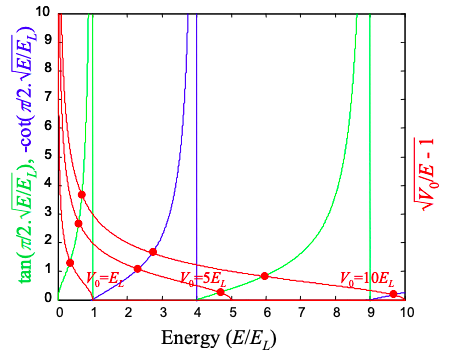
\[ tan(\frac{\pi}{2}\sqrt{\frac{E}{E_{L}}}) = \sqrt{\frac{V_{0}-E}{E}} \nonumber \]
де ми визначили нескінченний квадратний колодязь заземлений стан енергії
\[ E_{L}=\frac{\hbar^{2}\pi^{2}}{2mL^{2}} \nonumber \]
Як і в випадку нескінченного квадратного колодязя, ми знаходимо, що тільки певні, дискретні, значення енергії дають рішення. Ще раз квантуються енергії електронних станів в лунці. Для отримання енергій нам потрібно розв'язати Рівняння (1.29.10). На жаль, це трансцендентне рівняння, яке має вирішуватися чисельно або графічно. Побудовуємо розв'язки на малюнку 1.29.1.
Антисиметрична хвильова функція
Антисиметричні розв'язки знаходять аналогічно симетричним розв'язкам. Спочатку припустимо антисиметричне рішення виду:
\ [\ psi (x) =\ лівий\ {\ begin {масив} {ll}
e^ {\ альфа х} &\ текст {для} х\ LeQ-l/2\
A\ sin (k x) &\ текст {для} -L/2\ leq L/2\\
-e^ {-\ альфа х} &\ текст {для} х\ geq L/2
\ end {масив}\ право. \ номер\]
Потім оцінюємо константу А шляхом зіставлення кускових розчинів на краю свердловини. Знову ж таки, нам потрібно розглянути тільки один край, тому що ми вже зафіксували симетрію розчину.
У правого краю, прирівнюючи амплітуду хвильової функції, дає
\[ \psi(L/2)=A\ sin(kL/2)=-\text{exp}[-\alpha L/2] \nonumber \]
Прирівнювання нахилу хвильової функції дає
\[ \psi’(L/2)=kA\ cos(kL/2)=\alpha\ \text{exp}[-\alpha L/2] \nonumber \]
Рівняння ділення (1.29.8) на рівняння (1.29.7) для усунення A дає
\[ cot(kL/2)=-\alpha /k \nonumber \]
Розширення\(\alpha\) і k в плані енергії
\[ -cot(\frac{\pi}{2}\sqrt{\frac{E}{E_{L}}}) = \sqrt{\frac{V_{0}-E}{E}} . \nonumber \]
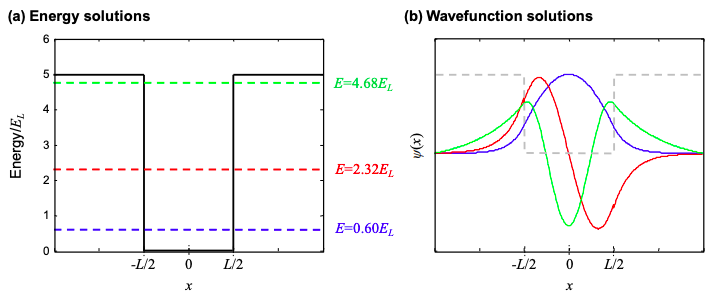
На малюнку 1.29.1 вирішуємо для енергії. Зверніть увагу, що завжди є хоча б один пов'язаний розчин незалежно від того, наскільки неглибокий колодязь. На малюнку 1.29.2 ми будуємо розв'язки для обмежуючого потенціалу\(V_{0}=5.E_{L}\).