6.16: Цифрові приймачі зв'язку

Цілі навчання

• Бітові потоки через цифрові приймачі зв'язку.

Приймач, зацікавлений у переданому бітовому потоці, повинен виконувати два завдання, коли$r(t)$ починається отримана форма сигналу.

• Він повинен визначити, коли відбуваються бітові межі: приймач повинен синхронізуватися з переданим сигналом. Оскільки передавач і приймач розроблені узгоджено, обидва використовують однакове значення для бітового інтервалу$T$. Синхронізація може відбуватися через те, що передавач починає відправку з еталонної бітової послідовності, відомої як преамбула. Ця послідовність еталонних бітів зазвичай є чергуваною послідовністю, як показано у прикладі квадратної хвилі та у прикладі FSK. Приймач знає, що таке послідовність бітів преамбула і використовує її для визначення, коли відбуваються межі бітів. Ця процедура дорівнює тому, що в цифровому обладнанні, як сигналізація самосинхронізації: Приймач бітового потоку повинен виводити годинник - коли відбуваються межі бітів - зі свого вхідного сигналу. Оскільки приймач зазвичай не визначає, який біт був відправлений, поки не відбудеться синхронізація, він не знає, коли під час преамбули він отримав синхронізацію. Передавач сигналізує про кінець преамбули шляхом перемикання на другу бітову послідовність. Друга фаза преамбули інформує приймача, що біти даних ось-ось прийдуть і що преамбула майже закінчена.
• Після синхронізації та передачі бітів даних приймач повинен кожні$T$ секунди визначити, який біт був переданий протягом попереднього бітового інтервалу. Ми зосереджуємося на цьому аспекті цифрового приймача, оскільки ця стратегія також використовується при синхронізації.

Приймач для цифрового зв'язку відомий як узгоджений фільтр.

Рисунок 6.16.1 Оптимальною структурою приймача для цифрового зв'язку, що стикається з адитивними каналами білого шуму, є зображений узгоджений фільтр

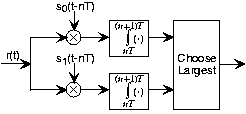
Цей приймач, показаний на малюнку 6.16.1, множить прийнятий сигнал на кожен з можливих членів набору сигналу передавача, інтегрує продукт через бітовий інтервал та порівнює результати. Який би шлях через приймач дає найбільше значення відповідає рішенню приймача щодо того, який біт був відправлений протягом попереднього бітового інтервалу. Для наступного бітового інтервалу множення та інтеграція починається знову, а наступне бітове рішення приймається в кінці бітового інтервалу. Математично отримане значення$b(n)$ задається:

$$b(n)=\hat{b}(n)=\underset{i}{\arg max}\int_{nT}^{(n+1)T}r(t)s_{i}(t)dt \nonumber$$

Можливо, ви не бачили

$$\underset{i}{\arg max} \nonumber$$

позначення перед.

$$\max _{i}\left \{ i, \cdot \right \} \nonumber$$

виводить максимальне значення свого аргументу щодо індексу$i$

$$\underset{i}{\arg max} \nonumber$$

дорівнює значенню індексу, який дає максимум. Зверніть увагу, що точне числове значення виходу інтегратора не має значення; значення має його значення щодо виходу іншого інтегратора.

Припустимо ідеальний канал на даний момент: Прийнятий сигнал дорівнює переданому. Якби біт 0 був відправлений за допомогою набору сигналу BPSK базової смуги, виходи інтегратора були б

$$\int_{nT}^{(n+1)T}r(t)s_{0}(t)dt=A^{2}T \nonumber$$

$$\int_{nT}^{(n+1)T}r(t)s_{1}(t)dt=-(A^{2}T) \nonumber$$

Якщо біт 1 був відправлений,

$$\int_{nT}^{(n+1)T}r(t)s_{0}(t)dt=-(A^{2}T) \nonumber$$

$$\int_{nT}^{(n+1)T}r(t)s_{1}(t)dt=A^{2}T \nonumber$$

Вправа$\PageIndex{1}$

Чи можете ви розробити приймач для наборів сигналів BPSK, який вимагає лише однієї комбінації мультиплікатор-інтегратор?

Рішення

У BPSK сигнали є негативами один одного:

$$s_{1}(t)=-s_{0}(t) \nonumber$$

Отже, вихід кожної комбінації множник-інтегратор є негативом іншого. Тому вибір найбільшого означає вибір, який з них є позитивним. Нам потрібно лише обчислити один з них. Якщо це позитивно, ми закінчили. Якщо він негативний, вибираємо інший сигнал.

Вправа$\PageIndex{1}$

Який відповідний результат при використанні амплітудно-модульованого набору сигналу BPSK?

Рішення

Відповідні виходи фільтра

$$\pm \left ( \frac{A^{2}T}{2} \right ) \nonumber$$

тому що синусоїда має меншу потужність, ніж імпульс, що має однакову амплітуду.

Зрозуміло, що цей приймач завжди вибирав би біт правильно. Затухання каналу не вплине на цю коректність; це лише зменшить значення, але все, що має значення, є найбільшим.