6.3: Провідні канали

Цілі навчання

• Проведено аналіз і передавальні характеристики дротових каналів.

Провідні канали були першими використані для електричних комунікацій в середині дев'ятнадцятого століття для телеграфу. Тут канал являє собою один з декількох проводів, що з'єднують передавач з приймачем. Передавач просто створює напругу, пов'язану з сигналом повідомлення, і застосовує його до проводів (ів). Ми повинні мати ланцюг - замкнутий шлях, який підтримує потік струму. У випадку з однопровідними комунікаціями в якості зворотного шляху струму використовується земля. По суті, термін заземлення для опорного вузла в схемах зародився в однодротових телеграфах. Ви можете собі уявити, що електричні характеристики землі сильно мінливі, і вони є. Однопровідні металеві канали не можуть підтримувати високоякісну передачу сигналу, що має пропускну здатність понад кілька сотень герц на будь-якій помітній відстані.

Малюнок 6.3.1 Коаксіальний кабель складається з одного провідника, обмотаного навколо центрального провідника. Цей тип кабелю підтримує більш широкі сигнали пропускної здатності, ніж кручена пара, і знаходить застосування в кабельному телебаченні та Ethernet.

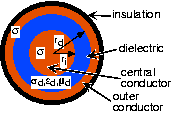
Отже, більшість провідних каналів сьогодні по суті складаються з пар провідних проводів (рис. 6.3.1), а передавач подає напругу, пов'язану з повідомленням, по парі. Те, як ці пари проводів фізично налаштовані, сильно впливає на їх характеристики передачі. Одним із прикладів є кручена пара, де дроти обмотані один про одного. Телефонні кабелі - один із прикладів каналу кручений пари. Інший - коаксіальний кабель, де концентричний провідник оточує центральний провід з діелектричним матеріалом між ними. Коаксіальний кабель, який інженери люб'язно називають «коаксіальним», - це те, що Ethernet використовує як свій канал. У будь-якому випадку провідні канали утворюють спеціальну схему між передавачем і приймачем. Як ми виявимо згодом, кілька передач можуть ділитися схемою за допомогою методів амплітудної модуляції; комерційне кабельне телебачення є прикладом. Ці інформаційно-несучі схеми сконструйовані таким чином, що перешкоди від довколишніх електромагнітних джерел зведені до мінімуму. Таким чином, до часу сигнали надходять на приймач, вони відносно безперешкодно- і безшумні.

Як кручена пара, так і коаксіальний є прикладами ліній електропередачі, які мають модель схеми, показану на малюнку, для нескінченно невеликої довжини. Ця модель схеми виникає внаслідок розв'язання рівнянь Максвелла для конкретної геометрії лінії електропередачі.

Малюнок 6.3.2 Так звана модель розподілених параметрів для двожильних кабелів має зображену структуру моделі схеми. Значення елементів залежать від геометрії та властивостей матеріалів, використовуваних для побудови лінії електропередачі.

Послідовний опір виходить від провідника, використовуваного в проводах, і від геометрії провідника. Індуктивність і ємність походять від геометрії лінії електропередачі, а паралельна провідність від середовища між дротяною парою. Зауважте, що всі елементи схеми мають значення, виражені добутком постійної довжини; це позначення означає, що значення елементів тут мають одиниці одиниці довжини. Наприклад, послідовний опір\[\widetilde{R} \nonumber \] має одиниці Ом/метр. Для коаксіального кабелю значення елементів залежать від радіуса внутрішнього провідника r _i, зовнішнього радіуса діелектрика r _d, провідності провідників σ, а провідності σ _d, діелектричної проникності ε _d, і магнітна проникність μ _d діелектрика як

\[\widetilde{R}=\frac{1}{2\pi \delta \sigma }\left ( \frac{1}{r_{d}}+ \frac{1}{r_{i}}\right ) \nonumber \]

\[\widetilde{C}=\frac{2\pi \varepsilon _{d}}{\ln \left ( \frac{r_{d}}{r_{i}} \right )} \nonumber \]

\[\widetilde{G}=\frac{2(\pi ,\sigma _{d})}{\ln \left ( \frac{r_{d}}{r_{i}} \right )} \nonumber \]

\[\widetilde{L}=\frac{\mu _{d}}{2\pi }\ln \left ( \frac{r_{d}}{r_{i}} \right ) \nonumber \]

Для кручений пари, що має поділ d між провідниками, що мають провідність σ і загальний радіус r і занурені в середовище, що має діелектричні і магнітні властивості, значення елементів потім

\[\widetilde{R}=\frac{1}{\pi r\delta \sigma } \nonumber \]

\[\widetilde{C}=\frac{\pi \varepsilon }{\arccos h\left ( \frac{d}{2r} \right )} \nonumber \]

\[\widetilde{G}=\frac{\pi \sigma }{\arccos h\left ( \frac{d}{2r} \right )} \nonumber \]

\[\widetilde{L}=\frac{\mu }{\pi }\left ( \frac{d}{2r}+\arccos h\left( \frac{d}{2r}\right )\right ) \nonumber \]

Напруга між двома провідниками і струм, що протікає через них, буде залежати від відстані x по лінії електропередачі, а також від часу. Висловлюємо цю залежність як v (x, t) і i (x, t). Коли ми розміщуємо синусоїдальне джерело на одному кінці лінії електропередачі, ці напруги та струми також будуть синусоїдальними, оскільки модель лінії електропередачі складається з елементів лінійної схеми. Як це прийнято при аналізі лінійних ланцюгів, ми виражаємо напруги та струми як реальну частину складних експоненціальних сигналів, а змінні схеми записуємо як складну амплітуду - тут залежну від відстані - разів складну експоненціальну:

\[v(x,t)=\Re \left ( V(x)e^{i2\pi ft} \right ) \nonumber \]

\[i(x,t)=\Re \left ( I(x)e^{i2\pi ft} \right ) \nonumber \]

Використовуючи модель схеми лінії електропередачі, ми знаходимо з KCL, KVL та v-i співвідношення рівнянь, що керують комплексними амплітудами.

KCL і центральний вузол

\[I(x)=I(x-\Delta (x))-V(x)(\widetilde{G}+i2\pi f\widetilde{C})\Delta (x) \nonumber \]

V-I відношення для серії RL

\[V(x)-V(x+\Delta (x))=I(x)(\widetilde{R}+i2\pi f\widetilde{L})\Delta (x) \nonumber \]

Перестановка та прийняття межі Δ (x) →0 дає так звані рівняння лінії електропередачі.

\[\frac{\mathrm{d} }{\mathrm{d} x}I(x)=-\left ( (\widetilde{G}+i2\pi f\widetilde{C})V(x) \right ) \nonumber \]

\[\frac{\mathrm{d} }{\mathrm{d} x}V(x)=-\left ( (\widetilde{R}+i2\pi f\widetilde{L})I(x) \right ) \nonumber \]

Об'єднавши ці рівняння, ми можемо отримати єдине рівняння, яке регулює, як змінюється амплітуда напруги або комплексної амплітуди струму з положенням вздовж лінії електропередачі. Взяття похідної другого рівняння і включення першого рівняння в результат дає рівняння, що керує напругою.

\[\frac{\mathrm{d}^{2} }{\mathrm{d} x^{2}}V(x)= (\widetilde{G}+i2\pi f\widetilde{C})(\widetilde{R}+i2\pi f\widetilde{L})V(x) \nonumber \]

Рішення цього рівняння

\[V(x)=V_{+}e^{-(\gamma x)}+V_{-}e^{\gamma x} \nonumber \]

Обчислення його другої похідної і порівняння результату з нашим рівнянням по напрузі дозволяє перевірити це рішення.

\[\frac{\mathrm{d} ^{2}}{\mathrm{d} x^{2}}V(x)=\gamma ^{2}\left ( V_{+}e^{-(\gamma x)}+V_{-}e^{\gamma x}\right ) \nonumber \]

\[\therefore \frac{\mathrm{d} ^{2}}{\mathrm{d} x^{2}}V(x)=\gamma ^{2}V(x) \nonumber \]

Наше рішення працює до тих пір, поки кількість γ задовольняє

\[\gamma =\pm \left ( \sqrt{(\widetilde{G}+i2\pi f\widetilde{C})(\widetilde{R}+i2\pi f\widetilde{L})} \right ) \nonumber \]

\[\therefore \gamma =\pm (a(f)+ib(f)) \nonumber \]

Таким чином, γ залежить від частоти, і ми виражаємо її в терміні реальної та уявної частин, як зазначено. Величини V ₊ і V _- це константи, що визначаються джерелом і фізичними міркуваннями. Наприклад, нехай просторове походження буде серединою моделі лінії електропередачі на малюнку 6.3.2. Оскільки модель схеми містить прості елементи схеми, фізично можливі рішення для амплітуди напруги не можуть збільшуватися з відстанню вздовж лінії електропередачі. Висловлення γ у терміні його реальної та уявної частин у нашому розв'язанні показує, що такі збільшення є (математичною) можливістю.

\[V(x)=V_{+}e^{(-(a+ib))x}+V_{-}e^{(a+ib)x} \nonumber \]

Напруга не може збільшуватися без обмеження; оскільки a (f) завжди позитивний, ми повинні розділити рішення для негативного та позитивного x. Перший член збільшуватиметься експоненціально для x<0, якщо V ₊ =0 у цій області; аналогічний результат застосовується до V _- для x>0. Ці фізичні обмеження дають нам більш чисте рішення.

\[V(x)=\begin{cases} V_{+}e^{(-(a+ib))x} & \text{ if } x> 0 \\ V_{-}e^{(a+ib)x} & \text{ if } x< 0 \end{cases} \nonumber \]

Це рішення говорить про те, що напруги (і струми теж) зменшуватимуться експоненціально вздовж лінії електропередачі. Просторова константа, також відома як постійна загасання, - це відстань, на якій напруга зменшується в рази 1/e. Він дорівнює зворотному a (f), що залежить від частоти, і виражається виробниками в одиницях дБ/м.

Наявність уявної частини γ, b (f) також дає уявлення про те, як працюють лінії електропередачі. Оскільки рішення для x> 0 пропорційно e ^{- (ibx)}, ми знаємо, що комплексна амплітуда напруги буде змінюватися синусоїдально в просторі. Комплексне рішення по напрузі має вигляд

\[v(x,t)=\Re \left ( V_{+}e^{-(ax)}e^{i(2\pi ft-bx)} \right ) \nonumber \]

Складна експоненціальна ділянка має вигляд поширюється хвилі. Якби ми могли зробити знімок напруги (сфотографуйте його на t = t ₁), ми побачили б синусоїдальну форму хвилі вздовж лінії електропередачі. Один період цієї варіації, відомий як довжина хвилі, дорівнює

\[\lambda =\frac{2\pi }{b} \nonumber \]

Якби ми зробили другий знімок пізніше t = t _2, ми також побачили б синусоїдальну напругу.

Тому що

\[2\pi ft_{2}-bx=2\pi f(t_{1}+t_{2}-t_{1})-bx=2\pi ft_{1}-b\left ( x-\frac{2\pi f}{b} (t_{2}-t_{1})\right ) \nonumber \]

друга форма хвилі здається першою, але затриманою - зміщеною вправо - у просторі. Таким чином, з'явилася напруга рухатися вправо зі швидкістю, рівною

\[\frac{2\pi f}{b}\; where \; b> 0 \nonumber \]

Позначимо цю швидкість поширення c, і вона дорівнює

\[c-=\left | \frac{2\pi f}{\Im \left ( \sqrt{(\widetilde{G}+i2\pi f\widetilde{C})(\widetilde{R}+i2\pi f\widetilde{L})} \right )} \right | \nonumber \]

У високочастотній області, де

\[i2\pi f\widetilde{L}\geqslant \widetilde{R} \; and\; i2\pi f\widetilde{C}\geqslant \widetilde{G} \nonumber \]

кількість під радикалом спрощує

\[-4\left ( \pi ^{2} ,f^{2},\widetilde{L},\widetilde{C}\right ) \nonumber \]

і ми знаходимо швидкість поширення, щоб бути

\[\lim_{f\rightarrow \infty }c=\frac{1}{\sqrt{\widetilde{L}\widetilde{C}}} \nonumber \]

Для типового коаксіального кабелю ця швидкість поширення становить частку (від однієї третини до двох третин) швидкості світла.

Вправа\(\PageIndex{1}\)

Знайдіть швидкість поширення з точки зору фізичних параметрів як для прикладів коаксіального кабелю, так і для крученої пари.

Рішення

В обох випадках відповідь залежить менше від геометрії, ніж від властивостей матеріалу. Для коаксіального кабелю,

\[c=\frac{1}{\sqrt{\mu _{d}\varepsilon _{d}}} \nonumber \]

Для кручений пари,

\[c=\frac{1}{\sqrt{\mu \varepsilon }}\sqrt{\frac{\arccos h\left ( \frac{d}{2r} \right )}{\frac{\delta }{2r}+\arccos h\left ( \frac{d}{2r}\right )}} \nonumber \]

Використовуючи друге рівняння лінії електропередачі зверху, ми можемо вирішити для комплексної амплітуди струму. Розглядаючи просторову область x>0, наприклад, ми виявимо, що

\[\frac{\mathrm{d} }{\mathrm{d} x}V(x)=-(\gamma V(x))=\left ( -(\widetilde{R}+i2\pi f\widetilde{L})I(x) \right ) \nonumber \]

а значить, співвідношення амплітуд комплексу напруги і струму не залежить від відстані.

\[\frac{V(x)}{I(x)}=\sqrt{\frac{\widetilde{R}+i2\pi f\widetilde{L}}{\widetilde{G}+i2\pi f\widetilde{C}}} \nonumber \]

\[\frac{V(x)}{I(x)}=Z_{0} \nonumber \]

Кількість Z ₀ відома як характеристичний імпеданс лінії електропередачі. Зверніть увагу, що коли частота сигналу досить висока, характеристичний опір є реальним, а це означає, що лінія передачі виглядає резистивною в цьому високочастотному режимі.

\[\lim_{f\rightarrow \infty }Z_{0}=\sqrt{\frac{\widetilde{L}}{\widetilde{C}}} \nonumber \]

Типові значення для характеристичного імпедансу - 50 і 75 Ом.

Пов'язаною лінією електропередачі є оптичне волокно. Тут електромагнітне поле - світло, і воно поширюється вниз по циліндру зі скла. У цій ситуації у нас немає двох провідників - насправді у нас немає - і енергія поширюється в тому, що відповідає діелектричному матеріалу коаксіального кабелю. Волоконно-оптичний зв'язок має точно такі ж властивості, як і інші лінії електропередачі: Сила сигналу зменшується експоненціально відповідно до космічної константи волокна і поширюється з деякою швидкістю менше, ніж світло буде у вільному просторі. З охоплюючого погляду рівнянь Максвелла єдиною відмінністю є частота електромагнітного сигналу. Оскільки електричних провідників немає, а волокно захищене непрозорим «ізолятором», передача оптичного волокна не перешкоджає.

Вправа\(\PageIndex{1}\)

З таблиць фізичних констант знайдіть частоту синусоїди посередині видимого світлового діапазону. Порівняйте цю частоту з частотою сигналу кабельного телебачення середньої частоти.

Рішення

Ви можете знайти ці частоти на діаграмі розподілу спектра. Світло в середині видимої смуги має довжину хвилі близько 600 нм, що відповідає частоті 5 × 10 ¹⁴ Гц. Кабельне телебачення передає в тій же смузі частот, що і мовлення телебачення (близько 200 МГц або 2 × 10 ⁸ Гц). Таким чином, видимі електромагнітні частоти на шість порядків вище!

Підводячи підсумок, ми використовуємо лінії електропередачі для високочастотного дротового сигналу зв'язку. У провідному зв'язку ми маємо пряме фізичне з'єднання - ланцюг - між передавачем і приймачем. Коли ми вибираємо характеристики лінії електропередачі та частоту передачі, щоб ми працювали у високочастотному режимі, сигнали не фільтруються, оскільки вони поширюються вздовж лінії електропередачі: Характеристичний опір є реальним значенням - еквівалентний імпеданс лінії електропередачі є резистором - і всі компоненти сигналу на різних частотах поширюються з однаковою швидкістю. Амплітуда переданого сигналу зменшується експоненціально вздовж лінії електропередачі. Відзначимо, що в високочастотному режимі константа простору дорівнює приблизно нулю, а значить загасання досить мало.

Вправа\(\PageIndex{1}\)

Яке граничне значення космічної константи в високочастотному режимі?

Рішення

Зі збільшенням частоти

\[2\pi f\widetilde{C}\geqslant \widetilde{G}\; and \; 2\pi f\widetilde{L}\geqslant \widetilde{R} \nonumber \]

У цій високочастотній області,

\[\gamma =i2\pi f\sqrt{\widetilde{L}\widetilde{C}}\sqrt{\left ( 1+\frac{\widetilde{G}}{i2\pi f\widetilde{C}} \right )\left ( 1+\frac{\widetilde{R}}{i2\pi f\widetilde{L}} \right )} \nonumber \]

\[\gamma \simeq i2\pi f\sqrt{\widetilde{L}\widetilde{C}}\times \left ( 1+\frac{1}{2}\frac{1}{i2\pi \pi f} \left ( \frac{\widetilde{G}}{\widetilde{C}} +\frac{\widetilde{R}}{\widetilde{L}}\right )\right ) \nonumber \]

\[\gamma \simeq i2\pi f\sqrt{\widetilde{L}\widetilde{C}}+\frac{1}{2} \left ( \widetilde{G}\sqrt{\frac{\widetilde{L}}{\widetilde{C}} }+\widetilde{R}\sqrt{\frac{\widetilde{C}}{\widetilde{L}}}\right ) \nonumber \]

Таким чином, константа загасання (пробіл) дорівнює дійсній частині цього виразу, і дорівнює

\[a(f)=\frac{\widetilde{G}Z_{0}+\frac{\widetilde{R}}{Z_{0}}}{2} \nonumber \]