5.10: Спектрограми

Last updated
Save as PDF

Page ID: 32940

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Спектрограми візуально представляють мовний сигнал, а розрахунок спектрограми коротко пояснюється.

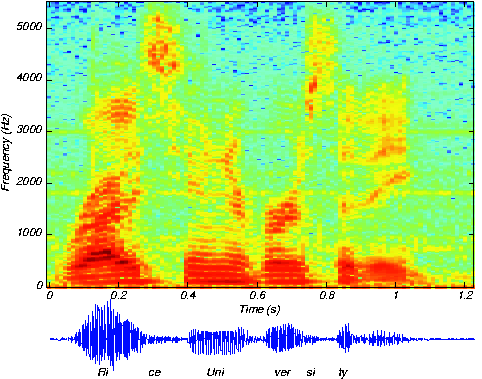
Ми знаємо, як придбати аналогові сигнали для цифрової обробки (попередня фільтрація, вибірка та A/D перетворення) та обчислити спектри дискретних сигналів часу (за допомогою алгоритму БПФ), давайте поставимо ці різні компоненти разом, щоб дізнатися, як розраховується спектрограма, показана на малюнку 5.10.1 нижче, яка використовується для аналізу мови. Мова відбиралася зі швидкістю 11,025 кГц і проходила через 16-бітний A/D перетворювач.

Приклад\(\PageIndex{1}\):

Музичні компакт-диски (компакт-диски) кодують свої сигнали з частотою дискретизації 44,1 кГц. Ми дізнаємося обґрунтування цього числа пізніше. Частота дискретизації 11.025 кГц для мови становить 1/4 частоти дискретизації CD і була найнижчою доступною частотою дискретизації, порівнянною з пропускною здатністю мовного сигналу, доступною на моєму комп'ютері.

Вправа\(\PageIndex{1}\)

Дивлячись на малюнок 5.10.1, сигнал тривав трохи більше 1,2 секунди. Як довго був вибірковий сигнал (з точки зору зразків)? Яким був datarate під час процесу вибірки в біт/с (біти в секунду)? Якщо припустити, що зберігання комп'ютера організовано з точки зору байтів (8-бітових величин), скільки байт пам'яті комп'ютера споживає мова?

Малюнок 5.10.1 S *пектрограма для аналізу* *мови*

Рішення

Кількість зразків дорівнює 1,2 × 11025 = 13230

Швидкість передачі даних становить 11025 × 16 = 176,4 кбіт/с

Необхідне сховище становило б 26460 байт

Отриманий дискретно-часовий сигнал, показаний внизу малюнка 5.10.1, чітко змінює свій характер з часом. Для відображення цих спектральних змін довгий сигнал був розділений на кадри: порівняно короткі, суміжні групи зразків. Концептуально перетворення Фур'є кожного кадру обчислюється за допомогою БПФ. Кожен кадр не настільки довгий, щоб значні зміни сигналу зберігалися всередині кадру, але не настільки короткий, щоб ми втратили спектральний характер сигналу. Грубо кажучи, спектр мовного сигналу оцінюється на послідовних часових відрізках і укладається пліч-о-пліч так, що вісь x відповідає часу та частоті осі y, з кольором, що вказує спектральну амплітуду.

Важлива деталь з'являється, коли ми розглядаємо кожен обрамлений сигнал з наведеного вище малюнка.

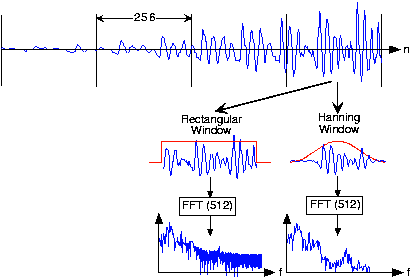
Малюнок 5.10.1 передбачав створення кадрів, тут відмічених вертикальними лініями, які були 256 зразків довжиною і знаходження спектра кожного. Якщо застосовується прямокутне вікно (відповідне вилучення кадру з сигналу), в спектрі (середина нижнього ряду) з'являються коливання. Застосування вікна Ханнінга витончено звужує сигнал до країв кадру, тим самим даючи більш точний розрахунок спектру сигналу в той момент часу.

По краях кадру сигнал може змінюватися дуже різко, особливість відсутня в вихідному сигналі. Перетворення такого відрізка виявляє цікаве коливання в спектрі, артефакт, безпосередньо пов'язаний з цим різким зміною амплітуди. Кращим способом кадру сигналів для спектрограм є застосування вікна: Сформуйте значення сигналу всередині кадру так, щоб сигнал граціозно затухав, коли він наближається до країв. Це формування здійснюється множенням обрамленого сигналу на послідовність w (n). При розділенні сигналу ми по суті застосували прямокутне вікно:

\[w(n)=1,0\leq n\leq N-1 \nonumber \]

Набагато більш витонченим вікном є вікно Ханнінга; воно має форму косинуса

\[w(n)=\frac{1}{2}\left ( 1-\cos \left ( \frac{2\pi n}{N}\right )\right ) \nonumber \]

Як показано на малюнку 5.10.2, це формування значно зменшує помилкові коливання в спектрі кожного кадру. Розглядаючи спектр віконної рами Ханнінга, ми виявимо, що коливання, що виникають в результаті застосування прямокутного вікна, затьмарювали формант (той, що розташований трохи більше половини частоти Найквіста).

Вправа\(\PageIndex{1}\)

Що може бути джерелом цих коливань? Щоб отримати деяке розуміння, яка довжина- 2N дискретне перетворення Фур'є довжини- N імпульсу? Імпульс емулює прямокутне вікно, і неодмінно має ребра. Порівняйте свою відповідь з перетворенням довжини- 2N довжини- N вікна Ханнінга.

Рішення

Коливання обумовлені перетворенням Фур'є вікна вагона, яке дорівнює функції sinc.

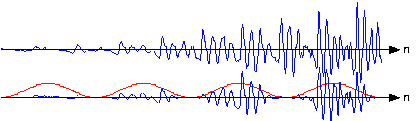
Малюнок 5.10.3 У порівнянні з вихідним мовним сегментом, показаним у верхньому сюжеті, що не перекривається віконний варіант Ханнінга, показаний нижче, дуже рваний. Зрозуміло, що спектральна інформація, витягнута з нижньої ділянки, цілком може пропустити важливі функції, присутні в оригіналі.

Якщо послідовно вивчити віконні розділи сигналу, щоб вивчити вплив вікна на амплітуду сигналу, ми побачимо, що нам вдалося амплітудно-модулювати сигнал з періодично повторюваним вікном (рис. 5.10.3). Щоб полегшити цю проблему, кадри перекриваються (як правило, на половину тривалості кадру). Це рішення вимагає більше розрахунків перетворення Фур'є, ніж потрібно для прямокутного віконного вікна, але спектри набагато краще поводяться і спектральні зміни набагато краще фіксуються.

Мовний сигнал, як показано на малюнку 5.10.1 вище, розділяється на перекриваються рамки однакової довжини, з вікном Ханнінга, застосованим до кожного кадру. Спектри кожного з них розраховуються і відображаються в спектрограмах з частотою, що розширюється по вертикалі, розташуванням часу вікна, що працює горизонтально, і спектральною величиною кольоровим кодуванням. Малюнок 5.10.4 ілюструє ці обчислення.

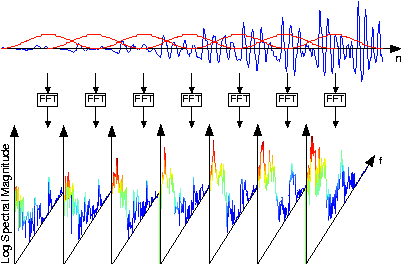
Малюнок 5.10.4 Вихідний мовний відрізок і застосована до нього послідовність перекриття вікон Ханнінга показані у верхній частині. Кадри були 256 зразків довжиною і вікно Ханнінга було застосовано з напіврамковим перекриттям. Була обчислена довжина 512 БПФ кожного кадру, причому величина перших 257 значень БПФ відображається вертикально, зі значеннями спектральної амплітуди, кодованими кольором.

Вправа\(\PageIndex{1}\)

Чому конкретні значення 256 для N і 512 для K? Інша проблема полягає в тому, як обчислювалося перетворення довжини-512 кожного віконного кадру довжини-256?

Рішення

Ці числа є потужностями двох, і алгоритм БПФ може бути використаний з цими довжинами. Щоб обчислити більш тривале перетворення, ніж тривалість вхідного сигналу, ми просто нульову панель сигналу.