5.4: Квантування амплітуди

Last updated
Save as PDF

Page ID: 32868

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Аналого-цифрове перетворення.

Теорема вибірки говорить, що якщо ми досить швидко відбираємо обмежений діапазон сигналу s (t), його можна відновити без помилок з його зразків

\[s(nT_{s}),n\in \left \{ ...,-1,0,1,... \right \} \nonumber \]

Вибірка - це лише перша фаза збору даних у комп'ютер: Обчислювальна обробка додатково вимагає квантування зразків: аналогові значення перетворюються в цифрову форму. Коротше кажучи, ми виконали аналого-цифрове (A/D) перетворення.

Рисунок 5.4.1 Трибітний A/D перетворювач призначає напругу в діапазоні **[-1,1]** одному з восьми цілих чисел від 0 до 7. Наприклад, всім входам, що мають значення, що лежать від 0,5 до 0,75, присвоюється ціле значення шість і, після перетворення назад в аналогове значення, всі вони стають 0,625. Ширина одного інтервалу квантування Δ дорівнює **2/2 ^B**. На нижній панелі відображається сигнал, що проходить через аналого-цифровий перетворювач, де B - кількість бітів, використовуваних в процесі A/D перетворення (3 у випадку, зображеному тут). Спочатку він вибірковий, потім амплітудно-квантується до трьох біт. Зверніть увагу, як вибіркова форма сигналу спотворюється після квантування амплітуди. Наприклад, два значення сигналу між 0,5 і 0,75 стають 0,625. Це спотворення є незворотним; його можна зменшити (але не усунути), використовуючи більше бітів в A/D перетворювачі.

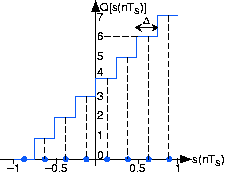
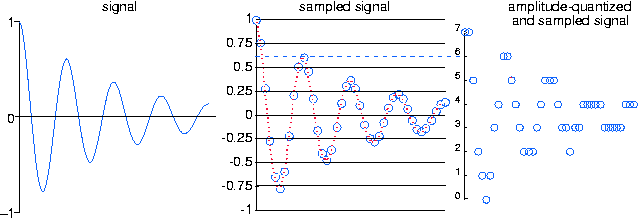
Явище, що нагадує помилки, що виникають при представленні чисел на комп'ютері, запобігає перетворенню амплітуди сигналу без помилок у подання двійкового числа. При аналого-цифровому перетворенні передбачається, що сигнал лежить в заданому діапазоні. Припускаючи, що ми можемо масштабувати сигнал, не впливаючи на інформацію, яку він висловлює, ми визначимо цей діапазон як [-1,1]. Крім того, A/D перетворювач призначає амплітудні значення в цьому діапазоні набору цілих чисел. B-бітовий перетворювач створює одне з цілих чисел

\[\left \{0,1,...,2^{B} -1\right \} \nonumber \]

для кожного вибіркового входу. На малюнку 5.4.1 показано, як трибітний A/D перетворювач призначає вхідні значення цілим числам. Визначаємо інтервал квантування, який буде діапазоном значень, присвоєних одному і тому ж цілому числу. Таким чином, для нашого прикладу трибітного A/D перетворювача інтервал квантування Δ дорівнює 0,25; в загальному - 2/2 ^В.

Вправа\(\PageIndex{1}\)

Згадуючи сюжет середньодобових максимумів у цій проблемі частотної області, чому ця ділянка настільки зубчаста? Інтерпретуйте цей ефект з точки зору аналого-цифрового перетворення.

Рішення

Побудовані температури були квантовані до найближчого ступеня. Таким чином, амплітуда високої температури квантувалася як форма A/D перетворення.

Оскільки значення, що лежать в будь-якому місці в інтервалі квантування, присвоюються однакові значення для комп'ютерної обробки, вихідне значення амплітуди не може бути відновлено без помилок. Як правило, D/A перетворювач, пристрій, який перетворює цілі числа в амплітуди, призначає амплітуду, рівну значенню, що лежить на півдорозі в інтервалі квантування. Ціле число 6 буде присвоєно амплітуді 0.625 в цій схемі. Помилка, введена перетворенням сигналу з аналогового в цифрову форму шляхом вибірки та квантування амплітуди, потім знову буде половиною інтервалу квантування для кожного значення амплітуди. Таким чином, так звана A/D похибка дорівнює половині ширини інтервалу квантування: 1/2 ^B. Оскільки ми виправили діапазон вхідної амплітуди, чим більше бітів доступні в A/D перетворювачі, тим менша помилка квантування.

Щоб глибше проаналізувати помилку квантування амплітуди, нам потрібно обчислити відношення сигнал/шум, яке дорівнює відношенню потужності сигналу та потужності похибки квантування. Припускаючи, що сигнал є синусоїдою, потужність сигналу дорівнює квадрату середньоквадратичної амплітуди:

\[power(s)=\left ( \frac{1}{\sqrt{2}} \right )^{2}=\frac{1}{2} \nonumber \]

На малюнку 5.4.2 деталізовано єдиний інтервал квантування.

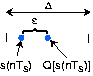
Рисунок 5.4.2 Показаний єдиний інтервал квантування разом із типовим значенням сигналу до квантування амплітуди **s (nT _s)** та після **Q (****s (nT _s)**. ε *позначає понесену таким чином похибку.*

Його ширина дорівнює\(Δ\) і похибка квантування позначається\(\varepsilon\). Щоб знайти потужність в похибці квантування, відзначимо, що незалежно від того, в який інтервал квантування потрапляє значення сигналу, помилка буде мати ті ж характеристики. Щоб обчислити середньоквадратичне значення, ми повинні квадратувати похибку і усереднити її за інтервал.

\[\begin{align*} rms(\varepsilon) &=\sqrt{\frac{1}{\Delta }\int_{-\Delta }^{\Delta }\varepsilon ^{2}d\varepsilon } \\[4pt] &=\left ( \frac{\Delta ^{2}}{12} \right )^{\frac{1}{2}} \end{align*} \]

Оскільки ширина інтервалу квантування для B-бітового перетворювача дорівнює

\[\dfrac{2}{2^{B}}=2^{-(B-1)} \nonumber \]

ми знаходимо, що відношення сигнал/шум для процесу аналого-цифрового перетворення дорівнює

\[SNR=\frac{\frac{1}{2}}{\frac{2^{-(2(B-1))}}{12}}=\frac{3}{2}2^{2B}=6B+\log 1.5dB \nonumber \]

Таким чином, кожне бітове збільшення A/D перетворювача дає збільшення співвідношення сигнал/шум на 6 дБ. Постійний термін 10 log1.5 дорівнює 1,76.

Вправа\(\PageIndex{1}\)

Це виведення припускало, що амплітуда сигналу лежала в діапазоні [-1,1]. Яким було б відношення сигнал-шум квантування амплітуди, якби воно лежало в діапазоні [-A, A]?

Рішення

Відношення сигнал/шум не залежить від амплітуди сигналу. З A/D діапазоном [-A, A] інтервал квантування

\[\Delta =\frac{2A}{2^{B}} \nonumber \]

і середньоквадратичне значення сигналу (знову припускаючи, що це синусоїда)

\[\frac{A}{\sqrt{2}} \nonumber \]

Вправа\(\PageIndex{2}\)

Скільки бітів потрібно в A/D перетворювачі, щоб гарантувати, що помилка квантування максимальної амплітуди менше 60 дБ менше пікового значення сигналу?

Рішення

Рішення

\[2^{-B}=0.001 \nonumber \]

результати в

\[B=10\; bits \nonumber \]

Вправа\(\PageIndex{3}\)

Музика на компакт-диску зберігається з точністю до 16 біт. Якому співвідношенню сигнал/шум це відповідає?

Рішення

16-бітний A/D перетворювач дає SNR

\[6\times 16+10\log 1.5=97.8dB \nonumber \]

Після того, як ми придбали сигнали за допомогою A/D перетворювача, ми можемо обробляти їх за допомогою цифрового обладнання або програмного забезпечення. Можна показати, що якщо комп'ютерна обробка є лінійною, результат вибірки, комп'ютерної обробки та недискретизації еквівалентний деякій аналоговій лінійній системі. Навіщо йти на все турбувати, якщо одну і ту ж функцію можна виконати за допомогою аналогових прийомів? Знати, коли цифрова обробка перевершує, а коли - ні, є важливим питанням.