5.3: Теорема вибірки
- Page ID
- 32882
- Перетворення між сигналом і цифрами.
Аналого-цифрове перетворення
Через те, як організовані комп'ютери, сигнал повинен бути представлений кінцевою кількістю байтів. Це обмеження означає, що як вісь часу, так і вісь амплітуди повинні бути квантовані: кожен з них повинен бути кратним цілим числам. 1 Досить дивно, що теорема вибірки дозволяє квантувати вісь часу без помилок для деяких сигналів. Сигнали, які можуть бути відібрані без введення помилок, цікаві, і, як описано в наступному розділі, ми можемо зробити сигнал «semplable» шляхом фільтрації. На відміну від цього, ніхто не знайшов способу виконання кроку квантування амплітуди без введення невиправної помилки. Таким чином, значення сигналу більше не може бути будь-яким дійсним числом. Сигнали, оброблені цифровими комп'ютерами, повинні бути дискретними: їх значення повинні бути пропорційні цілим числам. Отже, аналого-цифрове перетворення вносить помилку.
Теорема вибірки
Цифрова передача інформації та цифрова обробка сигналів вимагають, щоб сигнали спочатку «придбані» комп'ютером. Одним з найдивовижніших і корисних результатів в електротехніці є те, що сигнали можуть бути перетворені з функції часу в послідовність чисел без помилок: Ми можемо перетворити числа назад в сигнал з (теоретично) без помилок. Гарольд Найквіст, інженер Bell Laboratories, вперше отримав цей результат, відомий як теорема відбору проб, у 1920-х роках. Тоді він не знайшов реального застосування. Клод Шеннон, також в Bell Laboratories, відродив результат після того, як комп'ютери були оприлюднені після Другої світової війни.
Вибіркова версія аналогового сигналу s (t) є s (nT s), з T відомий як інтервал вибірки. Зрозуміло, що значення вихідного сигналу під час дискретизації зберігається; питання полягає в тому, як значення сигналу між зразками можуть бути реконструйовані, оскільки вони втрачаються в процесі вибірки. Щоб охарактеризувати вибірку, ми наближаємо його як продукт:
\[x(t)=s(t)P_{T_{s}}(t) \nonumber \]
при цьому P T s є періодичним імпульсним сигналом. Отриманий сигнал, як показано на малюнку 5.3.1, має ненульові значення тільки протягом часових інтервалів:
\[\left ( nT_{s}-\frac{\Delta }{2}, nT_{s}+\frac{\Delta }{2}\right ),n\in \left \{ ...,-1,0,1,... \right \} \nonumber \]
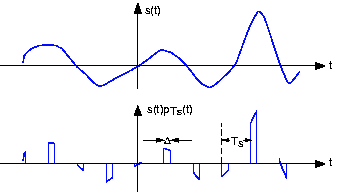
Для наших цілей тут ми центруємо періодичний імпульсний сигнал про походження так, щоб його коефіцієнти ряду Фур'є були дійсними (сигнал парний).
\[P_{T_{s}}(t)=\sum_{k=-\infty }^{\infty }c_{k}e^{\frac{i2\pi kt}{T_{s}}} \nonumber \]
\[c_{k}=\frac{\sin \left ( \frac{\pi k\Delta }{T_{s}}\right )}{\pi k} \nonumber \]
Якщо властивості s (t) та періодичного імпульсного сигналу обрані правильно, ми можемо відновити s (t) з x (t) шляхом фільтрації.
Щоб зрозуміти, як можуть бути «заповнені» значення сигналу між зразками, нам потрібно обчислити спектр вибіркового сигналу. Використовуючи подання рядів Фур'є періодичного сигналу дискретизації,
\[x(t)=\sum_{k=-\infty }^{\infty }c_{k}e^{\frac{i2\pi kt}{T_{s}}}s(t) \nonumber \]
Розглядаючи кожен член в сумі окремо, нам потрібно знати спектр добутку комплексної експоненції і сигналу. Оцінити це перетворення безпосередньо досить легко.
\[\int_{-\infty }^{\infty }s(t)e^{\frac{i2\pi kt}{T_{s}}}e^{i2\pi ft}dt=\int_{-\infty }^{\infty }s(t)e^{-\left ( i2\pi \left ( f-\frac{k}{T_{s}} \right )\right )}dt=S\left ( f-\frac{k}{T_{s}} \right ) \nonumber \]
Таким чином, спектр вибіркового сигналу складається з зважених (за коефіцієнтами c k) і затриманих версій спектра сигналу Малюнок 5.3.2 нижче.
\[X(f)=\sum_{-\infty }^{\infty }c_{k}S\left ( f-\frac{k}{T_{s}} \right ) \nonumber \]
Загалом, терміни в цій сумі перекривають один одного в частотній області, що робить відновлення вихідного сигналу неможливим. Це неприємне явище відоме як згладжування.
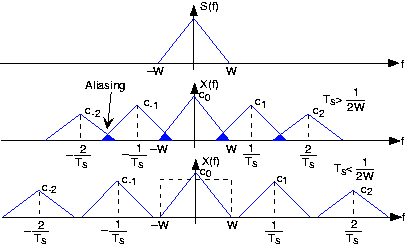
Якщо, однак, ми задовольняємо дві умови:
- Сигнал s (t) обмежений діапазоном - має потужність в обмеженому діапазоні частот - до Вт Гц
- інтервал вибірки T s досить малий, щоб окремі компоненти в сумі не перекривалися - T s < 1/2 W
Згладжування не відбудеться. У цьому чудовому випадку ми можемо відновити вихідний сигнал шляхом фільтрації низьких частот x (t) з фільтром, що має частоту зрізу, рівну W Гц. Ці дві умови забезпечують можливість відновлення сигналу з обмеженою смугою з його вибіркової версії: Таким чином, ми маємо теорему вибірки.
Теорема вибірки (як зазначено) не згадує ширину імпульсу Δ. Який вплив цього параметра на нашу здатність відновлювати сигнал зі своїх зразків (якщо дотримані дві умови Теореми вибірки)?
Рішення
Єдиний ефект тривалості імпульсу полягає в нерівній вазі спектральних повторень. Оскільки ми стурбовані лише повторенням, орієнтованим на походження, тривалість імпульсу не має значного впливу на відновлення сигналу з його зразків.
Частота 1/2T s, відома сьогодні як частота Найквіста та частота дискретизації Шеннона, відповідає найвищій частоті, при якій сигнал може містити енергію і залишатися сумісним з теоремою вибірки. Високоякісні системи вибірки гарантують, що ніякого згладжування не відбувається шляхом безцеремонної фільтрації сигналу низьких частот (частота зрізу трохи нижча за частоту Nyquist) перед вибіркою. Таким чином, такі системи змінюють частоту зрізання фільтра згладжування, оскільки частота дискретизації змінюється. Оскільки такі якісні функції коштують грошей, багато звукових карт не мають фільтрів згладжування або, якщо на те пішло, фільтрів після дискретизації. Вони вибірки на високих частотах, наприклад, 44.1 кГц, і сподіваюся, що сигнал не містить частот вище частоти Найквіста (22,05 кГц в нашому прикладі). Якщо, однак, сигнал містить частоти, що перевищують частоту Nyquist звукової карти, отримане згладжування неможливо видалити.
Щоб отримати кращу оцінку згладжування, намалюйте спектр вибіркової квадратної хвилі. Для простоти розглянемо лише спектральні повторення з центром\[-\frac{1}{T_{s}},0,\frac{1}{T_{s}} \nonumber \]
Нехай інтервал вибірки T s дорівнює 1; розглянемо два значення для періоду квадратної хвилі: 3.5 і 4. Зверніть увагу, зокрема, де спектральні лінії йдуть у міру зменшення періоду; деякі рухатимуться вліво, а деякі вправо. Яке властивість характеризує ті, що йдуть в одному напрямку?
Рішення
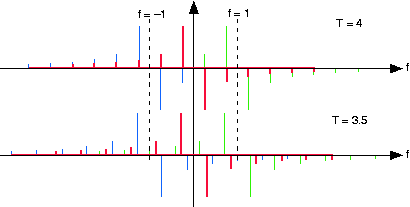
Спектр квадратної хвилі показаний більш сміливою сукупністю ліній, зосереджених щодо початку. Пунктирні лінії відповідають частотам, про які відбуваються спектральні повторення (за рахунок вибірки з T s = 1). Коли період квадратної хвилі зменшується, негативні частотні лінії рухаються вліво, а позитивні частотні - вправо.
Якщо ми задовольняємо умовам Теореми вибірки, сигнал буде змінюватися лише незначно під час кожного імпульсу. Як ми звужуємо пульс, роблячи
Який найпростіший сигнал з обмеженою смугою? Використовуючи цей сигнал, переконайте себе, що менше двох зразків/періоду буде недостатньо для його вказівки. Якщо частота дискретизації 1/T s недостатньо висока, яким сигналом стане ваш отриманий сигнал із заниженою дискретизацією?
Рішення
Найпростішим сигналом, обмеженим смугою, є синусоїда. На частоті Nyquist відбуватимуться рівно два зразки/період. Зменшення частоти дискретизації призведе до меншої кількості пробок/періоду, і ці зразки, як видається, виникли з синусоїди нижчої частоти.
- Припускаємо, що ми не використовуємо A/D перетворювачі з плаваючою комою.
