3.6: Щільність, питомий об'єм, питома вага та питома вага

Last updated
Save as PDF

Page ID: 34375

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Як ми продемонстрували раніше, маса системи є великою властивістю, і як така вона залежить від ступеня системи. Нагадаємо, що для зазначеної системи масу системи можна обчислити з цього загального співвідношення:\[m_{sys}=\int_{V_{sys}} \rho \ dV \nonumber \] неможливо було б скласти таблицю мас для всіх можливих комбінацій речовин і систем, але доцільно скласти таблицю або надати моделі щільності. Як тільки ця інформація стане відомою, це рівняння можна використовувати для обчислення маси системи.

Щільність і питомий об'єм

Щільність речовини зазвичай міститься в таблицях в довідниках як функція речовини і його стану (тобто його температури і тиску). \(\rho\)Щільність речовини - це маса на одиницю об'єму і зазвичай має одиниці\(\mathrm{kg} / \mathrm{m}^{3}\) або\(\mathrm{lbm} / \mathrm{ft}^{3}\).

Математично щільність у точці простору може розглядатися як граничне значення маси на одиницю об'єму в межах невеликого куба об'єму, оскільки обсяг зменшується до нуля:\[\rho = \lim_{\Delta V \rightarrow 0} \frac{m}{\Delta V} \nonumber \] Уявіть, якщо хочете, що коли куб об'єму стає все меншим і меншим, щільність наближається до деякого граничного значення (Див. Малюнок\(\PageIndex{1}\)). У якийсь момент обсяг куба стає досить малим, щоб кількість молекул в межах об'єму починає коливатися з часом. Як тільки ця точка буде досягнута, ідея статистично значущого середнього значення (або межі) не має сенсу.

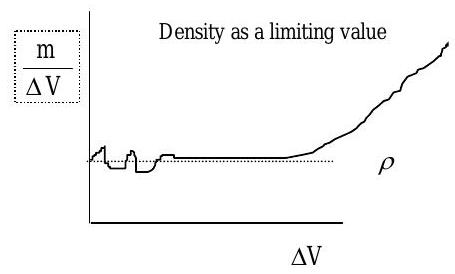
Графік з дельта-об'ємом на осі x та масою над дельтою V на осі Y. При дуже малих значеннях Delta V графік дико коливається, при трохи більших значеннях він залишається близьким до горизонтальної лінії, що представляє щільність, а при більших значеннях піднімається по стійкій кривій.

Малюнок\(\PageIndex{1}\): Щільність як граничне значення.

У цьому курсі ми обмежуємося умовами, за яких можливий цей тип статистично значущого середнього. Це називається припущенням континууму. Іноді цю точку зору також називають макроскопічною точкою зору, оскільки вона стосується лише макроскопічних змінних, таких як тиск, температура, щільність тощо Однією з відмінних переваг макроскопічної або континуальної точки зору є те, що ми не повинні явно розглядати мікроскопічну поведінку атоми і молекули. У цьому курсі ми будемо розглядати лише континууми та макроскопічну точку зору. Іноді нам може бути корисним взяти мікроскопічну точку зору, щоб допомогти нам зрозуміти деякі явища. Хоча в більшості промислових ситуацій припущення континууму є доречним, існує багато важливих ситуацій, коли припущення континууму руйнується. Це, як правило, умови з дуже низькою щільністю, наприклад, умови вакууму, умови в космосі біля краю земної атмосфери.

Для деяких речовин табулюється не щільність, а питомий обсяг. Питомий обсяг\(v\) - це обсяг на одиницю маси. Зазвичай він задається нижнім регістрам «v» як його символ і може бути пов'язаний з щільністю рівнянням:\[v=\frac{1}{\rho} \nonumber \] Розміри для конкретного обсягу є\([\mathrm{L}]^{3} / [\mathrm{M}]\), а типовими одиницями для конкретного об'єму є\(\mathrm{m}^{3} / \mathrm{kg}\) або\(\mathrm{ft}^{3} / \mathrm{lbm}\).

Як і слід було очікувати, існує молярна щільність, визначена як молі на одиницю об'єму та задана символ\(\bar{\rho}\), де накладна вказує, що це кількість на основі молів. Молярний питомий об'єм також визначається аналогічно як обсяг на одиницю моль і дається символ\(\bar{v}\).

Якими були б одиниці для цих двох молярних величин в СІ та в американській інженерній системі?

Питома вага

Питома вага речовини - це вага на одиницю об'єму. Питома вага зазвичай дається символом\(\gamma\) («гамма») і може бути розрахована як добуток щільності на місцеве прискорення сили тяжіння:\[\gamma=\rho g \nonumber \] Будь-які значення питомої ваги, які ви знайдете в таблиці, мають, за необхідності, передбачається значення для локального прискорення сили тяжіння. Якщо не зазначено інше, табличні значення питомої ваги базуються на стандартному значенні для прискорення сили тяжіння на рівні моря,\(9.80665 \mathrm{~m} / \mathrm{s}\) або\(32.174 \mathrm{ft} / \mathrm{s}\). Типовими одиницями для питомої ваги є\(\mathrm{N} / \mathrm{m}^{3}\) або\(\mathrm{lbf} / \mathrm{ft}^{3}\).

Питома вага

У багатьох додатках важливо знати щільність або питому вагу речовини щодо еталонної речовини.. Питома вага\( ( \boldsymbol{SG} )\) речовини - це відношення щільності речовини при заданих умовах до щільності еталонної речовини:\[S G=\frac{\rho}{\rho_{\text{ref}}} \nonumber \] Для рідин і твердих речовин еталонною речовиною є вода,\(4^{\circ} \mathrm{C}\) де щільність води\(1000 \mathrm{~kg} / \mathrm{m}^{3}\) або \(1.940 \ \mathrm{slug} / \mathrm{ft}^{3}\). Для газів еталонним речовиною є повітря з заданою температурою і тиском, скажімо,\(25^{\circ} \mathrm{C}\) і 1 атм. У цих умовах повітря можна розглядати як ідеальний газ.