11.5: Вправи
- Page ID
- 35323
Розглянемо літак, що летить на постійній висоті\(h\), як показано на малюнку 11.21. Припустимо, що Земля обертається з кутовою швидкістю\(\vec{\Omega}_E = \Omega \cdot \vec{k}_E\), а вітру немає (спокійні умови). Припустимо, що літак оснащений інерційною навігаційною системою страпоном. За часом\(t\) акселерометри і гіроскопи забезпечують наступні вимірювання:
- Кутова швидкість:\(\vec{W} = W_x \cdot \vec{i}_b + W_y \cdot \vec{j}_b + W_z \cdot \vec{k}_b \approx 0\).
- Прискорення кузова кадру: 18\(\vec{a}_b = a_x \cdot \vec{i}_b + a_y \cdot \vec{j}_b + a_z \cdot \vec{k}_b\).
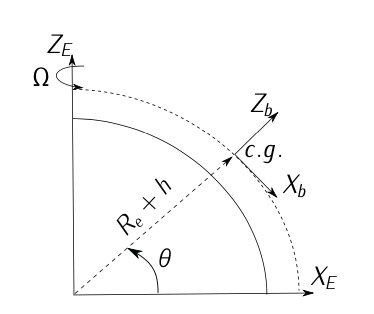
Малюнок 11.19: Інерційна навігаційна система (вправа 3.1)
Розглянемо:
- літак летить зі\(\vec{V} = V \cdot \vec{i}_b\) швидкістю в часі\(t\).
- кут\(\theta\) можна вважати приблизно постійним.
Отримати:
- символічне вираження термінів прискорення\(a_x\)\(a_z\),\(a_y\) і, ідентифікуючи ті, які обумовлені рухом літака по відношенню до Землі і ті, які обумовлені інерційними і гравітаційними ефектами.
- Підставляємо, використовуючи наведені нижче значення і надаємо значення (і напрямок) прискорення літака по відношенню до Землі:
\(\bullet\)\(\Omega = 1\ rev./day\).
\(\bullet\)\(W_x \approx 0; W_y \approx 0\)
\(\bullet\)\(a_x = 0.9831\ m/s^2; a_y = 0.0257\ m/s^2, a_z = -9.8269\ m/s^2\).
\(\bullet\)\(V = 250\ m/s; h = 11.000\ m\).
\(\bullet\)\(R_E = 6378\ km; g = 9.81\ m/s^2\).
\(\bullet\)\(\theta = 45\ deg\).
- Відповідь
-
Почнемо говорити, що абсолютне прискорення тіла є\(\vec{a}_i = \tfrac{d^2 \vec{r}}{dt^2}|_i\), а швидкість тіла є\(\vec{V}_i = \tfrac{d\vec{r}}{dt}|_i\), будучи\(i\) кадром інерційної системи відліку (наприклад, фіксованою зіркою) і\(\vec{r}\) радіовектором і\(t\) часом.
Потім, згідно з другим законом Ньютона:\(m \cdot \tfrac{d^2 \vec{r}}{dt^2}|_i = \sum \vec{F}_{ext}\), будучи\(m\) масою тіла і\(F_{ext}\) зовнішніми силами.
Використовуючи формулу Коріоліса, можна сказати, що похідна на узагальненій векторній величині (\(\vec{A}\)) в абсолютних вираженнях (щодо інерційної системи відліку\(i\)) дорівнює її похідній у відносних вираженнях (щодо неінерційної системи відліку\(e\)) плюс векторний добуток відносна кутова швидкість двох кадрів (\(\vec{w}_{ei}\)) та загальна векторна величина\(\vec{A}\). У порядку слів:
\[\dfrac{d\vec{A}}{dt}|_i = \dfrac{d\vec{A}}{dt}|_e + \vec{w}_{ei} \wedge \vec{A}\label{eq11.5.1}\]
Таким чином, можна сказати, що:
\[\dfrac{d\vec{r}}{dt}|_i = \dfrac{d\vec{r}}{dt}|_e + \vec{w}_{ei} \wedge \vec{r}\]
Прийом похідних:
\[\dfrac{d^2\vec{r}}{dt^2}|_i = \dfrac{d^2\vec{r}}{dt^2}|_e + \dfrac{d}{dt}[\vec{w}_{ei} \wedge \vec{r}]\]
Це призводить до:
\[\dfrac{d\vec{V}}{dt}|_i = \dfrac{d\vec{V}}{dt}|_e + \vec{w}_{ei} \wedge \vec{V}\label{eq11.5.4}\]
Іншими словами, абсолютні члени дорівнюють відносним чинам плюс Коріолісові терміни. Можна також сказати, що:
\[\dfrac{d^2\vec{r}}{dt^2}|_i = \dfrac{d}{dt} (\dfrac{d\vec{r}}{dt}|_i)|_i = \dfrac{d}{dt} (V + \vec{w}_{ei} \wedge \vec{r})|_i,\]
яка розробка дає:
\[\dfrac{d^2\vec{r}}{dt^2}|_i = \dfrac{d\vec{V}}{dt}|_i + \dfrac{d}{dt}(\vec{w}_{ei} \wedge \vec{r})|_i\label{eq11.5.6}\]
Рівняння (\(\ref{eq11.5.6}\)) також називають рівнянням навігації. Ми можемо застосувати формулу Коріоліса in (\(\ref{eq11.5.1}\)) до першого члена правої сторони в Equation (\(\ref{eq11.5.6}\)), який дає,\(\tfrac{d\vec{V}}{dt}|_e + \vec{w}_{ei} \wedge \vec{V}|_e\) як у Eq. (\(\ref{eq11.5.4}\)), і до другого члена правої сторони в Рівняння (\(\ref{eq11.5.6}\)), який дає\(\tfrac{d(\vec{w}_{ei} \wedge \vec{r})}{dt} + \vec{w}_{ei} \wedge (\vec{w}_{ei} \wedge \vec{r})\). Таким чином, ур. (\(\ref{eq11.5.6}\)) призводить до:
\[\vec{a} |_i = \vec{a}|_e + 2 \cdot \vec{w}_{ei} \wedge \vec{V} + \vec{w}_{ei} \wedge (\vec{w}_{ei} \wedge \vec{r}),\label{eq11.5.7}\]
де\(\vec{V}\) і\(\vec{r}\) є величинами, що відносяться до неінерційної системи відліку\(e\).
Рівняння (\(\ref{eq11.5.7}\)) - добре відомий склад рівняння прискорень. У контексті навігації він стверджує, що абсолютне прискорення (щодо інерційної системи відліку i) дорівнює відносному прискоренню (щодо неінерційної системи відліку e, як правило, Землі) плюс ефекти Коріоліса (другий термін у правій частині (\(\ref{eq11.5.7}\))) і відцентрові ефекти (третій термін у правій частині (\(\ref{eq11.5.7}\))).
У контексті аналізованої задачі прискорення, виміряне інерційною одиницею вимірювання, є абсолютними (\(\vec{a}_b\)), включаючи гравітаційні ефекти та інерційні (Коріолісові та відцентрові) умови. Однак, щоб в подальшому обчислити положення літака по відношенню до Землі (\(vec{a}_e\)), нас цікавить відносне прискорення, тобто прискорення тіла (літака) по відношенню до Землі. Іншими словами:
\[\vec{a}_b = \vec{a}_e + \vec{g} + Coriolis + Centrifugal\]
Давайте тепер попрацюємо над кожним з цих термінів. Спочатку визначте наступні вектори:
\[\vec{g} = -g \cdot \vec{k}_b\]
\[\vec{w}_{ei} = \Omega \cdot \vec{k}_e\]
\[\vec{r} = (R_e + h) \cdot \vec{k}_b\]
\[\vec{V} = V \cdot \vec{i}_b\]
Тоді, працюючи, один має:
\[Coriolis: 2 \Omega V \sin \theta \cdot \vec{j}_b\]
\[Centrifugal: -\Omega^2 (R_e + h) \cos \theta \cdot \vec{i}_e\]
\[Gravity: -g \cdot \vec{k}_b.\]
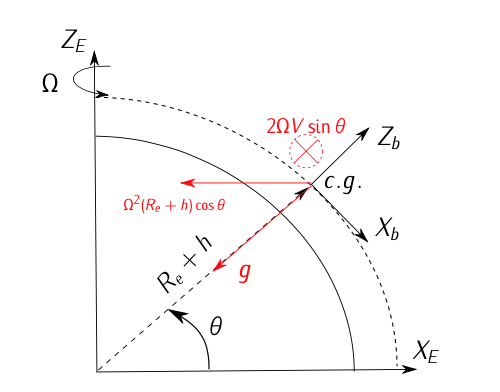
Малюнок 11.20: Інерційна навігаційна система, включаючи гравітаційне прискорення, прискорення Коріоліса (\(2\Omega V\)) та відцентрове прискорення (\(\Omega^2 (R_e + h) \cos (\theta)\)).Будь ласка, див. Рисунок 11.20.
Ми повинні спроектувати відцентровий термін на вісь кузова-рама:
\[Centrifugal: -\Omega^2 (R_e + h) \cos \theta \cdot (\sin \theta \cdot \vec{i}_b + \cos \theta \cdot \vec{k}_b)\]
Тоді ми можемо сказати:
\[a_x \cdot \vec{i}_b = (a_{ex} - \Omega^2 (R_e + h) \cos \theta \sin \theta) \cdot \vec{i}_b,\]
\[a_y \cdot \vec{j}_b = (a_{ey} + 2\Omega V \sin \theta) \cdot \vec{j}_b,\]
\[a_z \cdot \vec{k}_b = (a_{ez} - g - \Omega^2 (R_e + h) \cos^2 \theta) \cdot \vec{k}_b,\]
де\(a_{ex}\)\(a_{ey}\), і\(a_{ez}\) є прискореннями літака по відношенню до Землі і\(a_x\)\(a_y\), і\(a_z\) є абсолютними прискореннями, виміряними ІМУ.
Дайте нам знати, зокрема до заданих значень, в результаті чого:
\[a_x \cdot \vec{i}_b = (a_{ex} - 0.0168941032554) \cdot \vec{i}_b,\]
\[a_y \cdot \vec{j}_b = (a_{ey} + 0.0257111281143) \cdot \vec{j}_b,\]
\[a_z \cdot \vec{k}_b = (a_{ez} - -9.82689410326) \cdot \vec{k}_b.\]
При вимірах акселерометрів є, і\(a_x = 0.9831\ m/s^2\), відповідно\(a_y = 0.0257\ m/s^2\)\(a_z = -9.8269\ m/s^2\), один має: Дайте нам знати, particularize до заданих значень, в результаті чого:
\[a_{ex} \cdot \vec{i}_b \approx 1 \cdot \vec{i}_b\]
\[a_{ey} \cdot \vec{j}_b \approx 0 \cdot \vec{j}_b\]
\[a_{ez} \cdot \vec{k}_b \approx 0 \cdot \vec{k}_b\]
Таким чином, прискорення літака по відношенню до Землі,\(\vec{a}_e = 1 \cdot \vec{i}_b \ m/s^2\). Це прискорення є тим, яке слід використовувати для отримання положення літака за допомогою подвійної інтеграції (з огляду на певні початкові умови).
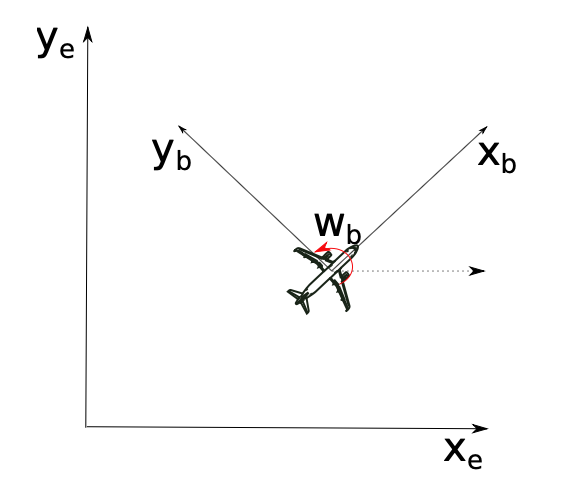
Малюнок 11.21: Ескіз INS.
Розглянемо літак, що летить на постійній висоті, як показано на малюнку 11.21. Припустимо, Землю можна вважати плоскою, що не обертається, 19 і вітру немає (спокійні умови). Припустимо, що літак оснащений інерційною навігаційною системою страпоном. За часом\(t\) акселерометри і гіроскопи забезпечують наступні вимірювання:
- Кутова швидкість:\(\vec{w}_b = w \cdot \vec{k} \approx 0\).
- Сили кузова-рами:\(\vec{f}_b = (f_{bx} \cdot \vec{i}_b, f_{by} \cdot \vec{j}_b)\).
З огляду на наступні початкові умови:
- початковий кут нахилу/колії:\(\theta_0\);
- початковий час:\(t_0\);
- вихідне положення:\(\vec{r}_0 = (x_0 \cdot \vec{i}_e, y_0 \cdot \vec{j}_e)\);
- початкова швидкість:\(\vec{v}_0 = (v_0 \cdot \vec{i}_b, 0 \cdot \vec{j}_b)\);
Розрахувати:
- Положення літака на час\(t\).
- Відповідь
-
Перш за все, читач повинен помітити, що, припускаючи необертову Землю, ми не розглядаємо інерційні (Коріолісові і Відцентрові) терміни. Також, оскільки рух вважається горизонтальним, гравітація не грає ніякої ролі в цій проблемі. Звичайно, реалістична проблема інерційної навігації вимагатиме проведення аналізу в попередній вправі. Для простоти ми зосереджуємося тут на інтеграції прискорень для отримання позиції (чогось не вистачає в попередній вправі).
Зверніть увагу\(\vec{w} = \dot{\theta}\), що, будучи\(\theta\) довільним кутом між фіксованим напрямком\(\vec{i}_e\), наприклад, і колією літака, тобто\(\vec{i}_b\).
Таким чином, ми можемо отримати варіацію з\(\theta\) часом\(\theta (t)\), просто інтегруючи поточне рівняння:
\[\int_{\theta_0}^{\theta} d\theta = \int_{t_0}^{t} w(t) dt \to \theta (t).\label{eq11.5.26}\]
Тепер, оскільки вимірювання гіроскопа можна наблизити до нуля\(\vec{w} \approx 0\), тобто рівняння\(\ref{eq11.5.26}\) дає:
\[\theta = \theta_0.\]
Ремінні акселерометри забезпечують вимірювання абсолютних сил на осі каркаса тіла, які можуть бути легко (за умов, припускаються тут) трансформуються в прискореннях, тобто\(\vec{a}_b = (a_{bx} \cdot \vec{i}_b, a_{by} \cdot \vec{j}_b)\).
Тепер, щоб висловити абсолютне прискорення в системі відліку Землі, нам потрібно просто застосувати обертання:
\[\begin{bmatrix} \vec{a}_{ex} \\ \vec{a}_{ey} \end{bmatrix} = \begin{bmatrix} \cos \theta_0 & -\sin \theta_0 \\ \sin \theta_0 & \cos \theta_0 \end{bmatrix} \cdot \begin{bmatrix} \vec{a}_{bx} \\ \vec{a}_{by} \end{bmatrix}\]
Ми тепер, що:
\[\dfrac{d\vec{V}}{dt} = \vec{a};\]
\[\dfrac{d\vec{r}}{dt} = d \vec{V}.\]
Інтегруючи один раз, ми отримуємо:
\[v_x = v_0 + (a_{xb} \cdot \cos \theta_0 - a_{yb} \cdot \sin \theta_0) \cdot t\]
\[v_y = (a_{yb} \cdot \sin \theta_0 + a_{xb} \cdot \cos \theta_0) \cdot t\]
Інтегруючи двічі, ми отримуємо:
\[x = x_0 + v_0 \cdot t + (a_{xb} \cdot \cos \theta_0 - a_{yb} \cdot \sin \theta_0 ) \cdot \dfrac{t^2}{2}\]
\[y = y_0 + (a_{yb} \cdot \sin \theta_0 + a_{xb} \cdot \cos \theta_0) \cdot \dfrac{t^2}{2}\]
Зверніть увагу, що\(t\) передбачається досить малий (дійсно, еквівалентний частоті вимірювання) таким чином, що вимірювання можна вважати постійними вздовж часового інтервалу.
18. заради простоти припускаємо, що акселерометри безпосередньо забезпечують прискорення після того, як виміряли сили і зробили відповідні перетворення.
19. Можна припустити, що як відцентрові, так і Коріолісові терміни нехтуються у формулі, яка стосується абсолютного та відносного прискорення. Іншими словами, абсолютні і відносні прискорення можна вважати ідентичними. Зверніть увагу, що це вірно тут, тому що ми вважали Землю не обертається.
