9.5: Вправи

Вправа\(\PageIndex{1}\) Traffic Demand

Вправа пов'язана з генеральним плануванням аеропортів. Студенти об'єднаються в групи по чотири людини кожна. Вправа повинна бути виконана під час заняття. Студентам дозволяється використовувати будь-які засоби, наприклад, книги, ноутбуки, інтернет, щоб знайти рішення проблеми.

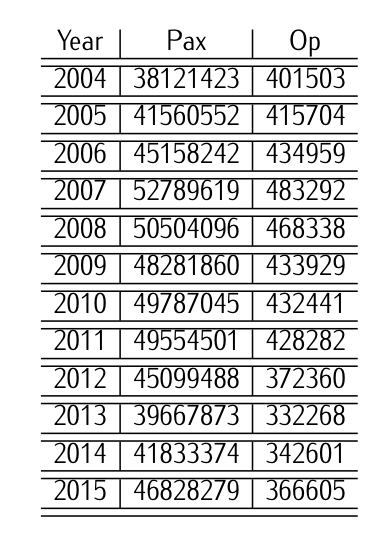
Таблиця 9.7: Історичні дані [2004-2015 період] про кількість пасажирів і кількість операцій в аеропорту Мадрид-Барахас Адольфо-Суареса.

Надаються історичні дані, що містяться в таблиці 9.7 з кількістю пасажирів і кількістю операцій в аеропорту Мадрид-Барахас Адольфо-Суареса за період 2004-2015 років.

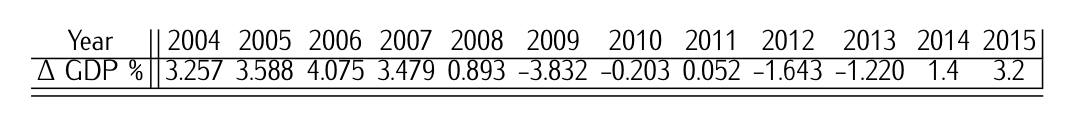
Таблиця 9.8: Історичні дані [період 2004-2015 рр.] зростання ВВП.

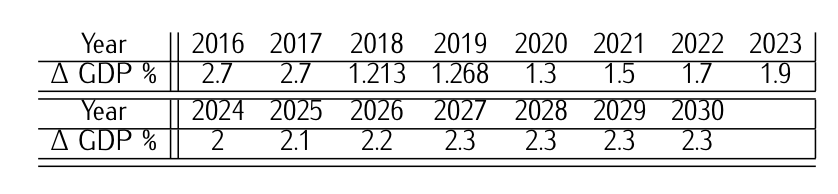
Таблиця 9.9: Прогноз [2016-2030] зростання ВВП.

Історичні дані [період 2004-2015 рр.] іспанського валового внутрішнього продукту (ВВП) [в номінальному вираженні, тобто без урахування інфляції] наведені в таблиці 9.8. Також прогнози прогнозу світового ВВП на 2016-2030 роки [в номінальному вираженні] як від МВФ (Міжнародний валютний фонд), так і CEPREDE7 наведені в таблиці 9.9.

1. За допомогою цих даних (Pax і ВВП) зробіть прогноз трафіку (кількість чол. 2016-2030) за допомогою економетричних моделей. Знайдіть рішення (прогноз трафіку) для трьох різних сценаріїв (песимістичний, номінальний, оптимістичний). Зобразити ескіз фігури еволюції кількості пасажирів в період 2016-2030 років за трьома сценаріями.

Максимальна пропускна здатність аеропорту Адольфо-Суарес Мадрид Барахас була оголошена як 70 мільйонів пасажирів на рік.

2. За різними прогнозами, коли, за оцінками, аеропорт не здатний впоратися з попитом пасажирів?

3. На які ще показники слід звернути увагу (крім загальної кількості пасажирів), щоб проаналізувати пропускну здатність аеропорту? Чому?

Відповідь

Економетричні моделі є однією з найскладніших і найскладніших методик прогнозування попиту в аеропортах. Часто застосовуються прості та множинні методи регресійного аналізу (лінійний та нелінійний).

Множинний регресійний аналіз можна розглядати як розширення простого лінійного регресійного аналізу (який включає лише одну незалежну змінну) до ситуації, коли розглядаються дві або більше незалежних змінних. Загальна форма поліноміальної регресійної моделі для m незалежних змінних дорівнює

\[Y = \beta_0 + \beta_1 X_1+ \beta_2 X_2 + ... + \beta_m X_m + \varepsilon,\]

де\(\beta_0, \beta_1, ..., \beta_m\) - коефіцієнти регресії, які необхідно оцінити. Незалежні змінні\(X_1, X_2,... , X_m\) можуть бути окремими базовими змінними, або деякі з них можуть бути функціями декількох базових змінних. \(Y\)являє собою індивідуальне спостереження і\(\varepsilon\) є компонентом помилки, що відображає різницю між спостережуваною реакцією індивіда\(Y\) та справжньою середньою відповіддю\(\mu_{Y|X_1,X_2,...,X_m}\).

У цьому конкретному випадку для простоти виконуємо лінійний регресійний аналіз наступним чином:

\[Y = \beta_0 + \beta_1 X_1 + \varepsilon,\]

де\(Y\) представляє окремі спостереження, тобто значення попиту на перевезення (pax) між 2004-2015 роками; і\(X_1\) являє собою пояснювальні змінні, тобто зростання валового внутрішнього продукту за той же період. Тому ми хочемо оцінити\(\beta_0\) коефіцієнти,\(\beta_1\) які найкраще відповідають даним; іншими словами, ми хочемо оцінити лінію, яка мінімізує помилки\(\varepsilon\) спостережень. Ми будемо використовувати метод мінімальних квадратів.

Беручи 2004-2015 роки, рішення полягає в наступному:

\[Y = -0.1307 + 2.7182 X,\label{eq9.5.3}\]

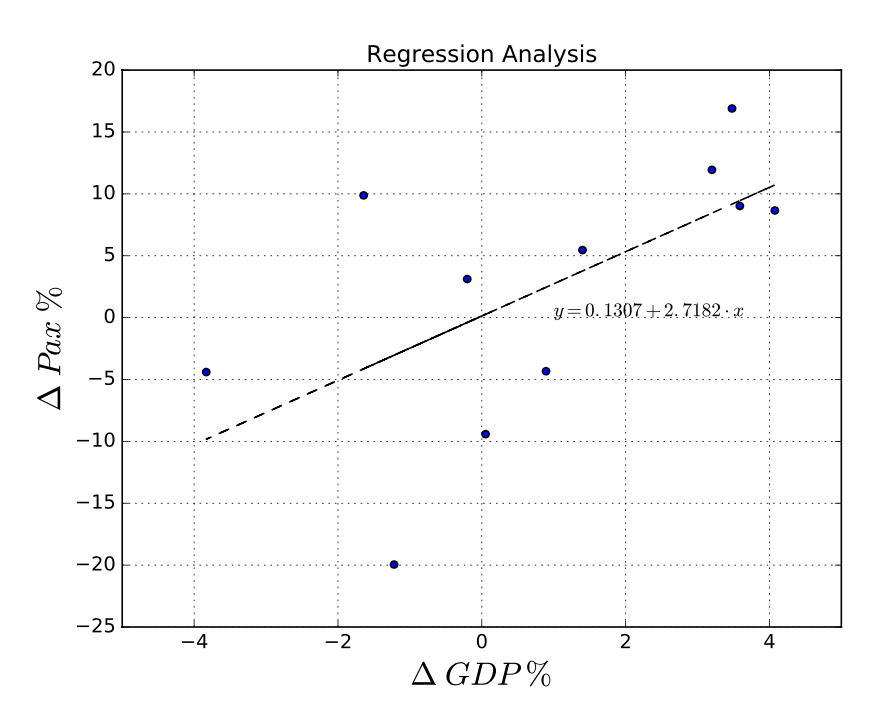
Малюнок 9.17: Лінійний регресійний аналіз.

де\(Y\) представляють де% зростання пасажирів, а X - відсоток зростання ВВП. Див. Малюнок 9.17. Доброгідність придатності, виміряна через R2 (коефіцієнт детермінації), досить низька (0,6080), що означає, що крива не дуже добре підходить до даних (як це можна спостерігати з графіка). Може бути зроблена інша регресія, в якій деякі спостереження можна вважати викидами або навіть розглядати нелінійні функції.

З огляду на Eq. (\(\ref{eq9.5.3}\)), будуємо три різних сценарії зростання ВВП: номінальний (наведено в таблиці 9.8), оптимістичний (в даному випадку той, що наведено в таблиці 9.8 + 0,5%), і песимістичний (в даному випадку той, що наведено в таблиці 9.8 - 0,5%). Знову ж таки, зверніть увагу, що інші сценарії могли бути побудовані, що дає різні результати.

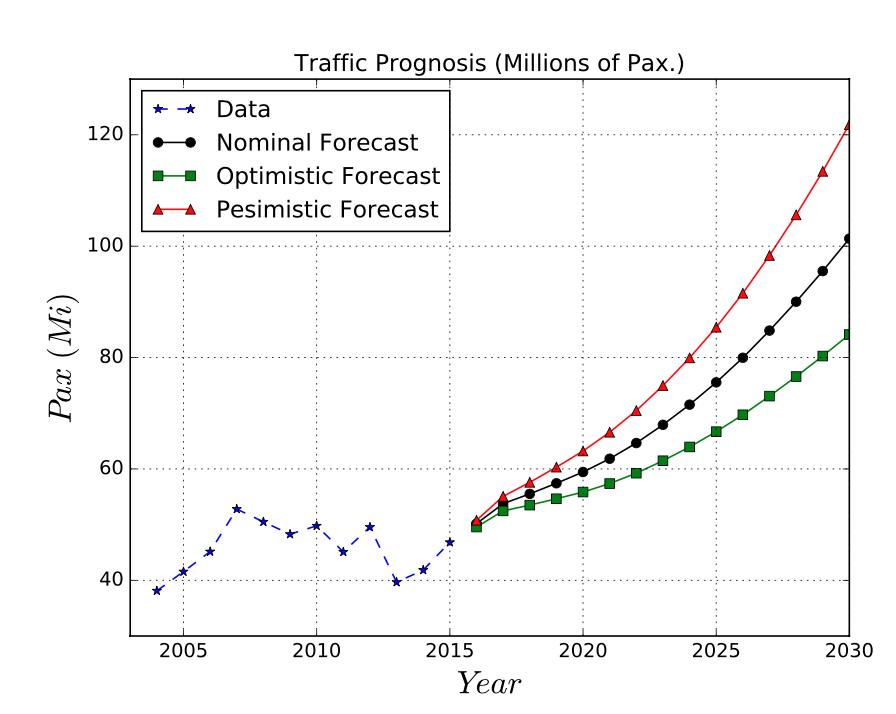
Малюнок 9.18: Сценарії прогнозування трафіку.

2. Коли вважається, що аеропорт не здатний впоратися з попитом пасажирів?

• Песимістичний: 70 млн. Пакс перевищив у 2026 році.
• Номінальний: 70M Pax перевищив у 2023 році.
• Оптимістично: 70 млн. Пакс перевищив у 2021 році.

 

3. На які ще показники слід звернути увагу (крім загальної кількості пасажирів), щоб проаналізувати пропускну здатність аеропорту? Чому?

Слід також подивитися на години роботи/проектування; PAX/Час проектування. Крім того, кількість транспортних засобів, що під'їхали до аеропорту; кількість людей, які користуються метрополітеном і т.д.

 

Вправа\(\PageIndex{2}\) Wind Rose

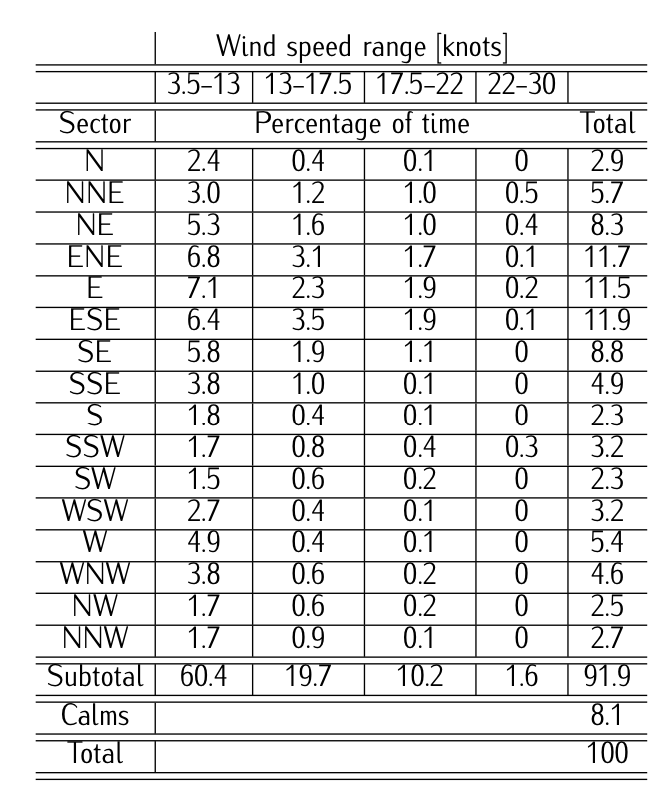
Таблиця 9.10: Приклад історичних даних про вітер.

Для даного сайту, розташованого в Somewhere, історичні дані про вітер вже зібрані за останні 15 років, як показано в таблиці 9.10.

1. Заповніть схему троянди вітрів, намальовану нижче, і запропонуйте найбільш підходящий напрямок (або напрямки) для нової злітно-посадкової смуги (або злітно-посадкових смуг).

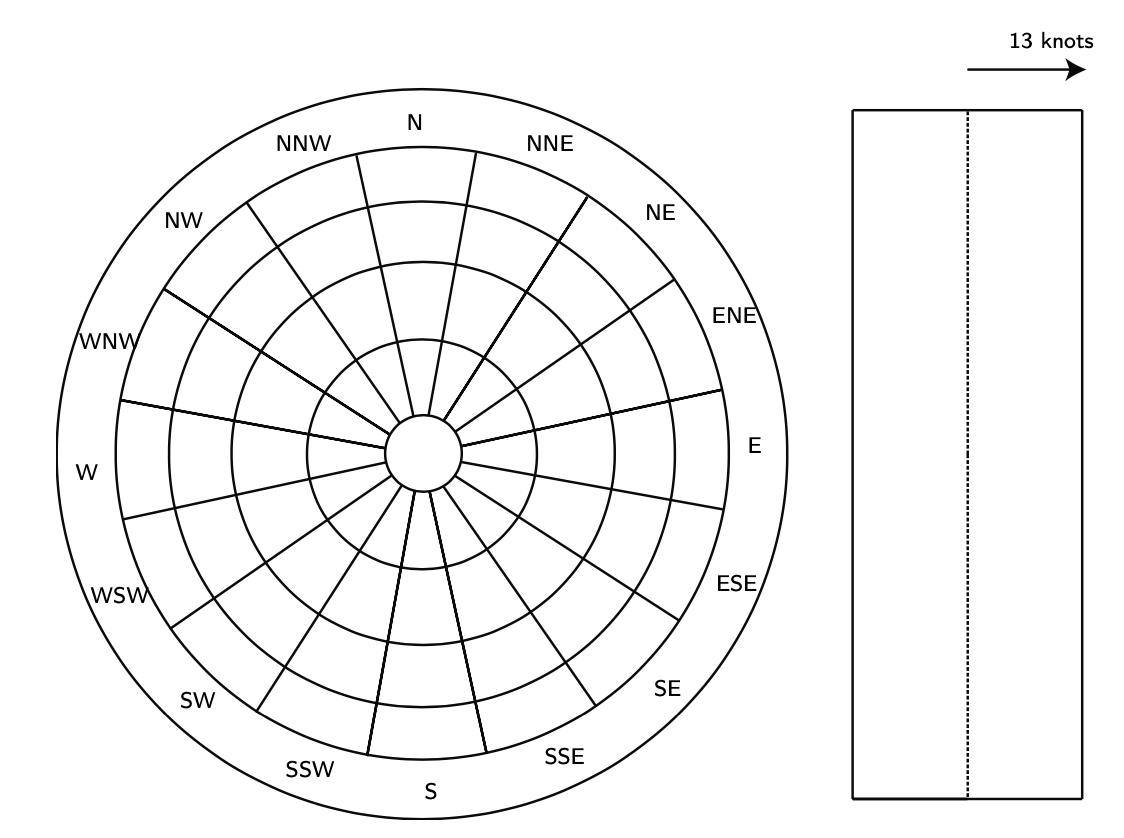
Малюнок 9.19: Система координат і шаблон «Роза вітрів» з обмеженнями компонентів поперечного вітру 13 вузлів.

Відповідь

Відповідно до Додатку 14 ІКАО (Рекомендація 3.1):

Кількість і орієнтація злітно-посадкових смуг на аеродромі повинні бути такими, щоб коефіцієнт юзабіліті аеродрому становив не менше 95 відсотків для літаків, які призначений обслуговувати аеродром.

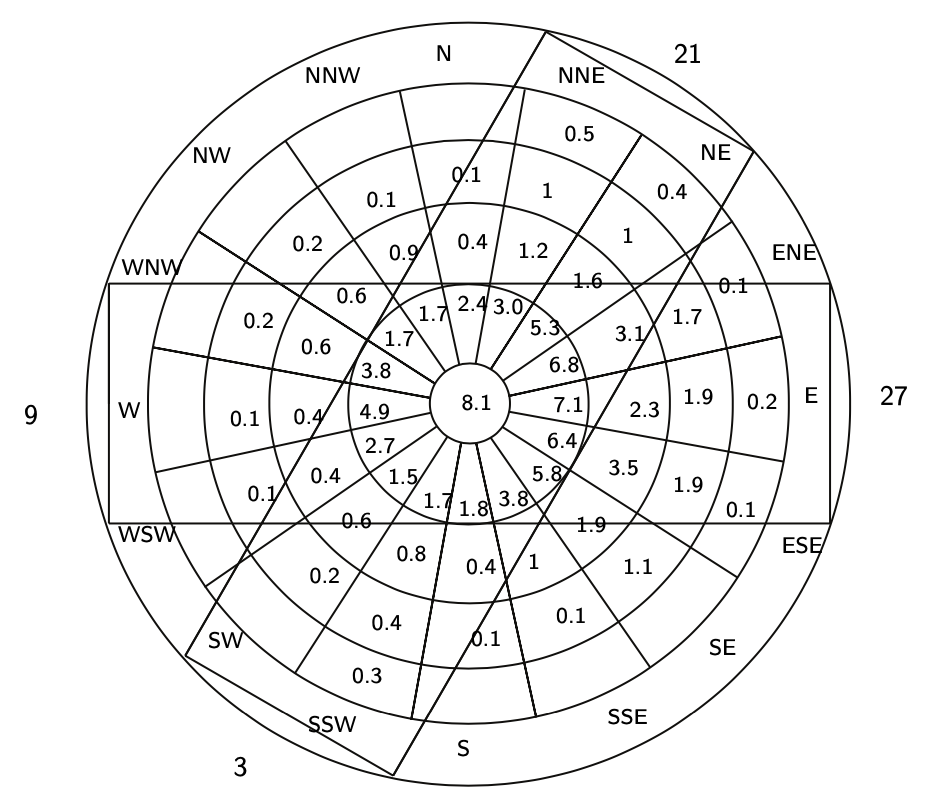
Малюнок 9.20: Вітрове покриття для злітно-посадкових смуг 9-27 і 3-21.

Потім, беручи до уваги цю рекомендацію, ми спочатку обчислюємо орієнтацію злітно-посадкової смуги, що дає максимальний відсоток вітру між паралельними лініями. Це злітно-посадкова смуга 9-27 (див. Рис. Це дозволить близько 90-91% операцій. Якщо хтось хоче слідувати рекомендаціям, ми повинні побудувати ще одну злітно-посадкову смугу. Ми робимо це, намагаючись максимізувати% операцій. Рішення - злітно-посадкова смуга 3-21 (див. Рис. 9.20), яка дозволила б близько 97,5% операцій.

Вправа\(\PageIndex{3}\) Aerodrome data

Вправа пов'язана з визначенням основних даних аеродрому для конкретного аеропорту. Для аеропорту Адольфо Суареса Мадрид Барахас, визначити:

1. Наступні дані про сайт:

• Орієнтир аеродрому;
• Піднесення аеродрому;
• Координати порогів злітно-посадкової смуги;
• Координати паркувальних положень;
• Середня висота кожного з порогів;
• Підйом голів злітно-посадкової смуги;
• Максимальна висота зони приземлення;

Відповідь

З усіма даними можна ознайомитися в AENA AIS Адольфо Суареса Мадрид Барахас. Зокрема, слід проконсультуватися:

• Дані аеродрому
• Діаграма аеродрому
• Аеродром наземний рух діаграми
• Літак паркування/стикування діаграми
• Діаграма перешкод аеродрому

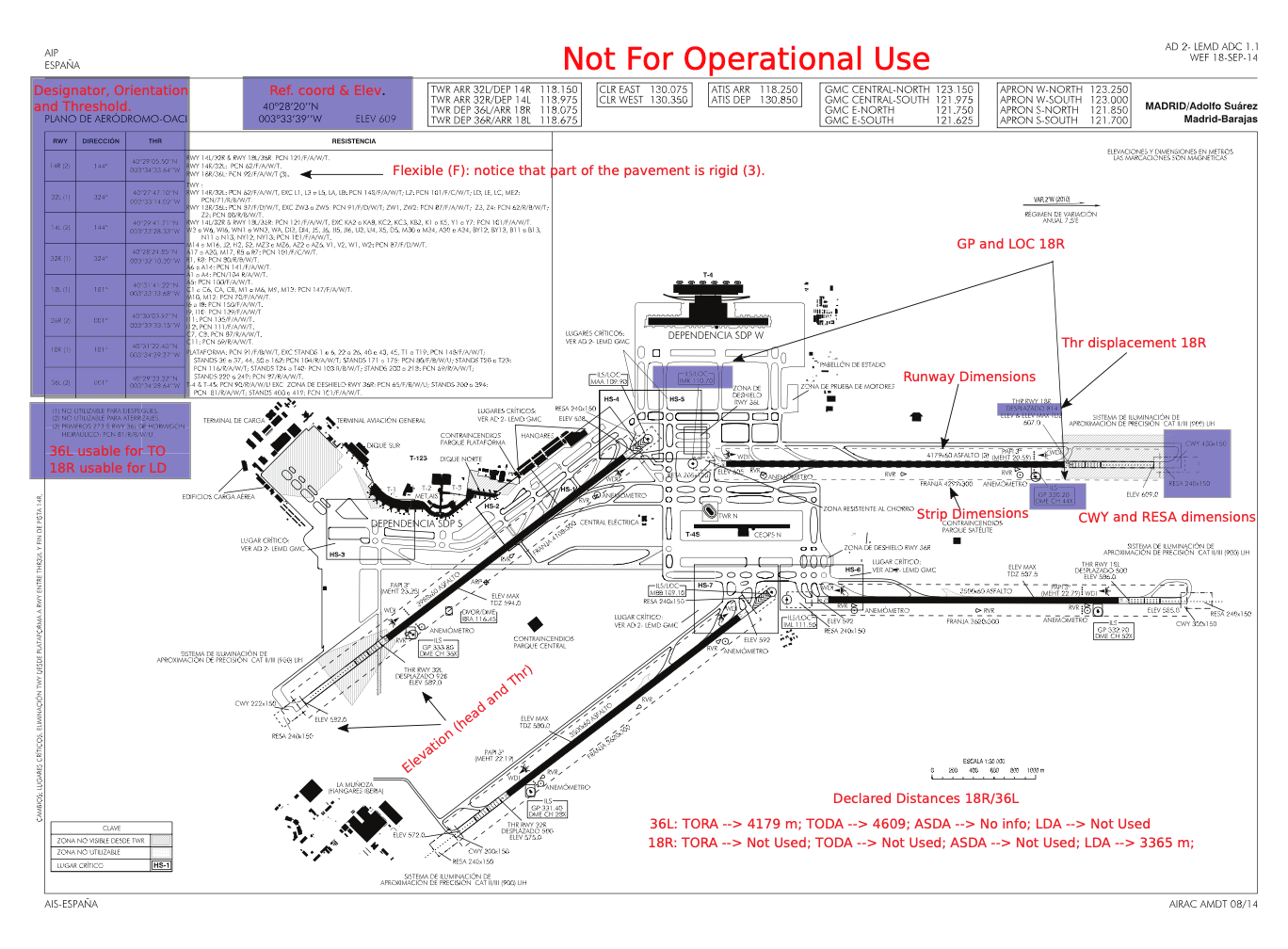
Малюнок 9.21: Дані аеродрому.

Рішення накидається на малюнку 9.21. Будь ласка, зверніть увагу, що рішення вправи 9.4 також наведено на цьому малюнку.

Вправа\(\PageIndex{4}\) Airfield data

Вправа пов'язана з визначенням основних даних аеродрому для конкретного аеропорту. Для аеропорту Адольфо Суарес Мадрид Барахас (Для злітно-посадкової смуги 36L/14R) ідентифікують наступні дані про зону пересування:

• Розміри (довжина і ширина);
• Юзабіліті як 36L, так і 18R для зльотів і посадок.
• Зони безпеки (зони безпеки смуги та злітно-посадкової смуги для 36L/18R);
• Зсув порога на 36л і 18Р;
• Заявлені відстані для 36L і 18R;
• Визначте локалізатор і шлях ковзання для ILS злітно-посадкової смуги 18R. Запишіть їх частоти.
• Класифікація тротуарів Кількість злітно-посадкових смуг 36L та 18R. Що це за тротуар? Як ми можемо це знати?

З усією цією інформацією можна ознайомитися на карті аеродрому Мадрид-Барахас Адольфо Суареса, наведеній у додатку.

Відповідь

 

З усіма даними можна ознайомитися в AIS AIS Адольфо Суарес Мадрид Барахас, консультуючись з тими ж документами, що і у вправі 1.3. Рішення накидається на малюнку 9.21.

 

Вправа\(\PageIndex{5}\) Airfield Design

Регіональний аеропорт, який буде спроектований, має такі характеристики розміщення:

• Розташований на рівні моря;
• Розміщений в рівнинній місцевості;
• Розташований в стандартній широті 40 град (\(\Delta T = 0\)).

Критичний літак має такі характеристики:

• Посилання Довжина поля\ (\ to\ 0 1100 м.
• Розмах крил\(\to\) 28 м.

Зробіть ескізний проект злітно-посадкової смуги відповідно до правил ICAO в додатку 14. Виконайте наступні дії (при необхідності використовуйте ескізи):

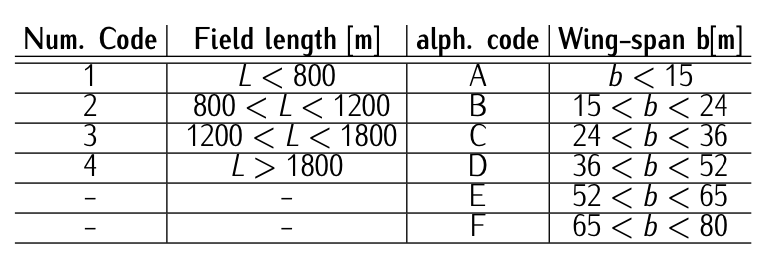
Таблиця 9.11: Категорії злітно-посадкової смуги ІКАО (алф. код відноситься до типу літака).

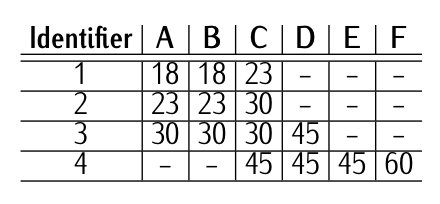
Таблиця 9.12: Мінімальна ширина злітно-посадкової смуги [м] ідентифікатори ІКАО.

1. Визначити еталонний код аеродрому (див. Таблицю 9.11);

2. Вибрати довжину і ширину злітно-посадкової смуги (див. Таблицю 9.12);

3. Розміри зон безпеки (смуга і злітно-посадкова смуга кінця зони безпеки);

4. Визначте позначення двох головок злітно-посадкової смуги відповідно до напрямку злітно-посадкової смуги, обраного в попередній вправі.

5. Оберіть одну з голів злітно-посадкової смуги та змістіть поріг на 100 м. Опублікуйте заявлені відстані голови цієї злітно-посадкової смуги (зверніть увагу, що необхідно враховувати зупинку та проріз; при необхідності розмірність їх дотримується рекомендацій ІКАО).

Необхідну інформацію можна знайти в таблицях нижче та в додатку, що містить додаток 14 ІКАО (3.10-3.17).

Відповідь

 

Малюнок 9.22: Дизайн злітно-посадкової смуги

1. Довідковий код аеродрому буде 2С.
2. З огляду на, що висота аеродрому дорівнює 0, умови стандартні ISA, а нахилу немає, відстань повинна бути заданою опорним полем критичного літака (1100 м). Будь-яка велика злітно-посадкова смуга також буде працювати, але передбачає надмірне інвестування Ширина також повинна бути мінімальною (30 м) з тієї ж причини.
3. Розміри повинні бути не менше: смуги (1220 м\(\times\) 180 м) і RESA (60 м\(\times\) 90 м), починаючи з краю голови злітно-посадкової смуги. Влада рекомендує RESA довжиною 120 м для інструментального аеродрому.
4. Позначення були б 05 і 23.
5. Повинна бути Clearway (довжина менше, ніж у злітного прогону шириною\(\times\) 75 м від центральної лінії); Стопвей не є обов'язковим, але він повинен мати ту ж ширину, що і злітно-посадкова смуга. Будь ласка, перевірте Рисунок 9.22 для вирішення проблеми.
6. Заявлені відстані також можна перевірити на малюнку 9.22. Зверніть увагу, що в разі SWY довжина злітно-посадкової смуги повинна бути 1100 + SWY. Тоді ASDA буде 1100 + SWY.

 

Вправа\(\PageIndex{6}\) Visual aids data

Вправа пов'язана з визначенням основних наочних посібників аеродрому для конкретного аеропорту. Для аеропорту Адольфо Суареса Мадрид Барахас, визначити:

1. основна розмітка будь-якої з злітно-посадкових смуг, тобто:

   \(\bullet\)Позначення
   \(\bullet\) Поріг і передпоріг
   \(\bullet\) Центральні лінії і бічна лінія
   \(\bullet\) Прицільна точка Зона
   \(\bullet\) приземлення

2. основні вогні будь-якої з злітно-посадкових смуг.

3. інструментальні допоміжні засоби на аеродромі, тобто VOR, DME, ILS. Запишіть місце розташування і частоту.

4. основна розмітка в руліжних доріжках.

5. основна розмітка в фартусі і пандусі.

Відповідь

З усіма даними можна ознайомитися в AENA AIS Адольфо Суареса Мадрид Барахас. Зокрема, слід проконсультуватися:

• Дані аеродрому
• Діаграма аеродрому
• Аеродром наземний рух діаграми
• Літак паркування/стикування діаграми

Вправа\(\PageIndex{7}\) Visual aids design

Вправа є продовженням вправи 9.5.5, пов'язаного таким чином з попереднім проектом злітно-посадкової смуги. Припустімо, що ви зробили попередній проект злітно-посадкової смуги, включаючи розміри, зони безпеки тощо (тобто припустимо, що ви оцінили вправу 9.5.5). Робіть ескізний проект основної розмітки злітно-посадкової смуги, тобто:

• Позначення
• Поріг і передпоріг
• Осьові лінії і бічна лінія
• Точка прицілювання
• Зона приземлення

і основні вогні злітно-посадкової смуги.

Відповідь

З усіма даними можна ознайомитися в додатку 14 ІКАО та посібнику з проектування злітно-посадкової смуги ІКАО (Частина I та IV).

Вправа\(\PageIndex{8}\) Take-off length calculation

Ми хочемо оцінити відстань зльоту типового комерційного реактивного літака. На таких літальних апаратах монтуються два турбореактивні апарати\(T = T_0 (1 − k \cdot V^2)\), тягу яких можна оцінити як:, де\(T\) тяга,\(T_0\) є номінальною тягою,\(k\) є постійною і\(V\) є справжньою повітряною швидкістю.

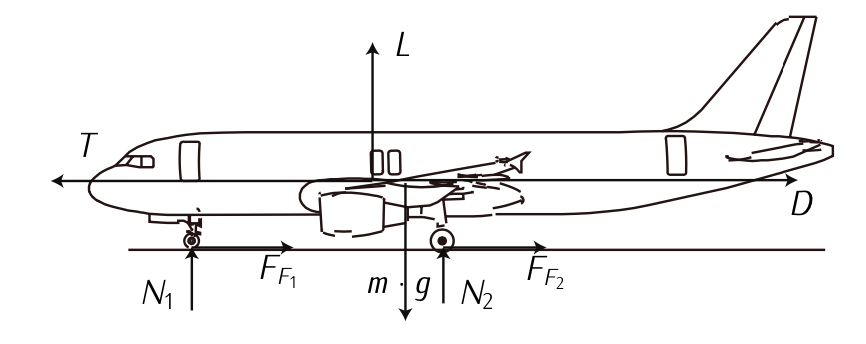
Малюнок 9.23: Сили під час зльоту біжать.

Розглянемо рис. 9.23, де\(g\) сила, зумовлена гравітацією,\(m\) це маса літака,\(F_F\) відповідає силі тертя (будучи\(\mu_r\) коефіцієнтом тертя дорожнього покриття),\(L\) і\(D\) є силою підйому і опору, відповідно, які можуть бути виражені як :

\[L = C_L \dfrac{1}{2} \rho SV^2;\]

\[D = C_D \dfrac{1}{2} \rho SV^2;\]

де\(\rho\) - щільність повітря,\(S\) - площа вологої поверхні\(C_D\) літака, - коефіцієнт опору (який можна наблизити до паразитного коефіцієнта\(C_L\) опору,\(C_D = C_{D_0}\) т. Е. ⁸

Знайти:

1. Аналітичний вираз для злітної відстані цього родового літака.

Розглянемо B-737-800, значення якого можна наблизити до:

• \(T_0 = 149000\ [N]\)і\(k = 1 \cdot 10^{-5}\).
• \(C_{D_0} = 0.0357\)(з конфігурацією заслінки для зльоту)
• \(S = 124.65\ [m^2]\);
• \(m = 78300\ [kg] (MTOW)\);
• \(V_{TO} = 1.2 V_{Stall}\)(з конфігурацією флопа для зльоту). Ми можемо розглянути\(V_{LOF} = 1.1 V_{Stall}\);
• \(V_{stall} = \sqrt{\tfrac{2mg}{\rho S C_{L_{\max}}}}\);
• \(C_{L_{\max}} = 2\)і\(C_L = 0.8 C_{L_{\max}}\).

Більш того, ми можемо розглянути\(\mu_r = 0.025\).

Відповідно до раніше вибраних номерів:

2. Відстань зльоту для різних висот (рівень моря, 2000 футів, 4000 футів, 6000 футів, 8000 футів, 10000 футів) в спокійних умовах та максимальній злітній вазі. Порівняйте ці результати з цифрами, опублікованими в документі 737 Характеристики літака для планування аеропорту. Обговоріть їх.

Відповідь

[1] Ми застосовуємо 2-й Закон Ньютона:

\[\sum F_z = 0;\label{eq9.5.6}\]

\[\sum F_x = m \dot{V}.\label{eq9.5.7}\]

Що стосується Equation (\(\ref{eq9.5.6}\)), зверніть увагу, що під час катання по землі літак вважається рівновагою вздовж вертикальної осі.

Дивлячись на рисунок 9.23, Рівняння (\(\ref{eq9.5.6}\)) - (\(\ref{eq9.5.7}\)) стають:

\[L + N - mg = 0;\label{eq9.5.8}\]

\[T - D - F_F = m \dot{V}.\label{eq9.5.9}\]

будучи\(L\) підйом,\(N\) нормальна сила, мг вага;\(T\) довіра,\(D\) опір і\(F_F\) загальна сила тертя.

Загальновідомо, що:

\[L = C_L \dfrac{1}{2} \rho S V^2;\label{eq9.5.10}\]

\[D = C_D \dfrac{1}{2} \rho SV^2.\label{eq9.5.11}\]

Також добре відомо, що:

\[F_F = \mu_r N.\]

Рівняння (\(\ref{eq9.5.8}\)) стверджують, що:\(N = mg - L\). Тому:

\[F_F = \mu_r (mg - L).\label{eq9.5.13}\]

Враховуючи це\(T = T_0 (1 - kV^2)\), з рівнянням (\(\ref{eq9.5.13}\)) та рівняннями (\(\ref{eq9.5.10}\)) - (\(\ref{eq9.5.11}\)). Рівняння (\(\ref{eq9.5.9}\)) стає:

\[(\dfrac{T_0}{m} - \mu_r g) + \dfrac{(\rho S(\mu_r - C_D) - 2T_0 k)}{2m}V^2 = \dot{V}.\label{eq9.5.14}\]

Тепер ми повинні інтегрувати Equation (\(\ref{eq9.5.14}\)).

Для цього ми знаємо, як було зазначено в заяві, що:\(T_0, m, \mu_r, g, \rho, S, C_L, C_D\) і\(k\) може вважатися постійним уздовж фази зльоту.

У нас є, що:

\[\dfrac{dV}{dt} = \dfrac{dV}{dx} \dfrac{dx}{dt},\]

і знаючи це\(\tfrac{dx}{dt} = V\), Рівняння (\(\ref{eq9.5.14}\)) стає:

\ [\ dfrac {(\ tfrac {T_0} {м} -\ mu_r г) +\ tfrac {(\ рхо S (\ mu_r C_L - C_D) - 2T_0k)} {2m} V^2} {V} =\ dfrac {dV} {dx}. \ етикетка {еква9.5.16}\)

Для того, щоб спростити Рівняння (\(\ref{eq9.5.16}\)):

• \((\tfrac{T_0}{m} - \mu_r g) = A\);
• \(\tfrac{(\rho S(\mu_r C_L - C_D) - 2 T_0k)}{2m} = B\).

Ми продовжуємо інтегрувати Equation\(x_{LOF}\) (\(\ref{eq9.5.16}\)) між\(x = 0\) і (відстань підйому);\(V = 0\) (припускаючи, що маневр починається з літака в спокої) і швидкість зльоту:\(V_{LOF}\). Він стверджує, що:

\[\int_{0}^{x_{LOF}} dx = \int_{0}^{V_{LOF}} \dfrac{VdV}{A + BV^2}.\]

інтеграція:

\[\langle x \rangle_0^{x_{LOF}} = \langle \dfrac{1}{2B} Ln (A + BV^2) \rangle_0^{V_{LOF}}\]

Підставляємо верхню і нижню межі:

\[x_{LOF} = \dfrac{1}{2B} Ln (1 + \dfrac{B}{A} V_{LOF}^2).\label{eq9.5.19}\]

[2] Зі значеннями, зазначеними в операторі та використанням Eq (\(\ref{eq9.5.19}\)) та підставляючи його, виходить:

• \(x_{LOF} (h = 0) = 2605.5\ [m]\)
• \(x_{LOF} (h = 2000\ ft) = 2764.4\ [m]\)
• \(x_{LOF} (h = 4000\ ft) = 2935.4\ [m]\)
• \(x_{LOF} (h = 6000\ ft) = 3119.7\ [m]\)
• \(x_{LOF} (h = 8000\ ft) = 33186\ [m]\)
• \(x_{LOF} (h = 10000\ ft) = 3533.4\ [m]\)

Малюнок 9.24 ілюструє це. Якщо подивитися на офіційні документи, то для умов рівня моря можна помітити, що обидва значення схожі. Згідно з малюнком, літак не міг злетіти з\(MTOW\) для висоти вище\(2000\ ft\). Повторюючи аналіз на масу 60 тонн, результати представляють більшу схожість з таблицями.

Вправа\(\PageIndex{9}\) B-737-800 Aircraft Characteristics related to Airport Planning

Для Б-737-800 отримують:

• Загальна характеристика (ваги);
• Загальні розміри;
• Діаграма корисного навантаження;
• Вимоги до злітно-посадкової смуги (рівень моря\(4000\ ft; 8000\ ft\));
• Вимоги до посадки (рівень моря;\(4000\ ft; 8000\ ft\));
• Вимоги до радіусів повороту.

Відповідь

Для вирішення зверніться до посібника з аеропорту B-737-800, до якого можна отримати доступ до характеристик літаків Boeing, пов'язаних з плануванням аеропорту. ⁹

---

8. Зверніть увагу, що\(T_0, k, g, m, \mu_r, S, C_{D_0}\) і\(C_L\) може вважатися постійним під час зльоту.

9. http://www.boeing.com/boeing/commerc...n_manuals.page.