7.3: Проблеми

Вправа\(\PageIndex{1}\) Performances

Розглянемо на Airbus A-320 з наступними характеристиками:

• \(m = 64\ tonnes.\)
• \(S_w = 122.6\ m^2.\)
• \(C_D = 0.024 + 0.0375 C_L^2\).

1. Літак починає маневр підйому з рівномірною швидкістю на висоті 10.000 футів (3048 метрів). На цьому рівні польоту типові показники літака вказують на швидкість по відношенню до повітря 289 вузлів (\(148.67\ m/s\)) і швидкість підйому (вертикальна швидкість)\(2760\ feet/min\) (\(14\ m/s\)). Припускаючи\(\gamma \ll 1\), що, обчислити:
   (а) Кут підйому,\(\gamma\).
   (б) Необхідна тяга при цих умовах.
2. Літак досягає висоти\(11000\ m\) і виконує горизонтальний, стійкий, прямий політ. Визначити:
   (а) швидкість, відповідну максимальному аеродинамічному ККД.
3. Пілот відключає двигуни і починає ковзати на висоті\(11000\ m\). Обчисліть:
   (а) Мінімальна швидкість спуску (вертикальна швидкість) і відповідний кут спуску,\(\gamma_d\):

Відповідь

Крім даних, наведених у заяві, були використані наступні дані:

• \(g = 9.81\ m/s^2\).
• \(R = 287\ J/(kgK)\).
• \(\alpha_T = 6.5 \cdot 10^{-3}\ K/m\).
• \(\rho_0 = 1.225\ kg/m^3\).
• \(T_0 = 288.15\ K\).
• \(ISA: \rho = \rho_0 (1 - \tfrac{\alpha_T h}{T_0})^{\tfrac{gR}{\alpha_T} - 1}\).

1. Рівномірно-підйом при наступних умовах польоту:
   \(\bullet\)\(h = 3048\ m\). Використання\(ISA \to \rho = 0.904\ kg/m^3\).
   \(\bullet\)\(V = 148.67\ m/s\).
   \(\bullet\)\(h_e = 14\ m/s\).
   Система, яка керує рухом літака:
   \[T = D + mg \sin \gamma;\]
   \[L = mg \cos \gamma;\]
   \[\dot{x}_e = V\cos \gamma;\]
   \[\dot{h}_e = V \sin \gamma.\]
   Припускаючи\(\gamma \ll 1\), що, і, таким чином, що\(\cos \gamma \sim 1\) і \(\sin \gamma \sim \gamma\), Система (B.1) стає:
   \[T = D + mg \gamma;\label{eq7.3.5}\]
   \[L = mg;\label{eq7.3.6}\]
   \[\dot{x}_e = V;\]
   \[\dot{h}_e = V_{\gamma}.\label{eq7.3.8}\]
   (а) З рівняння (\(\ref{eq7.3.8}\)),\(\gamma = \tfrac{\dot{h}_e}{V} = 0.094\ rad\ (5.39^{\circ})\).
   (б) З рівняння (\(\ref{eq7.3.5}\)),\(T = D + mg\gamma\).
   \[D = C_D \dfrac{1}{2} \rho S_w V^2,\label{eq7.3.9}\]
   де\(C_D = 0.024 + 0.0375 C_L^2\), і\(\rho, S_w, V^2\) відомі.
   \[C_L = \dfrac{L}{\tfrac{1}{2} \rho S_w V^2} = 0.512,\label{eq7.3.10}\]
   де, згідно з рівнянням (\(\ref{eq7.3.6}\)),\(L = mg\). З рівнянням (\(\ref{eq7.3.10}\)) в рівнянні (\(\ref{eq7.3.8}\)),\(D = 41398\ N\).
   Нарешті:
   \[T = D + mg\gamma = 100\ kN.\nonumber\]
2. Горизонтальний, стійкий, прямий політ при наступних умовах польоту:
   \(\bullet\)\(h = 11000\ m\). Використання\(ISA \to \rho = 0.3636\ kg/m^3\).
   \(\bullet\)Аеродинамічний ККД максимальний.
   Система, яка керує рухом літака:
   \[T = D;\]
   \[L = mg \cos \gamma.\label{eq7.3.12}\]
   Максимальна ефективність є\(E_{\max} = \tfrac{1}{2\sqrt{C_{D_0} C_{D_i}}} = 16.66\).
   Оптимальним коефіцієнтом підйому є\(C_{L_{opt}} = \sqrt{\dfrac{C_{D_0}}{C_{D_i}}} = 0.8\).
   \[C_L = \dfrac{L}{\tfrac{1}{2} \rho S_w V^2} \to V = \dfrac{L}{\tfrac{1}{2} \rho S_w C_L} = 187\ m/s,\nonumber\]
   де, згідно Equation (\(\ref{eq7.3.12}\))\(L = mg\), і для того, щоб літати з максимальною ефективністю:\(C_L = C_{L_{opt}}\).
3. Планування при наступних умовах польоту:
   \(\bullet\)\(h = 11000\ m\). Використання\(ISA \to \rho = 0.3636\ kg/m^3\).
   \(\bullet\)При мінімальній швидкості спуску.
   Система, яка керує рухом літака:
   \[D = mg\sin \gamma_d;\label{eq7.3.13}\]
   \[L = mg \cos \gamma_d;\label{eq7.3.14}\]
   \[\dot{x}_e = V \cos \gamma_d;\label{eq7.3.15}\]
   \[\dot{h}_{e_{des}} = V \sin \gamma_d.\label{eq7.3.16}\]
   Зверніть увагу, що\(\gamma_d = -\gamma\).
   Припускаючи\(\gamma_d \ll 1\), що, і таким чином, що\(\cos \gamma_d \sim 1\) і\(\sin \gamma_d \sim \gamma_d\), System (\(\ref{eq7.3.13}\)\(\ref{eq7.3.14}\),\(\ref{eq7.3.15}\),,\(\ref{eq7.3.16}\)) стає:
   \[D = mg \gamma_d;\label{eq7.3.17}\]
   \[L = mg;\label{eq7.3.18}\]
   \[\dot{x}_e = V;\]
   \[\dot{h}_{e_{des}} = V\gamma_d.\]
   Для того щоб літати з максимальною швидкістю спуску\(\dot{h}_{e_{des}}\) повинна бути максимальною. Робота з рівнянням (\(\ref{eq7.3.17}\)) та рівнянням (\(\ref{eq7.3.18}\)),\(\gamma_d = \tfrac{D}{L}\).
   \[\dot{h}_{e_{des}} = V\gamma = V \dfrac{D}{L} = V \dfrac{(0.024 + 0.0375 C_L^2) \tfrac{1}{2} \rho S_w V^2}{C_L \tfrac{1}{2} \rho S_w V^2}.\label{eq7.3.21}\]
   знаючи\(C_L = \tfrac{L}{\tfrac{1}{2} \rho S_w V^2}\), що де, згідно з рівнянням (\(\ref{eq7.3.18}\))\(L = mg\), Рівняння (\(\ref{eq7.3.21}\)) стає:
   \[\dot{h}_{e_{des}} = \dfrac{V}{mg} \left (0.024 \dfrac{1}{2} \rho S_w V^2 + \dfrac{0.0375 (mg)^2}{\tfrac{1}{2} \rho S_w V^2} \right ).\label{eq7.3.22}\]
   зробити\(\tfrac{\partial \dot{h}_{e_{des}}}{\partial V} = 0\).
   Швидкість по відношенню до повітря так, щоб вертикальна швидкість була мінімальною:
   \[V = \sqrt[4]{\dfrac{4}{3} \dfrac{C_{D_i}}{C_{D_0}}} \sqrt{\dfrac{mg}{\rho S_w}} = 142.57\ m/s.\]
   Підстановка\(V = 142.57\ m/s\) в Рівняння (\(\ref{eq7.3.22}\)),\(\dot{h}_{e_{des}} = 9.87\ m/s\).

Вправа\(\PageIndex{2}\) Runway performances

Ми хочемо оцінити відстань зльоту Airbus A-320, що злітає в аеропорту Мадрид-Барахас. На таких літальних апаратах монтуються два турбореактивні апарати\(T = T_0 (1 - k\cdot V^2)\), тягу яких можна оцінити як:, де\(T\) тяга,\(T_0\) є номінальною тягою,\(k\) є постійною і\(V\) є справжньою повітряною швидкістю.

Враховуючи, що:

• \(g \cdot (\tfrac{T_0}{m\cdot g} - \mu_r) = 1.31725 \tfrac{m}{s^2};\)
• \(\tfrac{\rho S(C_D - \mu_r C_L) + 2 \cdot T_0 \cdot k}{2 \cdot m} = 3.69 \cdot 19^{-5} \tfrac{m}{s^2};\)
• Швидкість зльоту дорівнює\(V_{TO} = 70\ m/s;\)

де\(g\) сила, зумовлена гравітацією,\(m\) - маса\(\mu_r\) літака, - коефіцієнт\(\rho\) тертя, щільність повітря,\(S\) площа мокрій поверхні літака,\(C_D\) це коефіцієнт підйому ⁹.

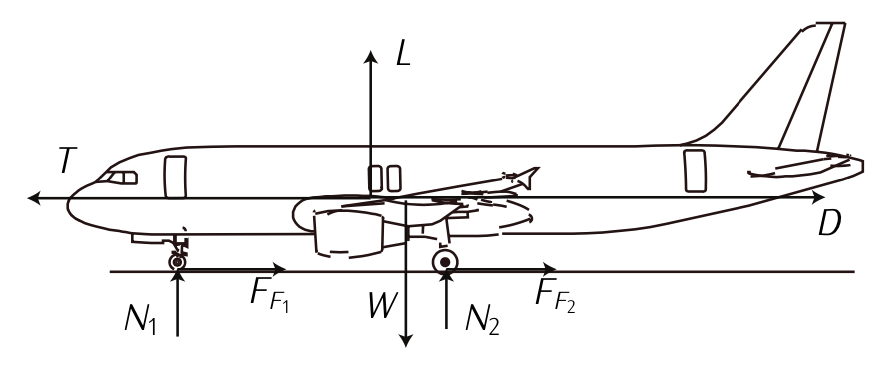
Малюнок 7.16: Сили під час зльоту

Обчисліть:

1. Злітна дистанція.

Відповідь

Застосовуємо 2-й Закон Ньютона:

\[\sum F_z = 0;\label{eq7.3.24}\]

\[\sum F_x = m \dot{V}.\label{eq7.3.25}\]

Що стосується Equation (\(\ref{eq7.3.24}\)), зверніть увагу, що під час катання по землі літак вважається рівновагою вздовж вертикальної осі.

Дивлячись на малюнок 7.16, Рівняння (\(\ref{eq7.3.24}\)) - (\(\ref{eq7.3.25}\)) стане:

\[L + N - mg = 0;\label{eq7.3.26}\]

\[T - D - F_F = m \dot{V}.\]

будучи\(L\) ліфт,\(N\) нормальна сила,\(mg\) вага;\(T\) довіра,\(D\) опір і\(F_F\) загальна сила тертя.

Загальновідомо, що:

\[L = C_L \dfrac{1}{2} \rho S V^2;\label{eq7.3.28}\]

\[D = C_D \dfrac{1}{2} \rho S V^2.\label{eq7.3.29}\]

Також добре відомо, що:

\[F_F = \mu_r N.\]

Рівняння (\(\ref{eq7.3.26}\)) стверджує, що:\(N = mg - L\). Тому:

\[F_F = \mu_r (mg - L).\label{eq7.3.31}\]

Враховуючи\(T = T_0 (1 - kV^2)\), що з рівнянням (\(\ref{eq7.3.31}\)) та рівняннями (\(\ref{eq7.3.28}\)) - (\(\ref{eq7.3.29}\)) рівняння (9.5.9) стає:

\[\right (\dfrac{T_0}{m} -\mu_r g \right) + \dfrac{(\rho S (\mu_r C_L - C_D) - 2T_0 k)}{2m} V^2 = V.\label{eq7.3.32}\]

Тепер ми повинні інтегрувати Equation (\(\ref{eq7.3.32}\)).

Для цього, як зазначено в заяві:\(T_0, m, \mu_r, g, \rho, S, C_L, C_D\) і\(k\) може вважатися постійним уздовж фази зльоту.

У нас є, що:

\[\dfrac{dV}{dt} = \dfrac{dV}{dx} \dfrac{dx}{dt},\]

і знаючи\(\tfrac{dx}{dt} = V\), що, Рівняння (\(\ref{eq7.3.32}\)) стає:

\[\dfrac{(\tfrac{T_0}{m} - \mu_r g) + \tfrac{(\rho S (\mu_r C_L - C_D) - 2T_0 k)}{2m} V^2}{V} = \dfrac{dV}{dx}.\label{eq7.3.34}\]

Для того, щоб спростити Equation (\(\ref{eq7.3.34}\)):

• \((\tfrac{T_0}{m} - \mu_r g) = g(\tfrac{T_0}{mg} - \mu_r) = A;\)
• \(\tfrac{(\rho S (\mu_r C_L - C_D) - 2T_0 k)}{2m} = B.\)

Ми продовжуємо інтегрувати рівняння\(x_{T0}\) (\(\ref{eq7.3.34}\)) між\(x = 0\) і (відстань зльоту);\(V = 0\) (Припускаючи, що маневр починається з літака в спокої) і швидкості зльоту, яка була дана в заяві:\(V_{TO} = 70\ m/s\). Він стверджує, що:

\[\int_{0}^{x_{TO}} dx = \int_{0}^{V_{TO}} \dfrac{VdV}{A+ BV^2}.\]

Інтеграція:

\[\left [ x \right ]_{0}^{x_{TO}} = \left [ \dfrac{1}{2B} \ln (A + BV^2) \right ]_{0}^{V_{TO}}.\]

Підставляємо верхню і нижню межі:

\[x_{TO} = \dfrac{1}{2B} \ln (1 + \dfrac{B}{A} V_{TO}^2).\]

Підставляємо дані, наведені в заяві:

• \(A = 1.31725 \tfrac{m}{s^2};\)
• \(B = -3.69 \cdot 10^{-5} \tfrac{m}{s^2};\)
• \(V_{TO} = 70\ m/s.\)

Відстань до зльоту - це\(x_{TO} = 2000\ m\).

Вправа\(\PageIndex{3}\) Performances

Літак має такі характеристики:

• \(S_w = 130\ m^2\).
• \(b = 40\ m\).
• \(m = 70000\ kg\).
• \(T_{\max, av} (h = 0) = 120000\ N\)(Максимально доступна тяга на рівні моря).
• \(C_{D_0} = 0.02\).
• Коефіцієнт Освальда (коефіцієнт корисної дії крила):\(e = 0.9\).
• \(C_{L_{\max}} = 1.5\).

Ми можемо вважати, що максимальна тяга змінюється тільки в залежності від висоти наступним чином:\(T_{\max, av} (h) = T_{\max, av} (h = 0) \tfrac{\rho}{\rho_0}\). Враховуйте стандартну атмосферу\(ISA\) і постійну гравітацію\(g = 9.8\ m/s^2\). Визначте:

1. Необхідна тяга для польоту на висоті\(h = 11000\ m\) з\(M_{\infty} = 0.7\) в горизонтальному, стійкому, прямому польоті.

2. Максимальна швидкість обумовлена силовими обмеженнями літака і відповідним числом Маха в горизонтальному, стійкому, прямому польоті в\(h = 11000\).

3. Мінімальна швидкість обумовлена аеродинамічними обмеженнями (стійла швидкість) при горизонтальному, стійкому, прямому польоті на висоті\(h = 11000\).

4. Теоретичний стелю (максимальна висота) в горизонтальному, стійкому, прямому польоті.

Ми хочемо виконувати горизонтальний поворот на висоті\(h = 11000\) з коефіцієнтом навантаження\(n = 2\), і зі швидкістю, відповідною максимальній аеродинамічній ефективності при горизонтальному, стійкому, прямому польоті. Визначте:

5. Необхідний кут банку.

6. Радіус повороту.

7. Необхідна тяга. Чи може літак виконати повний поворот?

Ми хочемо виконати горизонтальний поворот з тим же коефіцієнтом навантаження і таким же радіусом, як і в попередньому випадку, але на висоті, відповідній теоретичному стелі літака.

8. Чи може літак виконати такий поворот?

Відповідь

Крім даних, наведених у заяві, були використані наступні дані:

• \(R = 287\ J/(kgK)\).
• \(\gamma_{air} = 1.4.\)
• \(\alpha_T = 6.5 \cdot 10^{-3} \ K/m\).
• \(\rho_0 = 1.225 \ kg/m^3\).
• \(T_0 = 288.15\ K\).
• \(ISA: \rho = \rho_0 (1 - \tfrac{\alpha_T h}{T_0})^{\tfrac{gR}{\alpha_T} - 1}.\)

1. Необхідна тяга для польоту горизонтальним, стійким, прямим польотом при наступних умовах польоту:
   \(\bullet\)\(h = 11.000\ m\);
   \(\bullet\)\(M_{\infty} = 0.7.\)
   згідно\(ISA\):
   \(\bullet\)\(\rho (h = 11000) = 0.364\ Kg/m^3\);
   \(\bullet\)\(a (h = 11000) = \sqrt{\gamma_{air} R (T_0 - \alpha_T h)} = 295.04\ m/s\).
   де a відповідає швидкості звуку.
   Система, яка керує динамікою літака, є:
   \[T = D;\label{eq7.3.37}\]
   \[L = mg;\label{eq7.3.38}\]
   бути\(L\) підйомом,\(mg\) вагою;\(T\) довірою та\(D\) перетягуванням.
   Добре відомо, що:
   \[L = C_L \dfrac{1}{2} \rho S_w V^2;\label{eq7.3.39}\]
   \[D = C_D \dfrac{1}{2} \rho S_w V^2.\label{eq7.3.40}\]
   Також добре відомо, що коефіцієнт опору може бути виражений у параболічній формі наступним чином:
   \[C_D = C_{D_0} + C_{D_i} C_L^2,\label{eq7.3.41}\]
   де \(C_{D_0}\)наводиться в заяві і\(C_{D_i} = \tfrac{1}{\pi A e}\). Збільшення можна\(A\) обчислити як\(A = \tfrac{b^2}{S_w} = 12.30\) і, отже,:\(C_{D_i} = 0.0287\).
   Відповідно до Рівняння (\(\ref{eq7.3.38}\)):\(L = 686000\ N\). Швидкість польоту може бути розрахована як\(V = M_{\infty} a = 206.5\ m/s\). Після отримання цих значень із значеннями щільності та мокрої поверхні та введення в Рівняння (\(\ref{eq7.3.39}\)), ми отримуємо це\(C_L = 0.68\).
   Зі значеннями\(C_L\), і\(C_{D_i}\)\(C_{D_0}\), входячи в Рівняння (\(\ref{eq7.3.41}\)), ми отримуємо це\(C_D = 0.0332\).
   Дивлячись зараз на Equation (\(\ref{eq7.3.37}\)\(\ref{eq7.3.40}\)) і використовуючи Equation (), ми можемо констатувати, що необхідна тяга така:
   \[T = C_D \dfrac{1}{2} \rho S_w V^2.\nonumber\]
   Оскільки всі значення відомі, необхідна тяга дає:
   \[T = 33567\ N.\nonumber\]
   Перш ніж рухатися далі, слід подивитися, перевищує необхідну тягу чи ні максимальну доступну тягу на заданій висоті. Для цього було дано, що максимальна тяга змінюється лише з висотою наступним чином:
   \[T_{\max, av} (h) = T_{\max, av} (h = 0) \dfrac{\rho}{\rho_0}.\]
   Максимально доступна тяга при\(h = 11000\) врожайності:
   \[T_{\max, av} (h = 11000) = 35657.14\ N.\label{eq7.3.43}\]
   Оскільки\(T < T_{\max, av}\) політ стан літаючий.
2. Максимальна швидкість, обумовлена силовими обмеженнями літака і відповідним числом Маха, є горизонтальним, стійким, прямим
   польотом при\(h = 11000\): Максимальна швидкість через обмеження руху на заданій висоті передбачає політ з максимально доступною тягою що було отримано в Equation (\(\ref{eq7.3.43}\)).
   Подивившись знову на Equation (\(\ref{eq7.3.37}\)) і використовуючи Equation (\(\ref{eq7.3.40}\)), ми можемо стверджувати, що:
   \[T_{\max, av} = C_D \dfrac{1}{2} \rho S_w V^2.\label{eq7.3.44}\]
   Використовуючи рівняння (\(\ref{eq7.3.41}\)) і Рівняння (\(\ref{eq7.3.39}\)), і ввівши в Equation (\(\ref{eq7.3.44}\)) ми маємо що:
   \[T_{\max, av} = \left ( C_{D_0} + C_{D_i} \left (\dfrac{L}{\tfrac{1}{2} \rho S_w V^2} \right )^2 \right ) \dfrac{1}{2} \rho S_w V^2.\label{eq7.3.45}\]
   Помноживши Рівняння (\(\ref{eq7.3.45}\)) на\(V^2\) отримаємо квадратне рівняння виду:
   \[ax^2 + bx + c = 0.\]
   де\(x = V^2\),\(a = \tfrac{1}{2} \rho S_w C_{D_0}\),\(b = -T_{\max, av}\), і\(c = \dfrac{C_{D_i} L^2}{\tfrac{1}{2} \rho S_w}\).
   Вирішуючи квадратне рівняння, отримаємо дві різні швидкості, при яких літак може літати з урахуванням максимально доступної тяги ¹⁰. Ці швидкості дають:
   \[V_1 = 228\ m/s;\nonumber\]
   \[V_2 = 151\ m/s.\nonumber\]
   Максимальна відповідає, очевидно, до\(V_1\).
3. Мінімальна швидкість обумовлена аеродинамічними обмеженнями (стійла швидкість) при горизонтальному, стійкому, прямому польоті на всій висоті\(h = 11000\).
   Швидкість стійла відбувається, коли коефіцієнт підйому максимальний, тому, використовуючи Equation (\(\ref{eq7.3.39}\)), ми маємо що:
   \[V_{stall} = \sqrt{\dfrac{L}{\tfrac{1}{2} \rho S_w C_{L_{\max}}}} = 139\ m/s.\nonumber\]
4. Теоретичний стелю (максимальна висота) в горизонтальному, стійкому, прямому польоті.
   Для того, щоб отримати теоретичну стелю літака, максимальна доступна тяга на цій максимальній висоті повинна збігатися з мінімальною необхідною тягою для польоту горизонтального, стійкого, прямого польоту на цій максимальній висоті, тобто:
   \[T_{\max, av} = T_{\min}.\label{eq7.3.47}\]
   Давайте спочатку отримаємо мінімально необхідну тягу для польоту горизонтального, стійкого, прямого польоту. Помноживши і діливши на\(L\) у другому семестрі Рівняння (\(\ref{eq7.3.37}\)), і враховуючи, що аеродинамічна ефективність є\(E = \tfrac{L}{D}\), ми маємо що:
   \[T = \dfrac{D}{L} L = \dfrac{L}{E}.\]
   Оскільки\(L\) постійна при тих умовах польоту, виникає мінімальна необхідна тяга коли ККД максимальний:\(T_{\min} \Leftrightarrow E_{\max}\).
   Давайте тепер продовжимо виведення максимальної аеродинамічної ефективності:
   Аеродинамічна ефективність визначається як:
   \[E = \dfrac{L}{D} = \dfrac{C_L}{C_D}.\label{eq7.3.49}\]
   Підстановка параболічної полярної кривої, наведеної в Рівняння (\(\ref{eq7.3.41}\)) в Рівняння (\(\ref{eq7.3.49}\)) , отримуємо: Для
   \[E = \dfrac{C_L}{C_{D_0} + C_{D_i} C_L^2}.\label{eq7.3.50}\]
   того, щоб шукати значення, відповідні максимальному аеродинамічному ККД, треба вивести і зробити його рівним нулю, тобто:
   \[\dfrac{dE}{dC_L} = 0 \dfrac{C_{D_0} - C_{D_i} C_L^2}{(C_{D_0} + C_{D_i} C_L^2)^2} \to (C_L)_{E_{\max}} = C_{L_{opt}} = \sqrt{\dfrac{C_{D_0}}{C_{D_i}}}.\label{eq7.3.51}\]
   Підставляючи значення\(C_{L_{opt}}\) в Рівняння (\(\ref{eq7.3.50}\)) і спрощення отримаємо, що:
   \[E_{\max} = \dfrac{1}{2\sqrt{C_{D_0} C_{D_i}}}.\nonumber\]
   \(E_{\max}\) дає 20.86, і\(T_{\min} = 32870\ N\).
   Відповідно до Рівняння (\(\ref{eq7.3.43}\)) і на основі Equation (\(\ref{eq7.3.47}\)) з\(T_{\min} = 32870\ N\), ми маємо це:
   \[32870 = T_{\max, av} (h = 0) \dfrac{\rho}{\rho_0}.\nonumber\]
   Враховуючи, що\(T_{\max, av} (h = 0)\) було дано в твердженні і\(\rho_0\) відомо відповідно\(ISA\), ми маємо це \(\rho = 0.335\ kg/m^3\).
   Так як\(\rho_{h_{\max}} < \rho_{11000}\) ми можемо легко зробити висновок, що ейлінг належить до стратосфери. Використовуючи\(ISA\) рівняння, відповідне стратосфері, ми маємо
   \[\rho_{h_{\max}} = \rho_{11} \exp^{-\tfrac{g}{TR_{11}} (h_{\max} - h_{11})}.\label{eq7.3.52}\]
   таке: де підіндекс 11 відповідає значенням на тропопаузі\((h = 11000\ m)\). Працюючи в Equation (\(\ref{eq7.3.52}\)), стеля виходить\(h_{\max} = 11526\ m\).
5. Необхідний кут берега:
   Рівняння, що регулюють динаміку літака в горизонтальному повороті, є:
   \[T = D;\label{eq7.3.53}\]
   \[m V \dot{\chi} = L \sin \mu;\label{eq7.3.54}\]
   \[L \cos \mu = mg.\label{eq7.3.55}\]
   У рівномірному (нерухомому) круговому русі, добре відомо, що тангенціальна швидкість дорівнює кутовій швидкості (\(\dot{\chi}\)), помноженої на радіус повороту (\(R\)):
   \[V = \dot{\chi} R.\]
   Тому System (\(\ref{eq7.3.53}\),\(\ref{eq7.3.54}\) і\(\ref{eq7.3.55}\)) можна переписати як:
   \[T = D;\label{eq7.3.57}\]
   \[n \sin \mu = \dfrac{V^2}{gR};\label{eq7.3.58}\]
   \[n = \dfrac{1}{\cos \mu};\label{eq7.3.59}\]
   де\(n = \tfrac{L}{mg}\) - коефіцієнт навантаження.
   Тому, дивлячись на Equation (\(\ref{eq7.3.59}\)), нескладно визначити, що кут повороту банку є\(\mu = 60^{\circ}\).
6. Радіус повороту.
   Для початку потрібно розрахувати швидкість, відповідну максимальному ККД. Як ми розраховували раніше в Equation (\(\ref{eq7.3.51}\)), коефіцієнт підйому, який генерує максимальну ефективність, є так званим оптимальним коефіцієнтом підйому, тобто\(C_{L_{opt}} = \sqrt{\dfrac{C_{D_0}}{C_{D_i}}} = 0.834\). Швидкість виходить тоді:
   \[V = \sqrt{\dfrac{L}{\tfrac{1}{2} \rho S_w C_{L_{opt}}}} = 186.4\ m/s.\nonumber\]
   Введення рівняння (\(\ref{eq7.3.58}\)) з\(\mu = 60\ [deg]\) і\(V = 186.4\ m/s\);\(R = 4093.8\ m\).
7. Необхідна тяга.
   Як виставляється в питанні 3, Рівняння (\(\ref{eq7.3.57}\)) можна виразити
   \[T = \dfrac{1}{2} \rho S_w V^2 C_{D_0} + \dfrac{L^2}{\tfrac{1}{2} \rho V^2 S_w} C_{D_i}.\nonumber\]
   так:\(T = 32451\ N\)
   Оскільки всі значення відомі: Оскільки\(T \le T_{\max, av} (h = 110000)\) літак може виконувати поворот.
8. Ми хочемо виконати горизонтальний поворот з тим же коефіцієнтом навантаження і тим же радіусом, що і попередній випадок, але на висоті, відповідній театральному стелі літака. Чи може літак виконати поворот?
   Якщо коефіцієнт навантаження однаковий\(n = 2\), обов'язково (відповідно до Рівняння (\(\ref{eq7.3.59}\)) кут банку однаковий,\(\mu = 60^{\circ}\). Також, якщо радіус повороту однаковий\(R = 4093.8\ m\), обов'язково (згідно з Equation (\(\ref{eq7.3.58}\)), швидкість повороту повинна бути такою ж, як і в попередньому випадку\(V = 186.4\ m/s\). Очевидно, що оскільки щільність буде змінюватися відповідно до нової висоти (\(\rho = 0.335\ kg/m^3\)), поворот не буде виконуватися в умовах максимальної ефективності.
   Для того щоб знати, чи можна виконати поворот чи ні, ми повинні порівняти необхідну тягу з максимально доступною тягою на висоті стелі:
   \[T = \dfrac{1}{2} \rho S_w V^2 C_{D_0} + \dfrac{L^2}{\tfrac{1}{2} \rho V^2 S_w} C_{D_i} = 32983\ N.\nonumber\]
   \[T_{\max, av} (h = 11526) = T_{\max, av} (h = 0) \dfrac{\rho}{\rho_0} = 32816\ N.\nonumber\]
   Так як\(T > T_{\max, av}\) на стелі поворот виконувати не можна.

Вправа\(\PageIndex{4}\) Weights

Розглянемо Airbus А-320. Спрощуючи, ми припускаємо, що крило літака є прямокутником, і воно складається на аеродромах NACA 4415. Характеристики аеродропласту NACA 4415 наступні:

• \(c_l = 0.2 + 5.92 \alpha\). (\(\alpha\)в радіанах).
• \(c_d = 6.4 \cdot 10^{-3} - 1.2 \cdot 10^{-3} c_l + 3.5 \cdot 10^{-3} c_l^2\).

Щодо літака відомі наступні дані:

• Крило мокра поверхня 122,6\([m^2]\).
• Розмах крила 34.1\([m]\).
• Коефіцієнт корисної дії Освальда 0,95.
• Питома витрата на одиницю тяги і часу:\(\eta_j = 6.8 \cdot 10^{-5} [\tfrac{Kg}{N \cdot s}]\).

Обчисліть:

1. Підйом крила в його лінійному діапазоні.
2. Полярна крива перетягування, припускаючи, що вона може бути виражена у вигляді:\(C_D = C_{D_0} + C_{D_i} C_L^2\).
3. Оптимальний коефіцієнт підйому крила,\(C_{L_{opt}}\). Порівняйте його з аерофолистом.

Щодо характерних ваг літака відомі наступні дані:

• Експлуатаційна порожня маса\(OEW = 42.4\ [Ton]\).
• Максимальна злітна маса\(MTOW = 77000 \cdot g\ [N]\) ¹¹.
• Максимальна маса палива\(MFW = 29680 \cdot g\ [N]\).
• Максимальна нульова маса палива\(MZFW = 59000 \cdot g\ [N]\).
• Крім того, резервне паливо (\(RF\)) можна розрахувати як 5% від Trip Fuel (\(TF\)).

Обчисліть:

4. Корисне навантаження і відключення палива в наступних випадках:

(a) Початкова вага дорівнює\(MTOW\) максимальному корисному навантаженню\((MPL)\).
(b) Початкова вага дорівнює\(MTOW\) максимальній масі палива\((MFW)\).
(c) Початкова вага дорівнює\(OEW\) плюс\(MFW\).

Припускаючи, що в умовах круїзу літак летить на постійній висоті\(h = 11500\ [m]\), постійному\(M = 0.78\) числі Маха і максимальному аеродинамічному ККД, враховуючи\(ISA\) стандартну атмосферу, обчислюють:

5. Дальність і автономність літака для трьох початкових ваг, зазначених вище.

6. За отриманими результатами намалюйте діаграму корисного навантаження.

Відповідь

1. Крива підйому крила:
   Крива підйому крила може бути виражена наступним чином:
   \[C_L = C_{L_0} + C_{L_{\alpha}} \alpha,\label{eq7.3.60}\]
   і нахил кривої підйому крила може бути виражений, пов'язаний з нахилом кривої підйому аеропрофілю як:
   \[C_{L_{\alpha}} = \dfrac{C_{l_{\alpha}}}{1 + \tfrac{C_{l_{\alpha}}}{\pi A}} e = 4.69 \cdot 1/rad.\nonumber\]
   Для того щоб обчислити незалежний термін кривої підйому крила, ми повинні враховувати той факт, що нульовий кут атаки крила збігається з нульовим кутом підйому атаки аеропрофілю, тобто:
   \[\alpha (L = 0) = \alpha (l = 0).\label{eq7.3.61}\]
   По-перше, зверніть увагу, що крива підйому аерокрила може бути виражена наступним чином
   \[C_l = C_{l_0} + C_{l_{\alpha}} \alpha.\label{eq7.3.62}\]
   Отже, за допомогою Equation (\(\ref{eq7.3.60}\)) та Equation (\(\ref{eq7.3.61}\)) у Рівняння (\(\ref{eq7.3.62}\)) ми маємо це:
   \[C_{L_0} = C_{l_0} \dfrac{C_{L_{\alpha}}}{C_{l_{\alpha}}} = 0.158.\nonumber\]
   Необхідна крива дає потім:
   \[C_L = 0.158 + 4.69 \alpha \ [\alpha \ in\ rad].\nonumber\]
2. Вираз параболічного полярного крила:
   Зверніть увагу спочатку, що постановка задачі вказує на те, що полярний повинен бути в наступному вигляді:
   \[C_D = C_{D_0} + C_{D_i} C_L^2.\label{eq7.3.63}\]
   Для розрахунку параболічного опору крила ми можемо вважати термін паразита приблизно рівним терміном паразита аерофольга, тобто\(C_{D_0} = C_{d_0}\).
   Індукований коефіцієнт опору можна обчислити наступним чином:
   \[C_{D_i} = \dfrac{1}{\pi Ae} = 0.035.\nonumber\]
   Вираз параболічного полярного дає тоді:
   \[C_D = 0.0064 + 0.035 C_L^2.\]
3. Оптимальний коефіцієнт підйому\(C_{L_{opt}}\),, для крила. Порівняйте його з аеропрофілями.
   Оптимальним коефіцієнтом підйому є те, що робить аеродинамічний ККД максимальним. Аеродинамічна ефективність визначається як:
   \[E = \dfrac{L}{D} = \dfrac{C_L}{C_D}.\label{eq7.3.65}\]
   Підставляючи параболічну полярну криву, задану в Рівнянні (\(\ref{eq7.3.65}\)) у Рівнянні (), отримуємо:
   \[E = \dfrac{C_L}{C_{D_0} + C_{D_i} C_L^2}.\label{eq7.3.66}\]
   Для пошуку значень, відповідних\(\ref{eq7.3.63}\) максимальний аеродинамічний ККД, потрібно вивести і зробити його рівним нулю, тобто:
   \[\dfrac{dE}{dC_L} = 0 = \dfrac{C_{D_0} - C_{D_i} C_L^2}{(C_{D_0} - C_{D_i} C_L^2)^2} \to (C_L)_{E_{\max}} = C_{L_{opt}} = \sqrt{\dfrac{C_{D_0}}{C_{D_i}}}.\label{eq7.3.67}\]
   Для випадку аеродинамічного ККД визначається як:
   \[E = \dfrac{l}{d} = \dfrac{c_l}{c_d}.\label{eq7.3.68}\]
   Заміна параболічного полярного криву, наведену в твердженні\(c_{d_0} + bc_l + kc_l^2\) у вигляді в Equation (\(\ref{eq7.3.68}\)), отримаємо:
   \[E = \dfrac{c_l}{c_{d_0} + bc_l + kc_l^2}.\]
   Для того щоб шукати значення, відповідні максимальному аеродинамічному ККД, треба вивести і зробити його рівним нулю, тобто:
   \[\dfrac{dE}{dC_l} = 0 = \dfrac{c_{d_0} - kc_l^2}{(c_{d_0} + bc_l + kc_l^2)^2} \to (c_l)_{E_{\max}} = (c_l)_{opt} = \sqrt{\dfrac{c_{d_0}}{k}}.\label{eq7.3.70}\]
   За раніше отриманими значеннями (\(C_{D_0} = 0.0064\)і\(C_{D_i} = 0.035\)) і значеннями, наведеними в заяві для полярного (\(c_{d_0} = 0.0064\),\(k = 0.0035\)) аерофольга, підставляючи їх відповідно в Equation (\(\ref{eq7.3.67}\)\(\ref{eq7.3.70}\)) і Equation () отримуємо:
   \(\bullet\)\((C_L)_{opt} = 0.42;\)
   \(\bullet\)\((c_l)_{opt} = 1.35.\)
4. Корисне навантаження та відключення палива для випадку (a), (b) та (c):
   Перед запуском ми конкретні випадки, необхідно зазначити, що:
   \[TOW = OEW + PL + FW,\label{eq7.3.71}\]
   \[FW = TF + RF,\label{eq7.3.72}\]
   \[MZFW = OEW + MPL.\label{eq7.3.73}\]
   Крім того, відповідно до твердження,
   \[RF = 0.05 \cdot TF.\]
   засноване на даних, наведених у твердженні, і за допомогою Рівняння (\(\ref{eq7.3.73}\)):
   \[MPL = 16.6\ [Ton.].\]
   Випадок (а) Початкова вага ¹²\(\to\)\(MTOW\) с\(MPL\).
   Рівняння (\(\ref{eq7.3.71}\)) стає:
   \[MTOW = OEW + MPL + TF + 0.05 \cdot TF,\label{eq7.3.76}\]
   Ізоляція в рівнянні (\(\ref{eq7.3.76}\)):\(TF = 17.14\ [Ton]\). Корисне навантаження дорівнює максимальному корисному навантаженню\(MPL\).
   Випадок (б) Початкова вага\(\to\)\(MTOW\) с\(MFW\).
   Рівняння (\(\ref{eq7.3.71}\)) стає:
   \[MTOW = OEW + PL + MFW,\label{eq7.3.77}\]
   Ізоляція в рівнянні (\(\ref{eq7.3.77}\)):\(PL = 4.92\ [Ton]\). Для того, щоб розрахувати відключення палива, дивлячись на Рівняння (\(\ref{eq7.3.72}\)), ми маємо, що
   \[MFW = TF + RF = TF + 0.05 \cdot TF.\]
   Ізоляція,\(TF = 28.266\ [Ton.]\).
   Випадок (c) Початкова вага\(\to\)\(OEW + MFW\).
   Рівняння (\(\ref{eq7.3.71}\)) стає: Це означає\(PL = 0\),
   \[TOW = OEW + MFW,\]
   що для того, щоб розрахувати відключення палива, ми діємо точно так, як у випадку (b). Дивлячись на рівняння (\(\ref{eq7.3.72}\)), ми маємо, що
   \[MFW = TF + RF = TF + 0.05 \cdot TF.\]
   Ізоляція,\(TF = 28.266\ [Ton.]\)
5. Дальність і витривалість для випадків (a), (b) і (c): Враховуючи, що літак виконує лінійний, горизонтальний стійкий політ, ми маємо, що:
   \[L = mg;\label{eq7.3.81}\]
   \[T = D;\label{eq7.3.82}\]
   \[\dot{x} = V;\label{eq7.3.83}\]
   \[\dot{m} = -\eta T.\label{eq7.3.84}\]
   Оскільки\(\dot{x} = \tfrac{dx}{dt}\), зрозуміло, що Діапазон\(R\), дивлячись на Рівняння (\(\ref{eq7.3.83}\)), може бути виражений так:
   \[R = \int_{t_i}^{t_f} V dt.\label{eq7.3.85}\]
   Тепер, оскільки\(\dot{m} = \tfrac{dm}{dt} = -\eta T\), Рівняння (\(\ref{eq7.3.85}\)):
   \[R = \int_{m_i}^{m_f} -\dfrac{V}{\eta T} dm,\label{eq7.3.86}\]
   де\(m_i\) початкова маса і\(m_f\) є кінцевою масою.
   Використовуючи Рівняння (\(\ref{eq7.3.81}\)) та Рівняння (\(\ref{eq7.3.82}\)), Рівняння (\(\ref{eq7.3.86}\)) дає:
   \[R = \int_{m_i}^{m_f} - \dfrac{VE}{\eta g} \dfrac{dm}{m}.\]
   з\(E = \tfrac{L}{D}, V, \eta\), і\(g\) є постійними значеннями.
   Інтеграція:
   \[R = \dfrac{VE}{\eta g} \ln (\dfrac{m_i}{m_f}).\label{eq7.3.88}\]
   Для витривалості ми працюємо аналогічно, інтегруючи рівняння (\(\ref{eq7.3.84}\)), яке дає
   \[t = \int_{m_i}^{m_f} - \dfrac{1}{\eta T} dm.\label{eq7.3.89}\]
   Використання рівняння (\(\ref{eq7.3.81}\)) та (\(\ref{eq7.3.82}\)), ( \(\ref{eq7.3.89}\)) прибутковість:
   \[t = \int_{m_i}^{m_f} - \dfrac{E}{\eta g} \dfrac{dm}{m}.\]
   де знову\(E = \tfrac{L}{D}\),\(\eta\) і\(g\) є постійними значеннями. Інтеграція:
   \[t = \dfrac{E}{\eta g} \ln (\dfrac{m_i}{m_f}).\label{eq7.3.91}\]
   Перед розрахунком діапазону та витривалості для трьох випадків нам потрібно обчислити значення швидкості та аеродинамічної ефективності, яка є максимальною.
   Швидкість може бути виражена як\(V = M \cdot a\), де\(a\) швидкість звуку, що може бути виражено як
   \[a = \sqrt{\gamma RT},\]
   де\(\gamma = 1.4\) адіабатичний коефіцієнт повітря, і\(R = 287\ J/KgK\) є ідеальною газовою константою. Зверніть увагу, що\(ISA\), використовуючи, температура в стратосфері постійна, і, таким чином\(T = 216.6\ K\).
   Підставляючи всі терміни, вона поступається\(v = 230.1\ [m/s]\).
   Аеродинамічний ККД максимальний. Таким чином, підставляючи\(C_{L_{opt}}\) отримані в Equation (\(\ref{eq7.3.66}\)) на Equation (), він дає:
   \[E = \dfrac{1}{2\sqrt{C_{D_0} C_{D_i}}} = 33.4.\]
   Тепер ми повинні обчислити початкову та кінцеву масу для трьох випадків a), b), c).\(\ref{eq7.3.67}\) Зверніть увагу, що кінцева маса є результатом віднімання палива відключення з злітної маси:
   \[m_f = m_i - TF.\]
   Таким чином,
   (а)\(m_i = \dfrac{MTOW}{g} [Kg]\) і\(m_f = 59860\ [Kg]\).
   (б)\(m_i = \dfrac{MTOW}{g} [Kg]\) і\(m_f = 48734\ [Kg]\).
   (в)\(m_i = 72080 [Kg]\) і\(m_f = 43814\ [Kg]\).
   Підставляючи в Рівняння (\(\ref{eq7.3.88}\)) і Рівняння (\(\ref{eq7.3.91}\)), він дає:
   (а)\(R_a = 2900\ [Km]\) і\(t_a = 12600\ [s]\).
   (б)\(R_b = 5270\ [Km]\) і\(t_b = 22900\ [s]\).
   (в)\(R_c = 5736\ [Km]\) і\(t_c = 24928\ [s]\).
6. Випадки діаграми діапазону корисного навантаження (a), (b) та (c):
   
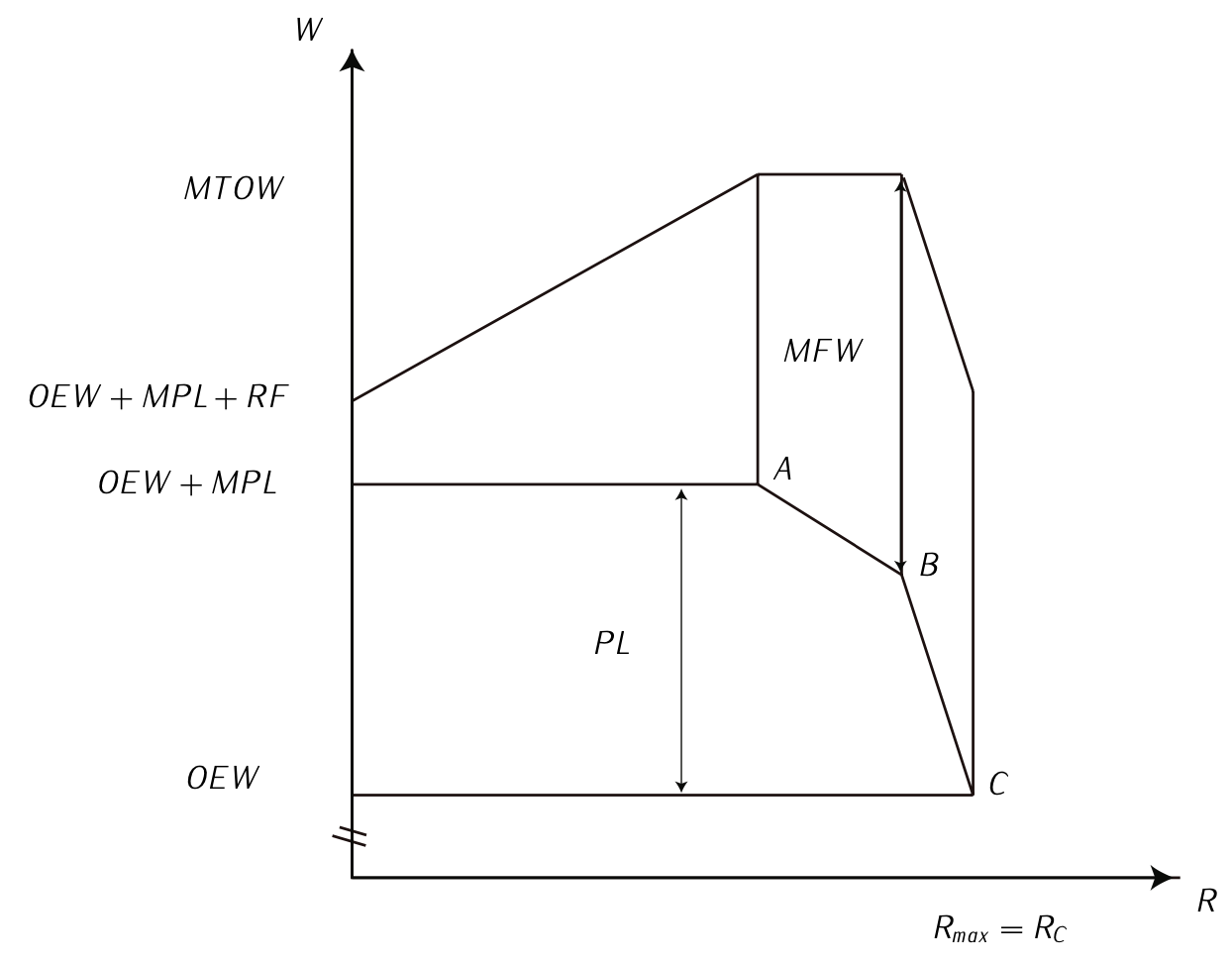
   Рисунок 7.17: Діаграма корисного навантаження

Вправа\(\PageIndex{5}\)

Літак має такі характеристики:

• \(S_w = 130\ m^2\).
• \(b = 40\ m\).
• \(m = 70000\ kg\).
• \(T_{\max, av, 0} = 130000\ N\)(Максимально доступна тяга на рівні моря).
• \(C_{D_0} = 0.02\).
• Коефіцієнт корисної дії Освальда:\(e = 0.9\).

Максимально доступну тягу можна вважати варіюватися відповідно до наступного закону:

\[T_{\max, av} (h) = T_{\max, av, 0} \dfrac{\rho}{\rho_0}.\nonumber\]

Враховуйте\(ISA\) атмосферу і постійну гравітацію\(g = 9.8\ m/s^2\). Визначте:

1. Необхідна тяга для польоту на висоті\(h = 11250\ m\) при\(M_{\infty} = 0.78\) стійкому лінійно-горизонтальному польоті.
2. Максимальна швидкість літака обумовлена силовими обмеженнями при стійкому лінійно-горизонтальному польоті на висоті\(h = 11250\ m\).
3. Теоретична стеля літака в стійкому лінійно-горизонтальному польоті.

Тепер ми хочемо визначити поверхню горизонтального стабілізатора і в якості конструктивного критерію візьмемо умови польоту рівноваги на висоті\(h = 11250\ m\) &\(M_{\infty} = 0.78\). У тих умовах коефіцієнт підйому стабілізатора дорівнює 1,4. Більш того, можна припустити, що розподіл підйому крила може бути зведений до результуючої сили в аеродинамічному центрі (підйомі) і качального моменту вниз по відношенню до аеродинамічного центру рівному\(10000\ N \cdot m\). Відстань між аеродинамічним центром і центром ваги (зверніть увагу, що аеродинамічний центр знаходиться ближче до носа літака) становить\(x_{cg} = 2\ m\). Відстань між стабілізатором і центром ваги дорівнює\(l = 20\ m\).

4. Визначте поверхню горизонтального стабілізатора для тих умов польоту.

Відповідь

Крім даних, наведених у заяві, були використані наступні дані:

• \(R = 287\ J/(kgK)\).
• \(\gamma_{air} = 1.4\).
• \(T_{11} = 216.6\ K\).
• \(\rho_{11} = 0.36\ kg/m^3\).
• \(T_0 = 288.15\ K\).
• \(ISA: \rho = \rho_{11} \cdot e^{\tfrac{-gR}{T_{11}}} (h - 11000)\).

1. Необхідна тяга для польоту горизонтального, стійкого, прямого польоту при наступних умовах польоту:
   \(\bullet\)\(h = 11.250\ m\).
   \(\bullet\)\(M_{\infty} = 0.78\).
   За словами\(ISA\):
   \(\bullet\)\(\rho (h = 11250) = 0.3461\ Kg/m^3\).
   \(\bullet\)\(a (h = 11250) = \sqrt{\gamma_{air} R(T_{11})} = 295\ m/s\).
   де a відповідає швидкості звуку.
   Система, яка керує динамікою літака, є:
   \[T = D,\label{eq7.3.95}\]
   \[L = mg,\label{eq7.3.96}\]
   бути\(L\) підйомом,\(mg\) вагою;\(T\) довірою та\(D\) перетягуванням.
   Добре відомо, що:
   \[L = C_L \dfrac{1}{2} \rho S_w V^2;\label{eq7.3.97}\]
   \[D = C_D \dfrac{1}{2} \rho S_w V^2.\label{eq7.3.98}\]
   Також добре відомо, що коефіцієнт опору може бути виражений у праболічній формі наступним чином:
   \[C_D = C_{D_0} + C_{D_i} C_L^2,\label{eq7.3.99}\]
   де \(C_{D_0}\)наводиться в заяві і\(C_{D_i} = \tfrac{1}{\pi Ae}\). Збільшення\(A\) може бути розраховане як\(A = \tfrac{b^2}{S_w} = 12.30\) і, отже,:\(C_{D_i} = 0.0287\).
   Відповідно до Рівняння (\(\ref{eq7.3.96}\)):\(L = 686000\ N\). Швидкість польоту може бути розрахована як\(V = M_{\infty} a = 230.1\ m/s\). Після отримання цих значень із значеннями щільності та мокрої поверхні та введення в Рівняння (\(\ref{eq7.3.97}\)), ми отримуємо це\(C_L = 0.5795\).
   За допомогою значень\(C_L, C_{D_i}\) і\(C_{D_0}\), входячи в Рівняння (\(\ref{eq7.3.99}\)), ми отримуємо це\(C_D = 0.0295\).
   Дивлячись зараз на Equation (\(\ref{eq7.3.95}\)\(\ref{eq7.3.98}\)) і використовуючи Equation (), ми можемо констатувати, що необхідна тяга така:
   \[T = C_D \dfrac{1}{2} \rho S_w V^2.\nonumber\]
   Оскільки всі значення відомі, необхідна тяга дає:
   \[T = 35185\ N.\nonumber\]
   Перш ніж рухатися далі, слід подивитися, перевищує необхідну тягу чи ні максимальну доступну тягу на заданій висоті. Для цього було дано, що максимальна тяга змінюється лише з висотою наступним чином:
   \[T_{\max, av} (h) = T_{\max, av, 0} \dfrac{\rho}{\rho_0}.\label{eq7.3.100}\]
   Максимально доступна тяга при\(h = 11250\) врожайності:
   \[T_{\max, av} (h = 11250) = 36729\ N.\label{eq7.3.101}\]
   Оскільки\(T < T_{\max, av}\) політ стан літаючий.
2. Максимальна швидкість, обумовлена рухливими обмеженнями літака в горизонтальному, стійкому, прямому польоті при\(h = 11250\):
   Максимальна швидкість через обмеження руху на заданій висоті передбачає політ з максимально доступною тягою, яка була отримана в Рівнянні ( \(\ref{eq7.3.101}\)).
   Подивившись знову на рівняння (\(\ref{eq7.3.95}\)) і використовуючи Equation (\(\ref{eq7.3.98}\)), ми можемо стверджувати, що:
   \[T_{\max, av} = C_D \dfrac{1}{2} \rho S_w V^2.\label{eq7.3.102}\]
   Використовуючи рівняння (\(\ref{eq7.3.99}\)) і Рівняння (\(\ref{eq7.3.97}\)), і ввівши в Equation (\(\ref{eq7.3.102}\)) ми маємо що:
   \[T_{\max, av} = \left (C_{D_0} + C_{D_i} \left (\dfrac{L}{\tfrac{1}{2} \rho S_w V^2} \right )^2 \right ) \dfrac{1}{2} \rho S_w V^2.\label{eq7.3.103}\]
   Помноживши Рівняння (\(\ref{eq7.3.103}\)) на\(V^2\) отримаємо квадратне рівняння виду:
   \[ax^2 + bx + c = 0.\]
   де\(x = V^2\),\(a = \dfrac{1}{2} \rho S_w C_{D_0}, b = - T_{\max, av}\) і\(c = \dfrac{C_{D_i} L^2}{\tfrac{1}{2} \rho S_w}\).
   Вирішуючи квадратне рівняння, отримаємо дві різні швидкості, з якими літак може літати, враховуючи максимально доступну тягу13. Ці швидкості дають:
   \[V_1 = 218\ m/s;\nonumber\]
   \[V_2 = 184.06\ m/s.\nonumber\]
   Максимальна швидкість відповідає, очевидно,\(V_1\).
3. Теоретичний стелю (максимальна висота) в горизонтальному, стійкому, прямому польоті.
   Для того, щоб отримати теоретичну стелю літака, максимальна доступна тяга на цій максимальній висоті повинна збігатися з мінімальною необхідною тягою для польоту горизонтального, стійкого, прямого польоту на цій максимальній висоті, тобто:
   \[T_{\max, av} = T_{\min}.\label{eq7.3.105}\]
   Давайте спочатку отримаємо мінімально необхідну тягу для польоту горизонтального, стійкого, прямого польоту. Множивши та діливши на\(L\) у другому семестрі Рівняння (\(\ref{eq7.3.95}\)), і враховуючи, що ефективність аеродинаміки є\(E = \tfrac{L}{D}\), ми маємо що:
   \[T = \dfrac{D}{L} L = \dfrac{L}{E}.\]
   Оскільки\(L\) постійна при тих умовах польоту, виникає мінімальна необхідна тяга коли ККД максимальний:\(T_{\min} \Leftrightarrow E_{\max}\).
   Давайте тепер продовжимо виведення максимальної аеродинамічної ефективності:
   Аеродинамічна ефективність визначається як:
   \[E = \dfrac{L}{D} = \dfrac{C_L}{C_D}.\label{eq7.3.107}\]
   Заміна параболічної полярної кривої, наведеної в рівнянні полярної кривої, наведеної в Рівнянні ( \(\ref{eq7.3.99}\)) в Рівнянні (\(\ref{eq7.3.107}\)) отримуємо: Для
   \[E = \dfrac{C_L}{C_{D_0} + C_{D_i} C_L^2}.\label{eq7.3.108}\]
   того, щоб шукати значення, відповідні максимальному аеродинамічному ККД, потрібно вивести і зробити його рівним нулю, тобто:
   \[\dfrac{dE}{dC_L} = 0 = \dfrac{C_{D_0} - C_{D_i} C_L^2}{(C_{D_0} + C_{D_i} C_L^2)^2} \to (C_L)_{E_{\max}} = C_{L_{opt}} = \sqrt{\dfrac{C_{D_0}}{C_{D_i}}}.\]
   Підставляючи значення\(C_{L_{opt}}\) в Equation (\(\ref{eq7.3.108}\)) і спрощуючи, отримаємо, що:
   \[E_{\max} = \dfrac{1}{2\sqrt{C_{D_0} C_{D_i}}}.\nonumber\]
   \(E_{\max}\) дає 20.86, і\(T_{\min} = 32904\ N\).
   Відповідно до Рівняння (\(\ref{eq7.3.101}\)) і на основі Equation (\(\ref{eq7.3.105}\)) з\(T_{\min} = 32904\ N\), ми маємо це:
   \[32904 = T_{\max, av, 0} \dfrac{\rho}{\rho_0}.\nonumber\]
   Враховуючи, що\(T_{\max, av, 0}\) було дано в твердженні і\(\rho_0\) відомо відповідно\(ISA\), ми маємо це \(\rho = 0.3101\ kg/m^3\).
   Так як\(\rho_{h_{\max}} < \rho_{11000}\) ми легко можемо зробити висновок, що стеля відноситься до стратосфери. Використовуючи\(ISA\) рівняння, відповідне стратосфері, ми маємо
   \[\rho_{h_{\max}} = \rho_{11} \exp^{-\tfrac{g}{RT_{11}} (h_{\max} - h_{11})}.\label{eq7.3.110}\]
   таке: де підіндекс 11 відповідає значенням на тропопаузі\((h = 11000\ m)\). Працюючи в Equation (\(\ref{eq7.3.110}\)), стеля виходить\(h_{\max} = 11946\ m\).
4. Ми хочемо визначити поверхню горизонтального стабілізатора:
   Для цього ми встановлюємо рівняння для задачі поздовжнього балансування:
   \[mg - L - L_t = 0;\label{eq7.3.111}\]
   \[-M_{ca} + Lx_{cg} - L_t l = 0;\label{eq7.3.112}\]
   де\(L_t\) підйом генерується горизонтальним стабілізатором,\(M_{ca} = 10000\ Nm\) є кроком крутного моменту щодо аеродинамічного центру,\(x_{cg} = 2\ m\) це відстань між центром ваги та аеродинамічним центром, а\(l = 20\ m\) також відстань між центром ваги та аеродинамічним центром горизонталі стабілізатор.
   Увійшовши в рівняння (\(\ref{eq7.3.111}\)), ми маємо це\(L = mg - L_t\). Знаючи це\(L_t = 0.5 \rho S_t V^2 C_L\), і підставляючи в Equation (\(\ref{eq7.3.112}\)), ми маємо, що:
   \[L_t = \dfrac{mg \cdot x_{cg} - M_{ca}}{l + x_{cg}} \to S_t = \dfrac{1}{0.5 \rho V^2 C_{L_t}} \dfrac{mg \cdot x_{cg} - M_{ca}}{l + x_{cg}} = 4.78\ m^2.\]

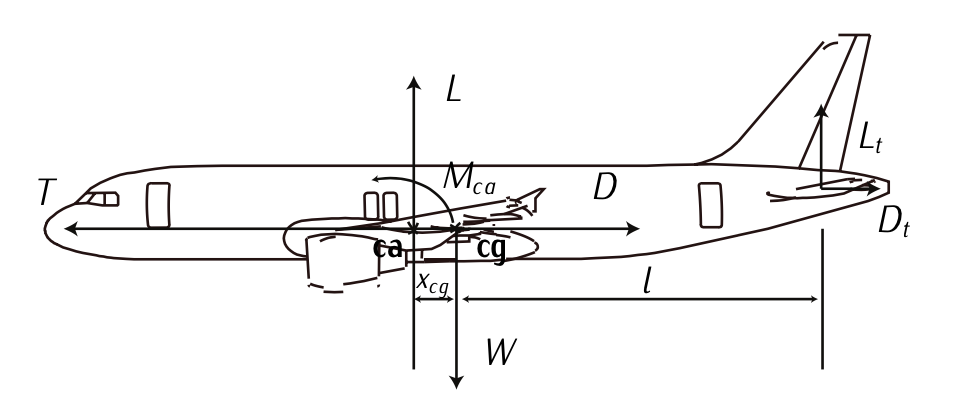
Малюнок 7.18: Поздовжня рівновага.

Вправа\(\PageIndex{6}\) Performances

Розглянемо Airbus A-320 з наступними характеристиками:

• \(m = 64\)тонн.
• \(S_w = 122.6\ m^2\)
• \(T_{\max, av, 0} = 130000\ N\)(Максимально доступна тяга на рівні моря).
• \(C_D = 0.024 + 0.0375 C_L^2\).

Максимально доступну тягу можна вважати варіюватися відповідно до наступного закону:

\[T_{\max, av} (h) = T_{\max, av, 0} \dfrac{\rho}{\rho_0}.\nonumber\]

Враховуйте\(ISA\) атмосферу і постійну гравітацію\(g = 9.8\ m/s^2\).

1. Літак починає рівномірний маневр підйому (постійна швидкість і кут шляху польоту) на висоті 10.000 футів (\(3048\ m\)). На цьому рівні польоту аеродинамічна швидкість є\(150\ m/s\) і вертикальна швидкість\(12\ m/s\). Припускаючи невеликий кут атаки\(\gamma \ll 1\), обчисліть:
   (а) кут траєкторії польоту підйому,\(\gamma\).
   (б) Необхідна тяга при цих умовах.
   (c) Відношення удару ¹⁴ щодо максимальної доступної тяги на цій висоті.
2. Обчисліть максимальний кут підйому (кут траєкторії польоту) при рівномірному підйомі на висоті 10000 футів. У цих умовах визначають:
   (а) аеродинамічну швидкість і вертикальну швидкість.
3. Хочемо зараз проаналізувати показники повороту в горизонтальній площині. Враховуйте умови рівня моря, максимальну аеродинамічну ефективність та структурні обмеження, що характеризуються максимальним коефіцієнтом навантаження\(n_{\max} = 2.5\). У цих умовах обчислити:
   (а) необхідний кут банку.
   (b) Швидкість і радіус повороту.
   (в) Необхідна тяга.
   (d) Чи може літак виконати повний поворот?

Відповідь

Крім даних, наведених у заяві, були використані наступні дані:

• \(g = 9.81\ m/s^2\).
• \(R = 287\ J/(kgK)\).
• \(\alpha_T = 6.5 \cdot 10^{-3}\ K/m\).
• \(\rho_0 = 1.225\ kg/m^3\).
• \(T_0 = 288.15\ K\).
• \(ISA: \rho = \rho_0 (1 - \dfrac{\alpha_T h}{T_0})^{\tfrac{gR}{\alpha_T} - 1}\).

1. Рівномірно-підйом при наступних умовах польоту:
   \(\bullet\)\(h = 3048\ m\). Використання\(ISA \to \rho = 0.904\ kg/m^3\).
   \(\bullet\)\(V = 150\ m/s\).
   \(\bullet\)\(\dot{h}_e = 12\ m/s\).
   Система, яка керує рухом літака:
   \[T = D + mg \sin \gamma;\label{eq7.3.114}\]
   \[L = mg \cos \gamma;\label{eq7.3.115}\]
   \[\dot{x}_e = V \cos \gamma;\label{eq7.3.116}\]
   \[\dot{h}_e = V \sin \gamma.\label{eq7.3.117}\]
   Припускаючи\(\gamma \ll 1\), що, і, таким чином, що\(\cos \gamma \sim 1\) і \(\sin \gamma \sim \gamma\), Система (\(\ref{eq7.3.114}\),,\(\ref{eq7.3.115}\)\(\ref{eq7.3.116}\),\(\ref{eq7.3.117}\)) стає:
   \[T = D + mg \gamma;\label{eq7.3.118}\]
   \[L = mg;\label{eq7.3.119}\]
   \[\dot{x}_e = V;\label{eq7.3.120}\]
   \[\dot{h}_e = V_{\gamma}. \label{eq7.3.121}\]
   (а) З рівняння\(\ref{eq7.3.121}\),\(\gamma = \tfrac{\dot{h}_e}{V} = 0.08\ rad (4.58^{\circ})\).
   (б) З рівняння\(\ref{eq7.3.118}\),\(T = D + mg\gamma\).
   \[D = C_D \dfrac{1}{2} \rho S_w V^2,\label{eq7.3.122}\]
   де\(C_D = 0.024 + 0.0375 C_L^2\), і\(\rho, S_w, V^2\) відомі.
   \[C_L = \dfrac{L}{\tfrac{1}{2} \rho S_w V^2} = 0.5057.\label{eq7.3.123}\]
   де, згідно з рівнянням (\(\ref{eq7.3.119}\)),\(L = mg\). З рівнянням (\(\ref{eq7.3.123}\)) в рівнянні (\(\ref{eq7.3.122}\)),\(D = 41398\ N\).
   Нарешті:
   \[T = D + mg \gamma = 91886\ N.\nonumber\]
   (c) Максимальна тяга в цих умовах є
   \[T_{\max, av} (h = 3048) = T_{\max, av, 0} \dfrac{\rho}{\rho_0} = 95510\ N.\nonumber\]
   Співвідношення є\(\sqcap = \tfrac{T}{T_{\max, av}} = 0.962\).
2. Максимальний кут підйому.
   Розглядаємо знову безліч рівнянь (\(\ref{eq7.3.118}\),\(\ref{eq7.3.119}\),\(\ref{eq7.3.120}\),\(\ref{eq7.3.121}\)). Рівняння дайвінгу (\(\ref{eq7.3.118}\))\(mg\), ми маємо що: Для
   \[\gamma = \dfrac{T}{mg} - \dfrac{1}{E}.\]
   того,\(\gamma\) щоб бути максимальним:
   \(\bullet\)\(T = T_{\max, av} = 95510\ N\).
   \(\bullet\)\(E = E_{\max}\).
   Давайте тепер приступимо до виведення максимального аеродинамічного ККД:
   Аеродинамічний ККД визначається як:
   \[E = \dfrac{L}{D} = \dfrac{C_L}{C_D}.\label{eq7.3.125}\]
   Підставляючи параболічну полярну криву, наведену в твердженні в Equation (\(\ref{eq7.3.125}\)), ми отримати: Для
   \[E = \dfrac{C_L}{C_{D_0} + C_{D_i} C_L^2}.\label{eq7.3.126}\]
   того, щоб шукати значення, відповідні максимальному аеродинамічному ККД, потрібно вивести і зробити його рівним нулю, тобто:
   \[\dfrac{dE}{dC_L} = 0 = \dfrac{C_{D_0} - C_{D_i} C_L^2}{(C_{D_0} - C_{D_i} C_L^2)^2} \to (C_L)_{E_{\max}} = C_{L_{opt}} = \sqrt{\dfrac{C_{D_0}}{C_{D_i}}}.\label{eq7.3.127}\]
   Підставляючи значення\(C_{L_{opt}}\) в Рівняння (\(\ref{eq7.3.126}\)) і спрощення отримуємо, що:
   \[E_{\max} = \dfrac{1}{2\sqrt{C_{D_0} C_{D_i}}}.\nonumber\]
   Підставляючи:\(C_{L_{opt}} = 0.8, E_{\max} = 16.66\), і\(\gamma_{\max} = 5.27^{\circ}\).
   Аеродинамічна швидкість буде задаватися за допомогою:
   \[V = \sqrt{\dfrac{m \cdot g}{\tfrac{1}{2} \rho S_w C_{L_{opt}}}} = 119\ m/s.\nonumber\]
   From Equation (\(\ref{eq7.3.117}\)),\(\dot{h}_e = V \cdot \gamma = 10.95\ m/s\).
3. Ми хочемо виконувати горизонтальний поворот на висоті\(h = 0\) з коефіцієнтом навантаження\(n = 2.5 = n_{\max}\), і зі швидкістю, відповідною максимальній аеродинамічній ефективності при горизонтальному, стійкому, прямому польоті.
   Рівняння, що регулюють динаміку літака в горизонтальному повороті, такі:
   \[T = D;\label{eq7.3.128}\]
   \[mV \dot{\chi} = L \sin \mu;\label{eq7.3.129}\]
   \[L \cos \mu = mg.\label{eq7.3.130}\]
   При рівномірному (нерухомому) круговому русі добре відомо, що тангенціальна швидкість дорівнює кутовій швидкості,\(\dot{\chi}\) помноженій на радіус повороту\(R\):
   \[V = \dot{\chi} R.\]
   Отже\(\ref{eq7.3.128}\), System (\(\ref{eq7.3.129}\),,\(\ref{eq7.3.130}\)) можна переписати як:
   \[T = D;\label{eq7.3.132}\]
   \[n \sin \mu = \dfrac{V^2}{gR};\label{eq7.3.133}\]
   \[n = \dfrac{1}{\cos \mu};\label{eq7.3.134}\]
   де\(n = \tfrac{L}{mg}\) - коефіцієнт навантаження.
   (а). Необхідний кут банку:
   Тому, дивлячись на Рівняння (\(\ref{eq7.3.134}\)), легко визначити, що кут повороту банку є\(\mu = 66.4^{\circ}\).
   (б). Швидкість і радіус повороту.
   Для початку нам потрібно c розрахувати швидкість, відповідну максимальному ККД. Як ми розраховували раніше в Equation (\(\ref{eq7.3.127}\)), коефіцієнт підйому, який генерує максимальну ефективність, є так званим оптимальним коефіцієнтом підйому, тобто\(C_{L_{opt}} = \sqrt{\tfrac{C_{D_0}}{C_{D_i}}} = 0.8\). Потім швидкість дає:
   \[V = \sqrt{\dfrac{L}{\tfrac{1}{2} \rho_0 S_w C_{L_{opt}}}} = 161.57\ m/s.\nonumber\]
   Введення в рівняння (\(\ref{eq7.3.133}\)) з\(\mu = 66.4\) [град] і\(V = 161.57\ m/s\);\(R = 1167\ m\).
   (в) Необхідна тяга.
   Рівняння (\(\ref{eq7.3.132}\)) можна виразити так:
   \[T = \dfrac{1}{2} \rho_0 S_w V^2 C_{D_0} + \dfrac{L^2}{\tfrac{1}{2} \rho_0 V^2 S_w} C_{D_i}.\nonumber\]
   Оскільки всі значення відомі:\(T = 94093\ N\)
   (d). Так як\(T \le T_{\max, av} (h = 0)\), літак може виконувати поворот.

---

9. Всі ці змінні можна вважати постійними під час зльоту.

10. Зверніть увагу, що, враховуючи висоту та налаштування тяги, літак теоретично може літати з двома різними швидкостями, тим часом ці швидкості лежать між мінімальною швидкістю (стійло) та максимальною швидкістю (зазвичай поблизу швидкості розбіжності).

11. \(g\)являє собою силу, обумовлену гравітацією.

12. Зверніть увагу, що ми можемо перетворити масу у вагу, просто помноживши на силу тяжіння.

13. Зверніть увагу, що, враховуючи висоту та налаштування тяги, літак теоретично може літати з двома різними швидкостями, тим часом ці швидкості лежать між мінімальною швидкістю (стійло) та максимальною швидкістю (зазвичай поблизу швидкості розбіжності).

14. Це стосується значення від 0 до 1, пов'язаного з положенням рівня дросельної заслінки.